MongDB 的安装

1 安装 MongDB

---

https://www.mongodb.com/try/download/community-kubernetes-operator

• 这里我们选择 ZIP

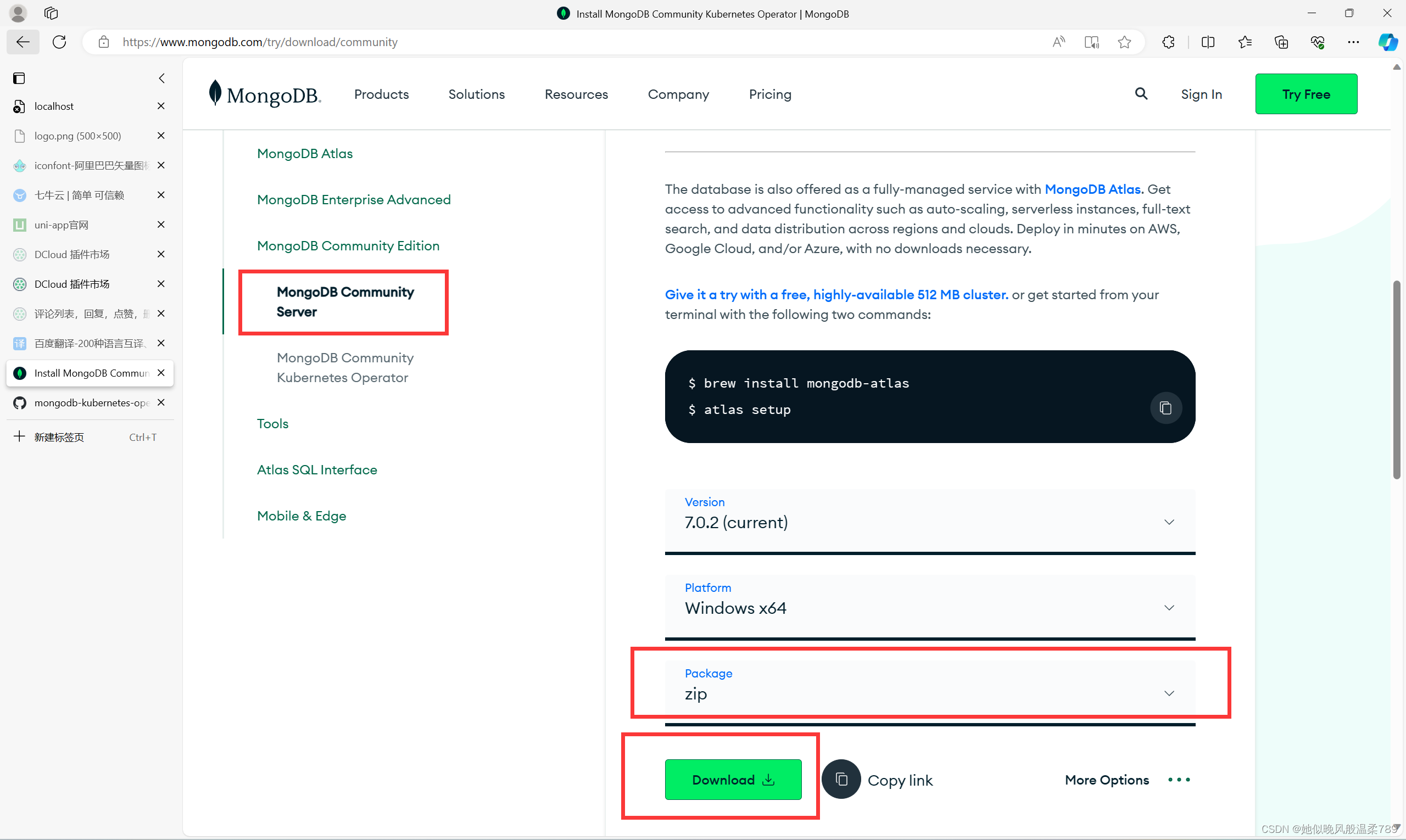
• 解压到文件夹

• 创建 data 文件

• 在 data 文件夹里面创建 db 和 logs 文件夹

• 进入 bin 目录 输入 cmd 回车

2 启动 MongDB

---

• 输入启动命令

mongod --dbpath=..\data\db

mongod --dbpath=…\data\db

• 这里可以看到我们的端口号和主机名

• 输出 logs 文件 (按 Ctrl + C 停止后输入下面命令)

mongod --logpath=…\data\logs\mongodb.log

mongod --logpath=..\data\logs\mongodb.log

3 配置环境变量

---

• 操作步骤：
  • 此电脑 > 右击 > 属性 > 高级系统设置

• 操作步骤
  • 环境变量 > Path(系统环境变量) > 新建 > 浏览 > 找到 MongDB 的bin 目录

• 测试 F:\IDEACODE\MongDB\mongodb-win32-x86_64-windows-7.0.2\data\db 替换成自己的路径

mongod --dbpath=F:\IDEACODE\MongDB\mongodb-win32-x86_64-windows-7.0.2\data\db

mongod --dbpath=F:\IDEACODE\MongDB\mongodb-win32-x86_64-windows-7.0.2\data\db