1. 线性可分支持向量机
1.1 定义输入数据
假设给定⼀个特征空间上的训练集为:
![]()
![]()
其中,(x , y )称为样本点。 x 为第i个实例(样本)。
y 为x 的标记: 当y = 1时,x 为正例;当y = −1时,x 为负例
正负用(-1,1)表示的原因:最大的作用就是标记,你也可以⽤(2,-3)来标记。只是为了⽅便,y
/y = y ∗ y 的过程中刚好可以相等,便于之后的计算。)
1.2 最大间隔
给定了上⾯提出的线性可分训练数据集,通过间隔最大化得到分离超平面为![]()
相应的分类决策函数为: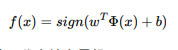
以上决策函数就称为线性可分⽀持向量机。 Φ(x)是某个确定的特征空间转换函数,它的作⽤是将x
映射到更高的维度,它有⼀个以后我们经常会见到的专有称号"核函数"。
比如我们看到的特征有2个: x1, x2,组成最先见到的线性函数可以是w1x1 + w2x2。但也许这
两个特征并不能很好地描述数据,于是我们进行维度的转化,变成了 w1x1 + w2x2 + w3x1x2+
w4x^2 + w5x^2。于是我们多了三个特征。⽽这个就是笼统地描述x的映射的。 最简单直接的就
是:Φ(x) = x。
我们要去求出这样⼀个超平面y(x),它能够最优地分离两个集合。 其实也就是我们要去求⼀组
参数(w,b),使其构建的超平面函数能够最优地分离两个集合。
如下就是⼀个最优超平面:
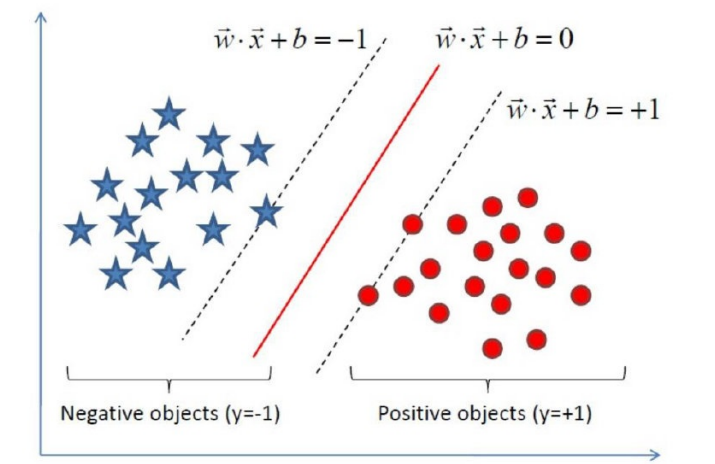
1.3 推到目标函数
超平面表达式:![]() 为了方便我们让:
为了方便我们让:![]()
则在样本空间中,划分超平面可通过如下线性方程来描述:![]()
其中,![]() 为法向量,决定了超平面的方向;
为法向量,决定了超平面的方向;
b为位移项,决定了超平面和原点之间的距离。
显然,划分超平面可被法向量w和位移b确定,我们把其记为(w,b)。
样本空间中任意点x到超平面(w,b)的距离可写成: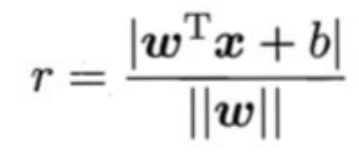
假设超平面(w, b)能将训练样本正确分类,即对于(x , y ) ∈ D。
令: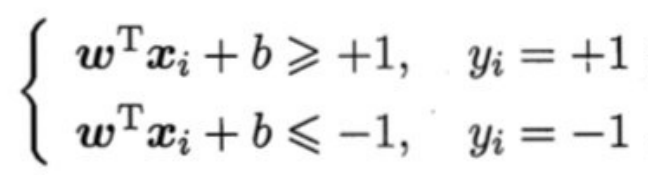
如图所示,距离超平面最近的几个训练样本点使上式等号成立,他们被称为“支持向量"。
两个异类支持向量到超平面的距离之和为:![]()
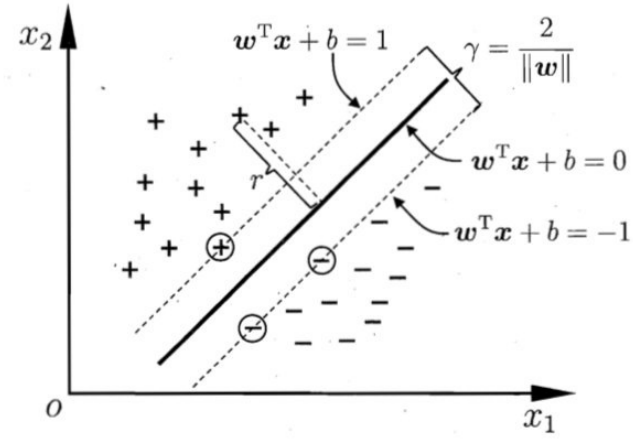
欲找到具有最⼤间隔的划分超平面,也就是要找到能满足下式中约束的参数w和b,使得γ最大。
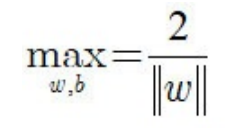
![]()
显然,为了最⼤化间隔,仅需要最大化:![]() ,这等价于最小化
,这等价于最小化![]() 。
。
于是上式可以重写为:![]()
![]() 。
。
PS:||W||是向量与矩阵的范数。
1.4 目标函数的求解
因为目标函数带有⼀个约束条件,所以我们可以用拉格朗日乘子法求解。
拉格朗日乘子法 (Lagrange multipliers)是⼀种寻找多元函数在⼀组约束下的极值的方法。
通过引入拉格朗日乘子,可将有 d 个变量与 k 个约束条件的最优化问题转化为具有 d + k 个变量的
无约束优化问题求解。
经过朗格朗日乘子法,我们可以把目标函数转换为:
![]()
其中,要想求得极小值,上式后半部分:
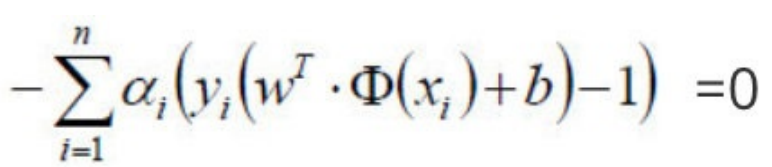
走到这⼀步,这个目标函数还是不能开始求解,现在我们的问题是极小极大值问题 。
我们要将其转换为对偶问题,变成极⼤极小值问题:![]()
⾸先我们对原目标函数的w和b分别求导:
原函数为:![]()
对w求偏导:![]()
对b求偏导: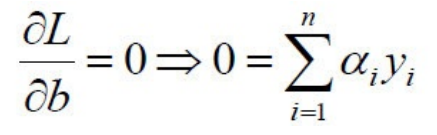
然后将以上w和b的求导函数重新代⼊原目标函数的w和b中,得到的就是原函数的对偶函数:

于是现在要求的是这个函数的极大值max(a),写成公式就是:
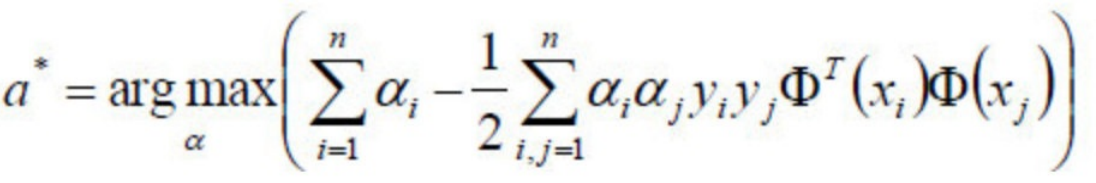
好了,现在我们只需要对上式求出极⼤值α,然后将α代⼊w求偏导的那个公式:![]()
从而求出w。将w代⼊超平面的表达式,计算b值;现在的w,b就是我们要寻找的最优超平面的参数。
2. 线性不可分支持向量机
2.1 线性不可分的情况
我们可以为分错的点加上一点惩罚,对一个分错的点的惩罚函数就是这个点到其正确位置的距离:
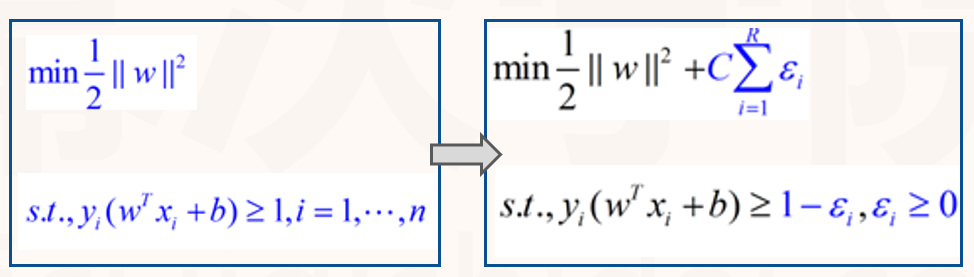
C是一个由用户去指定的系数,表示对分错的点加入多少的惩罚,当C很大的时候,分错的点
就会更少,但是过拟合的情况可能会比较严重,当C很小的时候,分错的点可能会很多,不过可能
由此得到的模型也会不太正确 。
软支持向量机求解:
构造拉格朗日公式:
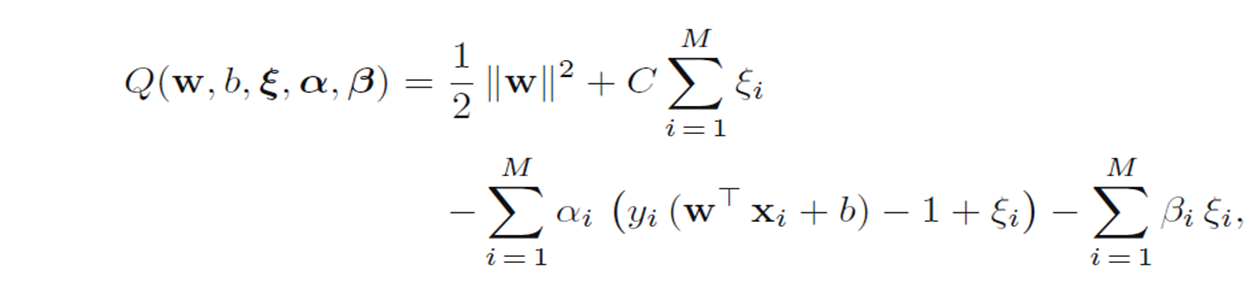
求偏导数:
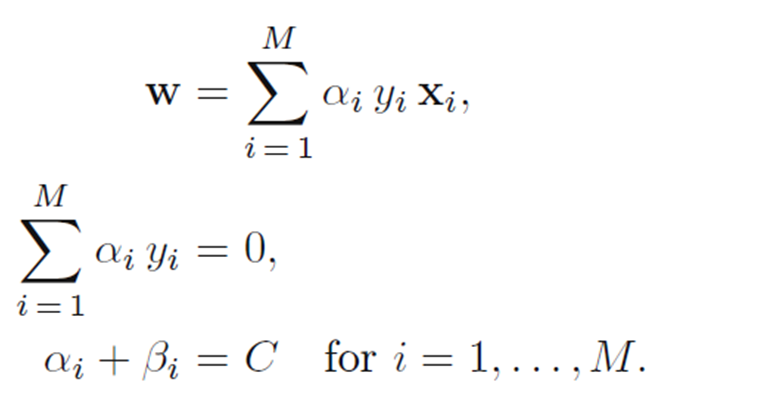
转为对偶函数求解。
实际上在处理大型问题时,由于存储和计算两方面的要求,这些算法往往会失效。
2.2 坐标上升法
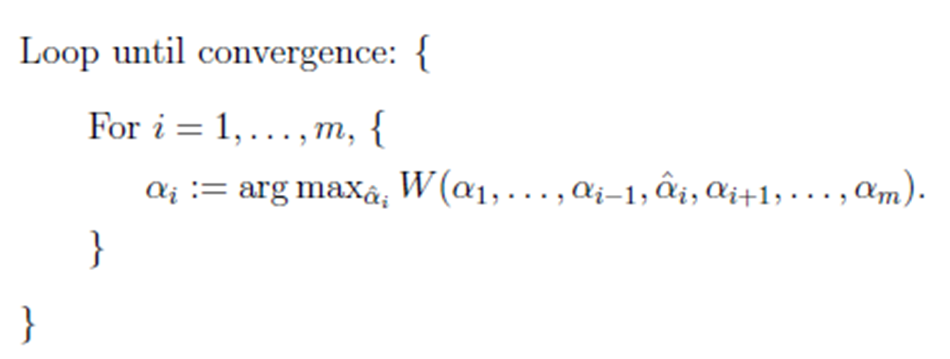
固定除 αi 之外的所有参数,这时W可看作只是关于 αi 的函数,那么直接对 αi 求导优化即
可。可以通过更改优化顺序来使W能够更快地增加并收敛。如果W在内循环中能够很快地达到最
优,那么坐标上升法会是一个很高效的求极值方法。
固定以外的所有参数,那么将不再是变量(可以由其他值推出),因为问题中规定了
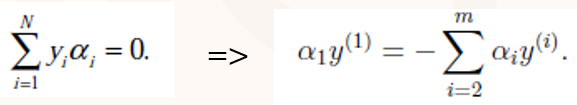
因此,我们最少一次需要选取两个参数做优化,比如αi和αj,此时可以由和其他参数表示出来。
3. SMO算法
3.1 SVM算法特点
SVM有如下主要几个特点:(1)非线性映射是SVM方法的理论基础,SVM利用内积核函数代替
向高维空间的非线性映射;(2)对特征空间划分的最优超平面是SVM的目标,最大化分类边际的思想
是SVM方法的核心;(3)支持向量是SVM的训练结果,在SVM分类决策中起决定作用的是支持向量。
因此,模型需要存储空间小,算法鲁棒性强;(4)无序任何前提假设,不涉及概率测度。
SVM有如下主要几个缺点:(1) SVM算法对大规模训练样本难以实施由于SVM是借助二次规
划来求解支持向量,而求解二次规划将涉及m阶矩阵的计算(m为样本的个数),当m数目很大时
该矩阵的存储和计算将耗费大量的机器内存和运算时间。针对以上问题的主要改进有有J.Platt的
SMO算法、T.Joachims的SVM、C.J.C.Burges等的PCGC、张学工的CSVM以及O.L.Mangasarian
等的SOR算法;(2) 用SVM解决多分类问题存在困难经典的支持向量机算法只给出了二类分类的算
法,而在数据挖掘的实际应用中,一般要解决多类的分类问题。可以通过多个二类支持向量机的组
合来解决。主要有一对多组合模式、一对一组合模式和SVM决策树;再就是通过构造多个分类器
的组合来解决。主要原理是克服SVM固有的缺点,结合其他算法的优势,解决多类问题的分类精
度。如:与粗集理论结合,形成一种优势互补的多类问题的组合分类器。
3.2 SMO算法
SMO算法由Microsoft Research的John C. Platt在1998年提出,并成为最快的二次规划优化算
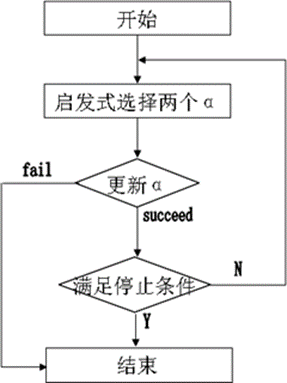
法,特别针对线性SVM和数据稀疏时性能更优。第一步选取一对参数,选取方法使用启发式方法
(Maximal violating pair)。第二步,固定除被选取的参数之外的其他参数,确定W极值。
假设我们选取了初始值满足了问题中的约束条件。接下来,我们固定其余参数,这样W就是
和的函数。并且和满足条件: 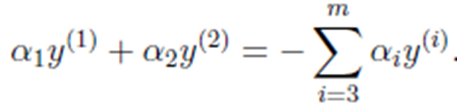
由于其余参数都是已知固定,因此为了方便,可将等式右边标记成实数值。
![]()
![]()
![]()
进而:![]()

目标函数:![]()
其中: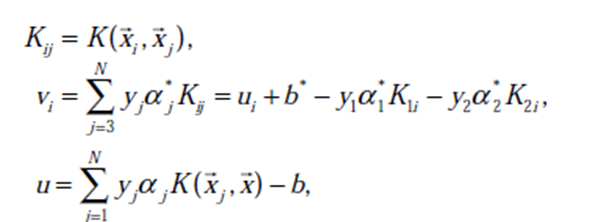
求偏导: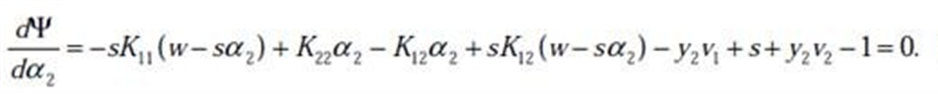
![]()
带入w, v:![]()
求得: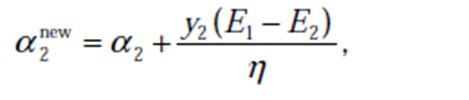
最终参数的解为:![]()
![]()
3.3 参数取值
当a1和a2异号时,也就是一个为1,一个为-1时,他们可以表示成一条直线,斜率为1。如下图:
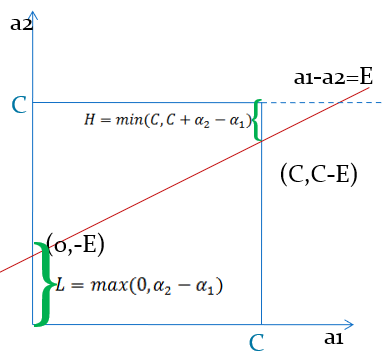
横轴是a2,纵轴是a1,a1和a2既要在矩形方框内,也要在直线上,因此
![]()
![]()
同理,当y1和y2同号时:
![]()
![]()
参数计算:![]()
![]()

b的求解:
设![]() 在界内,则
在界内,则![]()
![]()
有![]() ,代入上式得:
,代入上式得:
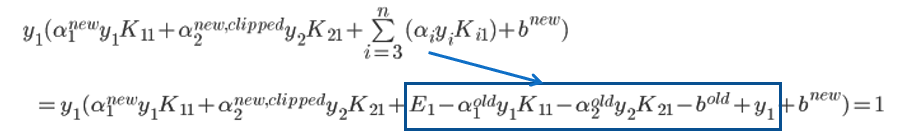
两边同乘以y1,得:
![]()
![]()
设![]() 在界内,则
在界内,则
![]()
![]()
![]() 在界内,则情况1和情况2的b值相等,任取一个;都不在界内,则
在界内,则情况1和情况2的b值相等,任取一个;都不在界内,则 ![]() 取值为
取值为
情况1和情况2之间的任意值。
3.4 算法终止条件
一个自然的想法是那些违反KKT最严重的点,他们对间距贡献最大,因此可以通过该启发规则
来完成调整参数的选取。(并且此种启发规则计算量小)
①停止条件1(满足KTT条件)

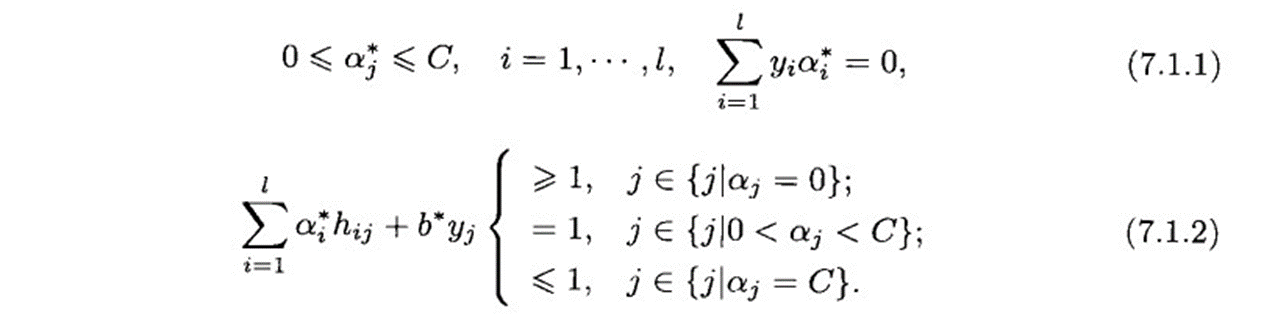
KTT条件:
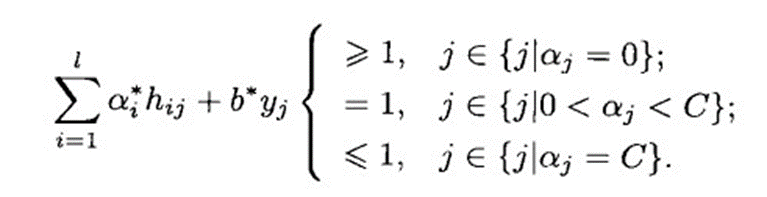 并设:
并设:![]()
代入得: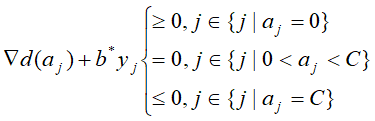 左移:
左移: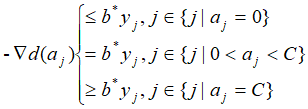
分别乘以yi:
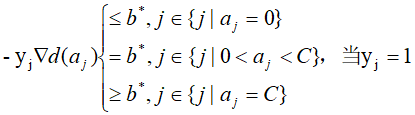
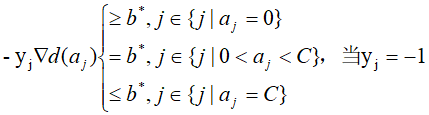
统一得到: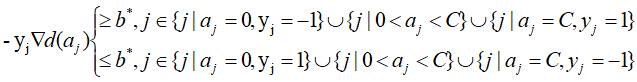
等价于: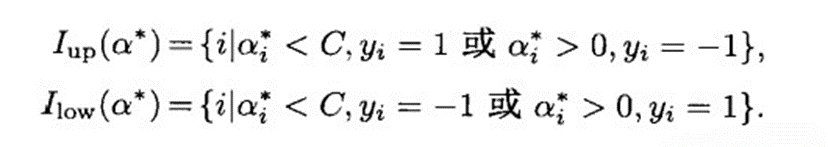

如果对于: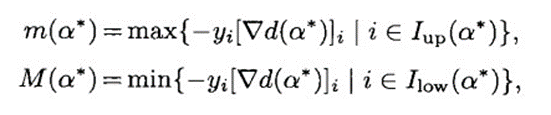 可以判断:
可以判断:![]()
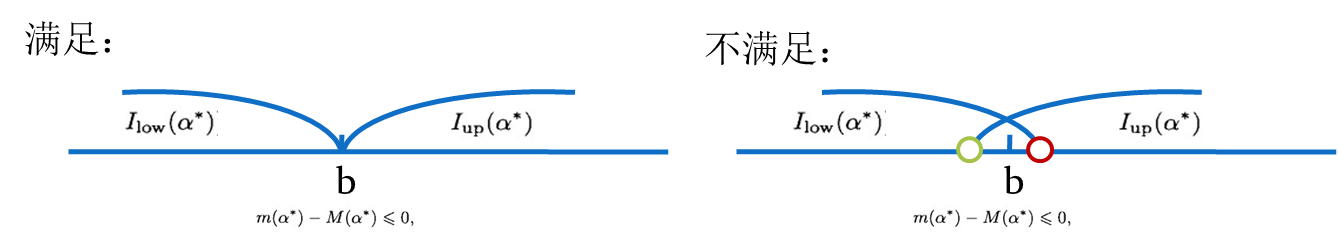 ②停止条件2
②停止条件2

③停止条件3
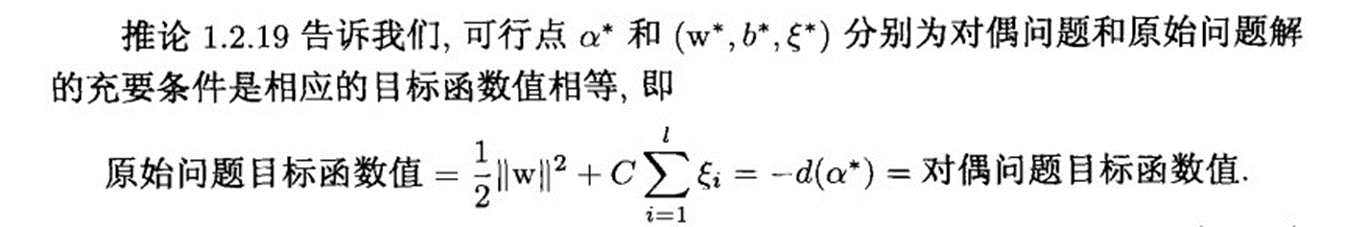
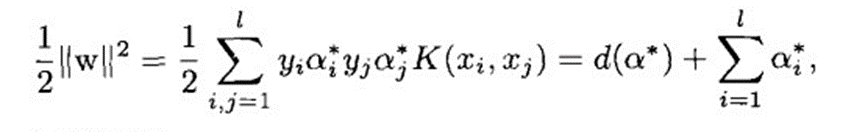

应该指出,检验停机准则的精度要求对算法的执行时间影响很大。过高的要求会非常浪费时
间,却不一定会改进决策函数。所以在实际应用中,我们要精心选择停机准则.
此外,上面停机准则的讨论也会给我们改进算法和提高算法的效率提供一些启发,比如在迭代过程
中可以特别注意那些违背停机准则“最严重”的训练点。

其他的求解方法:
选块算法:

分解算法:

工作集的选取:










)


![[PyTorch][chapter 59][强化学习-2-有模型学习]](http://pic.xiahunao.cn/[PyTorch][chapter 59][强化学习-2-有模型学习])






