[PyTorch][chapter 59][强化学习-2-有模型学习]

前言：

在已知模型的环境里面学习,称为有模型学习（model-based learning）.

此刻,下列参数是已知的：

$p_{x\rightarrow x^{'}}^{a}$ : 在状态x 下面,执行动作a ,转移到状态 $x^{'}$ 的概率

$R_{x\rightarrow x^{'}}^a$ : 在状态x 下面,执行动作a ,转移到 $x^{'}$ 的奖赏

有模型强化学习的应用案例
棋类游戏：有模型强化学习算法（例如MCTS）被广泛应用于棋类游戏，例如围棋、国际象棋等。AlphaGo和AlphaZero就是使用MCTS的典型例子。

路径规划：有模型强化学习算法（例如动态规划）可以用于路径规划问题，例如机器人导航、无人机路径规划等。

资源调度：有模型强化学习算法可以用于优化资源调度问题，例如数据中心的任务调度、物流配送的路径规划等

策略评估
Bellman Equation
基于 T步累积奖赏的策略评估算法例子

一策略评估

模型已知时,对于任意策略 $\pi$ ,能估算出该策略带来的期望累积奖赏。

假设：

状态值函数： $V^{\pi}(x)$ : 从状态x 出发,使用策略 $\pi$ ,带来的累积奖赏

状态-动作值函数 $Q^{\pi}(x,a)$ : 从状态x 出发,执行动作a,再使用策略 $\pi$ ,带来的累积奖赏

由定义:

状态值函数为：

$V_{T}^{\pi}(x)=E_{\pi}[\frac{1}{T}\sum_{t=1}^Tr_t|x_0=x]$ : T 步累积奖赏

$V_{\gamma}^{T}(x)=E_{\pi}[\frac{1}{T}\sum_{t=0}^T \gamma^tr_{t+1}|x_0=x]$ : $\gamma$ 折扣累积奖赏， $\gamma \in (0,1]$

状态-动作值函数

$Q_{T}^{\pi}(x,a)=E_{\pi}[\frac{1}{T}\sum_{t=1}^Tr_t|x_0=x,a_0=a]$ T 步累积奖赏

$Q_{\gamma}^{T}(x,a)=E_{\pi}[\frac{1}{T}\sum_{t=0}^T \gamma^tr_{t+1}|x_0=x,a_0=a]$ $\gamma$ 折扣累积奖赏

由于MDP具有马尔可夫性，即现在决定未来，将来和过去无关，我们很容易找到值函数的递归关系（Bellman 等式）

$V_{T}^{\pi}(x)=E_{\pi}[\frac{1}{T}\sum_{t=1}^T r_t|x_0=x]$

$=E_{\pi}[\frac{1}{T}r_1+\frac{T-1}{T}\frac{1}{T-1}\sum_{t=2}^T r_t|x_0=x]$

$=\sum_{a \in A} \pi(x,a) \sum _{x^{'} \in X}P_{x\rightarrow x^{'}}^a (\frac{1}{T}R_{x\rightarrow x^{'}}^{a}+\frac{T-1}{T}E_{\pi}[\frac{1}{T-1}\sum_{t=1}^{T-1}r_t|x_0=x^{'}])$

$=\sum_{a \in A}\pi (x,a) \sum_{x^{'} \in X} P_{x\rightarrow x^{'}}^a(\frac{1}{T} R_{x \rightarrow x^{'}}^a+\frac{T-1}{T}V_{T-1}^{\pi}(x^{'}))$

2.2 r折扣累积奖赏

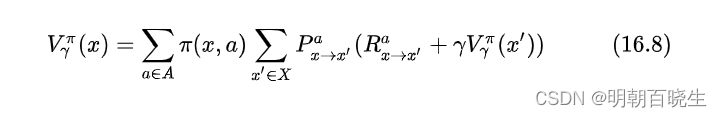
这是一种动态规划方案,从 $V_{0}^{\pi}$ 出发，通过一次迭代就能计算出每个状态的单步累积奖赏

$V_{1}^{\pi}$

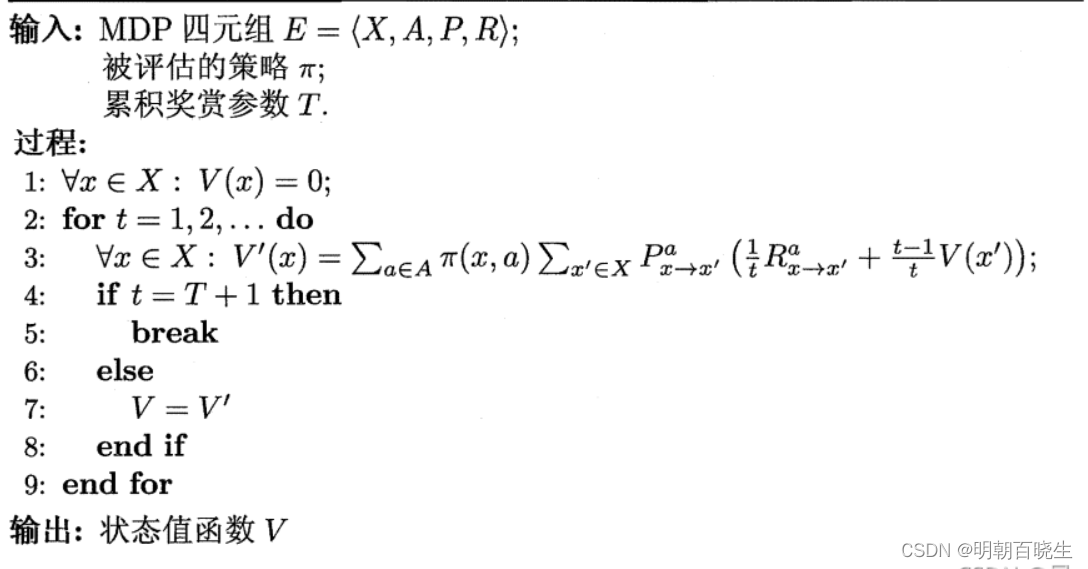
有了状态值函数V后，可以直接计算出状态-动作值函数：

由于算法可能会迭代很多次,可以设置一个阀值，当执行一次迭代后

函数值小于 $\delta$ ，停止迭代

$max_{x \in X}|V(x)-V^{'}(x)|<\delta$

二 Bellman Equation（贝尔曼方程）

2.1 Summing all future rewards and discounting them would lead to our return G

$G_t= R_{t+1}+\gamma R_{t+2}+r^2 R_{t+3}+..., \gamma \in (0,1)$

2.2 state-value function

给定策略 $\pi$ 时，基于 state s 的条件期望函数，公式表示为：

$v_{\pi}=E(G_t|S_t=s)$

State-value function can be broken into:

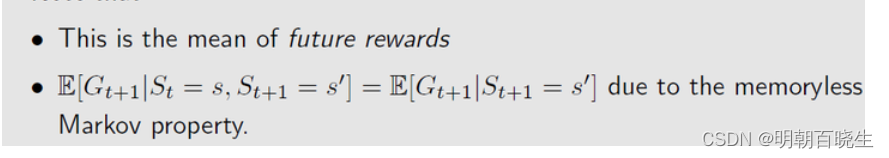
三基于 T步累积奖赏的策略评估算法例子

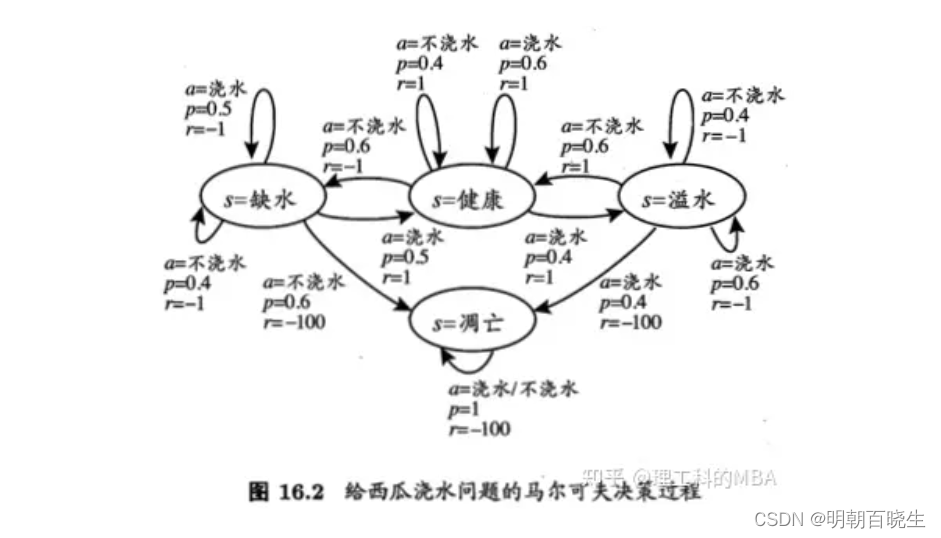
代码里面的行为函数采用的是Stochastic

# -*- coding: utf-8 -*-
"""
Created on Mon Oct 30 15:38:17 2023@author: chengxf2
"""
import numpy as np
from enum import Enumclass State(Enum):#状态空间X    shortWater =1 #缺水health = 2  #健康overflow = 3 #凋亡apoptosis = 4 #溢水class Action(Enum):#动作空间Awater = 1 #浇水noWater = 2 #不浇水class Env():def __init__(self):#状态空间self.X = [State.shortWater, State.health,State.overflow, State.apoptosis]   #动作空间self.A = [Action.water,Action.noWater]   self.Q ={}#从状态x出发,执行动作a,转移到新的状态x'，得到的奖赏 r为已知道self.Q[State.shortWater] =[[Action.water,0.5,   State.shortWater,-1],[Action.water,0.5,   State.health,1],[Action.noWater,0.4, State.shortWater,1],[Action.noWater,0.6, State.overflow,-100]]self.Q[State.health]      =         [[Action.water,0.6,   State.health,1],[Action.water,0.4,   State.apoptosis,-1],[Action.noWater,0.6, State.shortWater,-1],[Action.noWater,0.4, State.health,1]]self.Q[State.overflow] =  [[Action.water,0.6,   State.overflow,-1],[Action.water,0.4,   State.apoptosis,-100],[Action.noWater,0.6, State.health,1],[Action.noWater,0.4, State.overflow,-1]]self.Q[State.apoptosis] =[[Action.water,1, State.apoptosis,-100],[Action.noWater,1, State.apoptosis,-100]]def GetX(self):#获取状态空间return self.Xdef GetAction(self):#获取动作空间return self.Adef GetQTabel(self):return self.Qclass LearningAgent():def GetStrategy(self):   #策略,处于不同的状态下面,采用不同的actionstragegy ={}stragegy[State.shortWater] = {Action.water:1.0, Action.noWater:0.0}stragegy[State.health] =    {Action.water:0.9, Action.noWater:0.1}stragegy[State.overflow] = {Action.water:0.1, Action.noWater:0.9}stragegy[State.apoptosis] = {Action.water:0.0, Action.noWater:0.0}return stragegydef __init__(self):env = Env()self.X = env.GetX()self.A = env.GetAction()self.QTabel = env.GetQTabel()self.curV ={} #前面的累积奖赏self.V ={} #累积奖赏for x in self.X:    self.V[x] =0self.curV[x]=0def GetAccRwd(self,state,stragegy,t,V):#AccumulatedRewards#处于x状态下面，使用策略，带来的累积奖赏reward_x  =0.0for action in self.A:#当前状态处于x,按照策略PI,选择action 的概率,正常为1个,也可以是多个（按照概率选取对应的概率)p_xa = stragegy[state][action] # 使用策略选择action 的概率#任意x' in  X, s下个状态QTabel= self.QTabel[state]reward =0.0#print("\n ---Q----\n",QTabel)for Q in QTabel:#print(Q, action)if Q[0] == action:#新的状态x'newstate = Q[2] #当前状态x,执行动作a,转移到新的状态s的概率p_a_xs =   Q[1]#当前状态x,执行动作a,转移到新的状态s,得到的奖赏r_a_xs = Q[-1]reward += p_a_xs*((1.0/t)*r_a_xs + (1.0-1/t)*V[newstate])#print("\n 当前状态 ",x, "\t 转移状态 ",s, "\t 奖赏 ",r_a_xs,"\t 转移概率 ",p_a_xs ,"\t reward",reward)reward_x +=p_xa*rewardreturn reward_xdef learn(self,T):stragegy =  self.GetStrategy()for  t  in range(1,T+1):#获得当前的累积奖赏for x in self.X:self.curV[x] = self.GetAccRwd(x,stragegy,t,self.V)if (T+1) == t:breakelse:self.V = self.curVfor x in self.X:print("\n 状态 ",x, "\t 奖赏 ",self.V[x])if __name__ == "__main__":T =100agent = LearningAgent()agent.learn(T)

参考：

https://www.cnblogs.com/CJT-blog/p/10281396.html

1. 有模型强化学习概念理解_哔哩哔哩_bilibili

1.强化学习简介_哔哩哔哩_bilibili

16 强化学习 - 16.3 有模型学习 - 《周志华《机器学习》学习笔记》 - 书栈网 · BookStack

1 强化学习基础-Bellman Equation - 知乎

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/131687.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！