今天讲一下倍增
目录
题目:忠诚
思路:
题目:国旗计划
思路:
查询迭代类倍增:
本质是一个一个选区间使总长度达到 M,类似凑一个数。而我们会经常用不大于它最大的二的次幂,减去之后,再重复这个过程,这样这个数的值会减小得非常快,一共只需要减 log(num) 次就可以凑出。
题目:忠诚


思路:
很明显是一道区间最值的问题:也就是著名的RMQ(Range Minimum/Maximum Query)区间最值查询问题(最好会背啊!)
首先设置f[i][j]表示从下标i走2*j长度之间的最值,然后依此创建ST表,最后RMQ查询ST表即可
#include<bits/stdc++.h>
using namespace std;
#define maxn 100005
int n,m,l,r,a[maxn],f[maxn][22]; //f[i][j](ST表)表示从下标i走2*j长度之间的最值
int RMQ(int l,int r)//RMQ(Range Minimum/Maximum Query)区间最值查询
{int k=log2(r-l+1);return min(f[l][k],f[r-(1<<k)+1][k]);
}
void ST_create(){//创建ST表for(int i=1;i<=n;i++) f[i][0]=a[i];//初始化int k=log2(n);for(int j=1;j<=k;j++){//(0已经初始化过了) j是二进制大小for(int i=1;i<=n-(1<<j)+1;i++){//对每个点遍历 ,n要减去j的枚举范围:n-2^j+1f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1]);//递推公式}}
}
int main()
{scanf("%d%d",&n,&m);//账数和问题数for(int i=1;i<=n;i++) scanf("%d",&a[i]);ST_create();for(int i=1;i<=m;i++){scanf("%d%d",&l,&r);printf("%d ",RMQ(l,r));}return 0;
}
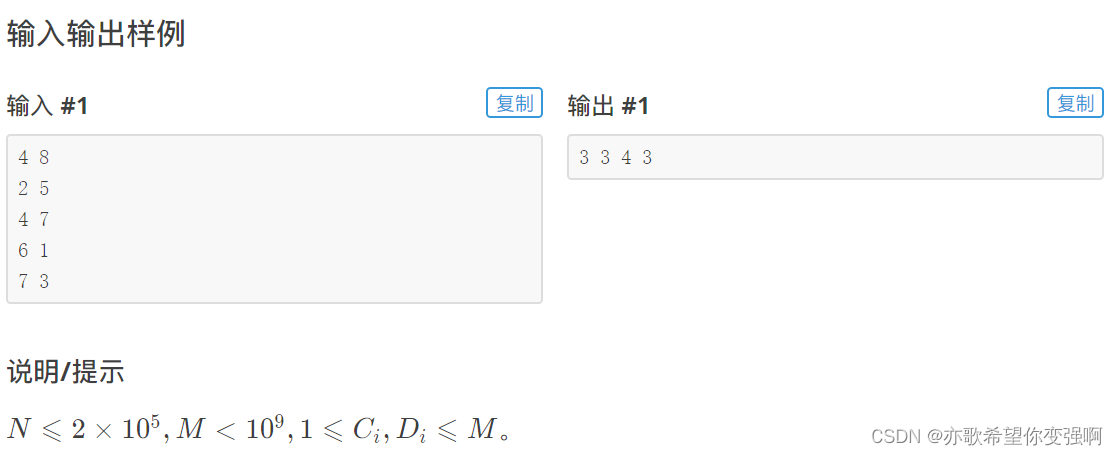
题目:国旗计划

思路:
求f[i][0]:即每个区间后选的第一个区间。肯定不能两重循环,那时间复杂度就再次变为 O(N^2),这个时候利用题目中提到的一个性质:
“每名边防战士的奔袭区间都不会被其他边防战士的奔袭区间所包含 ”
则对于单调递增l的, r也单调递增,我们只需要找到满足j.l<=r.i 的最后一个区间即可,因此使用双指针,时间复杂度降为 O(N)。
#include<bits/stdc++.h> //国旗计划(环形线段覆盖)(注意线段不会包含)
using namespace std;
#define ll long long
const int N=2e5+10;
int n,m,ans[N];
int st[20][N<<1],s[20][N<<1];//st[i][j]表示从j点为起点的进行2^i次迭代的起点的下标(自身不算)
struct segment{int l,r,id;inline friend bool operator<(const segment &a,const segment &b){return a.l<b.l; //因为线段不会包含,所以l越大自然r越大,即l单增则r单增 !!!}
}a[N<<1]; //把环表转换成两倍周长的线性表
void ST_create(){for(int i=1,j=1;i<=2*n;i++){while(j<=2*n&&a[j].l<=a[i].r) j++;//寻找下一个起点st[0][i]=j-1; //初始化}for(int i=1;i<=19;i++) //i是二进制大小for(int j=1;j<=2*n;j++) //j是对每个点遍历st[i][j]=st[i-1][st[i-1][j]];//状态转移方程
}
void search(){for(int i=1;i<=n;i++){ int up=a[i].l+m,an=0,p=i;//对每个点拆环范围为链范围for(int j=19;j>=0;j--)if(st[j][p]&&a[st[j][p]].r<up) //逼近过程an+=1<<j,p=st[j][p]; //从下一个点开始逼近ans[a[i].id]=an+2;//因为本来就没算本身,然后也不算入终点,所以加2}
}
int main(){cin>>n>>m; int l,r; //n是边防战士数,m是边防站数for(int i=1;i<=n;i++){scanf("%d %d",&l,&r);if(l>r) r+=m;//破环成链(对战士的覆盖范围)a[i].l=l,a[i].r=r,a[i].id=i;//每个战士的编号}sort(a+1,a+n+1); //方便初始时找下一个转移点for(int i=1;i<=n;i++) {a[i+n].l=a[i].l+m,a[i+n].r=a[i].r+m; //破环成链(对链边界上每个边防站士都再点缀一下)}ST_create(); //创建ST表search(); //对每个点进行查询for(int i=1;i<=n;i++)printf("%d ",ans[i]);return 0;
}可以总结一下倍增使用的场合:
1.(最值类)RMQ区间最值
2.(迭代类)同一件事完成多次。且当“一次做一件事”可以优化为“一次做多件事”。(快速幂也是这个道理)
双指针扫描的应用:
两个指针代表的内容均只增不减




![[自学记录08*]LDR、HDR与ToneMapping](https://img-blog.csdnimg.cn/4eb14a68616340a186d801650c81be20.png)