一、相似检索方法总体分析

相似检索方法是一种用于从大量数据中找到与查询数据相似的数据项的技术。这种方法通常用于信息检索、推荐系统、图像处理、自然语言处理等领域。相似检索主要方法可以总体分为以下几类：

基于距离度量的方法：

• 余弦相似度：测量向量之间的夹角，常用于文本和向量数据的相似性计算。
• 欧氏距离：测量向量之间的直线距离，适用于数值型数据。
• 曼哈顿距离：测量向量之间的城市街区距离，常用于多维数值数据。
• 汉明距离：用于度量二进制数据之间的相似性，例如，文档的二进制表示。

基于集合的方法：

• Jaccard相似度：用于度量两个集合的相似性，常用于集合数据、文档和推荐系统中。
• 杰卡德距离：度量两个集合之间的不相交性，是Jaccard相似度的互补度量。

基于内容的方法：

• 基于内容的相似检索使用数据的内容特征来计算相似性，如文本、图像、音频特征。它可以通过特征提取和向量化来实现。

协同过滤方法：

• 基于用户的协同过滤：使用用户行为数据，如评分、点击、购买记录，找到用户之间的相似性，用于个性化推荐。
• 基于项目的协同过滤：使用项目属性和用户的互动数据，找到项目之间的相似性，也用于个性化推荐。

基于图的方法：

• 基于图的相似检索用于在图数据库和社交网络中找到节点之间的相似性。它可以基于节点的连接和属性进行相似性计算。

基于深度学习的方法：

• 使用深度学习技术，如卷积神经网络 (CNN)、循环神经网络 (RNN) 和注意力机制来学习数据的表示和特征，然后计算相似性。

这些方法各自有其适用的场景和特点，选择合适的相似检索方法取决于应用的需求、数据类型和性能要求。通常，研究和实践中会根据具体情况采用不同的方法或它们的组合来解决相似检索问题。

二、基于距离度量的方法

（一）余弦相似度

余弦相似度是一种常用的相似性度量方法，特别适用于文本、向量和高维数据的相似性计算。它基于向量的夹角来度量两个向量之间的相似性，值的范围在-1到1之间。余弦相似度的计算公式如下：

余弦相似度（Cosine Similarity）= (A · B) / (||A|| * ||B||)

其中：

• A 和 B 是两个向量。
• A · B 表示向量 A 和向量 B 的点积（内积）。
• ||A|| 表示向量 A 的模（范数）。
• ||B|| 表示向量 B 的模。

余弦相似度的原理可以解释如下：

1. 余弦相似度度量的是两个向量之间的夹角，而不是它们的大小。如果两个向量指向相同方向，夹角为0度，余弦相似度为1，表示它们非常相似。如果夹角为90度，余弦相似度为0，表示它们无关或不相似。如果夹角为180度，余弦相似度为-1，表示它们方向完全相反。

2. 余弦相似度不受向量的绝对大小影响，只受其方向影响。这使得它在处理文本数据或高维数据时非常有用，因为文本的长度可能不同，但重要的是它们的方向，即词语的相对重要性。

3. 余弦相似度范围在-1到1之间，越接近1表示越相似，越接近-1表示越不相似，0表示中等相似度。

4. 余弦相似度适用于各种数据类型，包括文本、图像、向量等。在文本相似性计算中，通常使用词频或TF-IDF来表示文本数据的向量，然后使用余弦相似度来比较文本之间的相似性。

当使用余弦相似度来计算文本相似性时，可以考虑以下案例，其中有两个文本文档 A 和 B，我们要计算它们之间的相似性。

文档 A: "Machine learning is a subset of artificial intelligence that focuses on developing algorithms and models that enable computers to learn from and make predictions or decisions based on data."

文档 B: "Artificial intelligence encompasses a wide range of technologies, and machine learning is one of its key components, allowing computers to learn from data and make predictions."

首先，我们需要将这两个文档表示为向量。一种常见的表示方法是使用词频向量（Term Frequency, TF）或者 TF-IDF 向量（Term Frequency-Inverse Document Frequency）。在这里，我们使用 TF 向量来示范。

假设我们使用一个词汇表来表示文档 A 和 B，该词汇表包含以下词汇：["Machine", "learning", "artificial", "intelligence", "algorithms", "models", "data", "predictions", "computers"]。

接下来，我们计算文档 A 和 B 中每个词汇的词频。对于文档 A，我们有：

• "Machine": 1
• "learning": 1
• "artificial": 1
• "intelligence": 1
• "algorithms": 1
• "models": 1
• "data": 1
• "predictions": 1
• "computers": 1

对于文档 B，我们有：

• "Machine": 0
• "learning": 1
• "artificial": 1
• "intelligence": 1
• "algorithms": 0
• "models": 1
• "data": 1
• "predictions": 1
• "computers": 1

现在，我们可以将这两个文档表示为向量，其中每个元素表示相应词汇的词频。文档 A 的向量是 [1, 1, 1, 1, 1, 1, 1, 1, 1]，文档 B 的向量是 [0, 1, 1, 1, 0, 1, 1, 1, 1]。

接下来，我们计算这两个向量的余弦相似度。使用余弦相似度公式：

余弦相似度 = (A · B) / (||A|| * ||B||)

其中，

• A · B 是向量 A 和向量 B 的点积：1 * 0 + 1 * 1 + 1 * 1 + 1 * 1 + 1 * 0 + 1 * 1 + 1 * 1 + 1 * 1 + 1 * 1 = 6
• ||A|| 是向量 A 的模（范数）：√(1^2 + 1^2 + 1^2 + 1^2 + 1^2 + 1^2 + 1^2 + 1^2 + 1^2) = √9 = 3
• ||B|| 是向量 B 的模（范数）：√(0^2 + 1^2 + 1^2 + 1^2 + 0^2 + 1^2 + 1^2 + 1^2 + 1^2) = √7

现在，我们可以计算余弦相似度：

余弦相似度 = (6) / (3 * √7) ≈ 0.612

余弦相似度的值约为0.612，表示文档 A 和文档 B 之间的相似度较高，因为它们共享了许多相同的词汇。这个案例说明了如何使用余弦相似度来量化文本文档之间的相似性，其中向量表示文档的词频信息。

（二）欧氏距离

欧氏距离（Euclidean Distance）是一种用于测量两个点在多维空间中的直线距离的距离度量方法。它是最常见和直观的距离度量方式，通常用于数值型数据或特征空间中。欧氏距离的原理可以如下解释：

假设有两个点 A 和 B，它们在二维空间中的坐标分别是 (x1, y1) 和 (x2, y2)。欧氏距离计算这两个点之间的距离，可以使用以下公式：

欧氏距离 = √((x2 - x1)² + (y2 - y1)²)

这个公式实际上是在计算点 A 到点 B 之间的直线距离。将这个概念推广到多维空间，如果有两个点 A 和 B，它们在 n 维空间中的坐标分别是 (x1, y1, z1, ..., wn) 和 (x2, y2, z2, ..., wn)，那么欧氏距离可以表示为：

欧氏距离 = √((x2 - x1)² + (y2 - y1)² + (z2 - z1)² + ... + (wn - w1)²)

欧氏距离的主要特点包括：

• 直观性：欧氏距离是直线距离，因此在几何上非常直观。它衡量了两点之间的"最短路径"距离。

• 各向同性：欧氏距离在各个维度上对数据的权重是相等的，即各个维度对距离的贡献是一致的。这意味着它适用于各个维度上的特征值的权重相等的情况。

• 敏感性：欧氏距离对离群点（outliers）非常敏感，即某个维度上的一个异常值可以对距离产生较大的影响。这是因为欧氏距离考虑了所有维度上的值。

案列理解：当使用欧氏距离进行相似度计算时，考虑一个简单的示例，假设我们有两个点 A 和 B，它们的坐标分别是 (2, 3) 和 (4, 7)。我们将使用欧氏距离来计算这两个点之间的距离。

点 A: (2, 3) 

点 B: (4, 7)

欧氏距离的计算公式如下：

欧氏距离 = √((x2 - x1)² + (y2 - y1)²)

在这个例子中，我们有：

x1 = 2, y1 = 3（对应点A的坐标）

x2 = 4, y2 = 7（对应点B的坐标）

现在，我们可以将这些值代入公式计算欧氏距离：

欧氏距离 = √((4 - 2)² + (7 - 3)²) = √(2² + 4²)  = √(4 + 16)  = √20  ≈ 4.47

所以，点 A 和点 B 之间的欧氏距离约为4.47。

这个示例说明了如何使用欧氏距离来测量两个点之间的直线距离。在多维空间中，欧氏距离的计算方法类似，只需要将每个维度的差值的平方相加，然后取平方根，即可计算出两点之间的欧氏距离。欧氏距离常用于聚类分析、距离度量、图像处理等各种领域，以评估数据点之间的相似性或差异。

用于商品推荐的实际案例：假设你是一家电子商务公司的数据分析师，你想根据用户的购买历史为他们推荐新的商品。你使用欧氏距离来计算用户之间的相似性，以便找到相似购买行为的用户，然后为他们推荐其他用户购买但他们尚未购买的商品。步骤：

1. 数据准备：你已经收集了用户的购买历史数据，其中每个用户被表示为一个特征向量，每个商品被表示为向量的一个维度。如果用户购买了商品，则该维度的值为1，否则为0。

2. 用户相似度计算：对于要推荐的用户，你计算他们与其他用户之间的欧氏距离。这表示为用户之间在购买历史上有多少相似的商品。

3. 相似用户选择：选择与目标用户距离最接近的若干用户，这些用户将被认为是潜在的相似用户。

4. 商品推荐：根据潜在相似用户的购买历史，为目标用户推荐他们尚未购买但相似用户已经购买的商品。

这个案例中，欧氏距离用于度量用户之间的相似性，以帮助为用户进行商品推荐。相似用户之间的欧氏距离越小，他们的购买历史越相似，从而更有可能对推荐产生积极反应。

这是一个实际应用的示例，说明了如何使用欧氏距离在电子商务中进行商品推荐。根据用户的历史购买行为，你可以计算他们之间的欧氏距离，并推荐那些与目标用户相似的其他用户已经购买的商品。这有助于提高销售和用户满意度。

（三）曼哈顿距离

曼哈顿距离（Manhattan Distance），也称为城市街区距离，是一种用于测量两个点在多维空间中的距离的距离度量方法。它得名于曼哈顿的街区布局，其中交叉点的距离通常是通过水平和垂直路线测量的。

假设有两个点 A 和 B，它们在二维空间中的坐标分别是 (x1, y1) 和 (x2, y2)。曼哈顿距离计算这两个点之间的距离，可以使用以下公式：

曼哈顿距离 = |x2 - x1| + |y2 - y1|

在这个例子中，我们有：

x1 = 2, y1 = 3（对应点 A 的坐标）

x2 = 4, y2 = 7（对应点 B 的坐标）

现在，我们可以将这些值代入公式计算曼哈顿距离：

曼哈顿距离 = |4 - 2| + |7 - 3|  = |2| + |4|  = 2 + 4  = 6

所以，点 A 和点 B 之间的曼哈顿距离是6。

与欧氏距离不同，曼哈顿距离是通过在每个维度上计算两个点坐标之间的差值的绝对值之和来度量的。这意味着曼哈顿距离在计算距离时只考虑了水平和垂直的移动，而不考虑对角线移动。

曼哈顿距离的主要特点包括：

• 直观性：曼哈顿距离类似于在城市中的行走距离，因此在实际生活中很容易理解。

• 非负性：曼哈顿距离永远是非负的。

• 各向异性：与欧氏距离不同，曼哈顿距离在各个维度上的权重是不一样的，它更适用于那些不同维度上的特征值具有不同重要性的情况。

曼哈顿距离在许多领域中有广泛的应用，包括路径规划、图像处理、特征选择、聚类分析等。它可以用于度量两个数据点之间的相似性或差异，根据具体情况来选择合适的距离度量方法。

（四）汉明距离

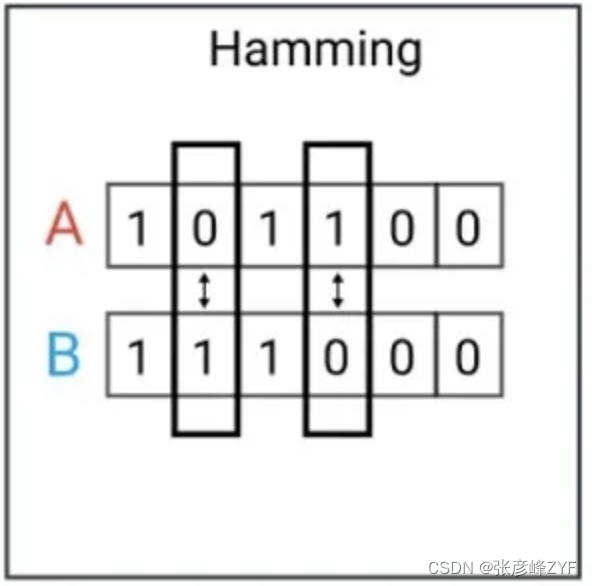
汉明距离（Hamming Distance）是一种用于比较两个等长字符串（通常是二进制字符串）之间的距离的度量方法。它衡量了两个字符串在相同位置上不同元素的数量。汉明距离的原理可以如下解释：

考虑两个等长的二进制字符串 A 和 B，每个字符串由 0 和 1 组成。汉明距离的计算方法是，将字符串 A 和字符串 B 逐位进行比较，统计它们在相同位置上不同元素的数量。如果 A 和 B 在某一位置上的元素不同，汉明距离增加1；如果它们在某一位置上的元素相同，汉明距离保持不变。

形式化地，汉明距离计算如下：

1. 假设字符串 A 和字符串 B 的长度都为 n。

2. 从第一个位置开始比较 A 和 B 的元素，如果它们不同，汉明距离增加1；如果它们相同，汉明距离不增加。

3. 继续比较下一个位置，重复步骤2，直到比较完所有的位置。

4. 汉明距离是累积的不同元素数量，即不同元素的个数。

这个度量方法得名于理论计算机科学家 Richard Hamming。汉明距离用于度量两个字符串或数据之间的差异，特别适用于处理错误检测和纠正编码、比特数据的相似性等问题。在通信、信息检索、图像处理和生物信息学等领域中经常使用汉明距离来度量数据的相似性或差异。

需要注意的是，汉明距离只适用于等长的字符串，而且只能用于度量二进制数据或离散数据的相似性。

三、基于集合的方法

Jaccard相似度和杰卡德距离是用于度量两个集合之间相似性和不相交性的度量方法。它们通常用于处理集合数据，例如文档的词汇集合、用户的兴趣集合和推荐系统中的物品集合。

（一）Jaccard相似度

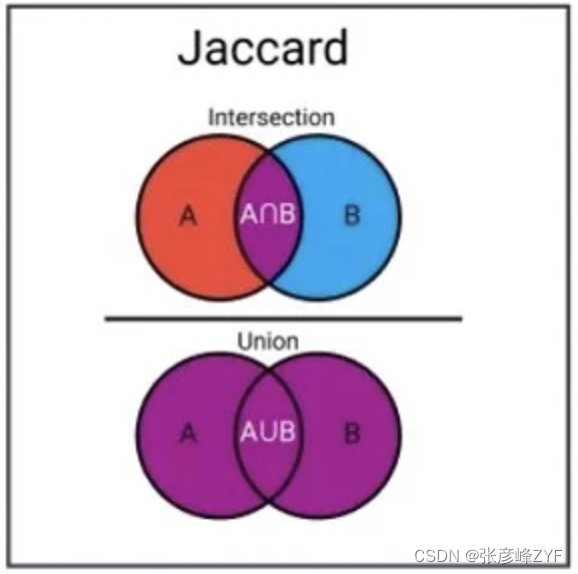
Jaccard相似度通常用于计算两个集合的交集与并集之间的比率。Jaccard相似度的计算公式如下：

Jaccard相似度 = (A ∩ B) / (A ∪ B)

其中，A 和 B 分别表示两个集合的元素，A ∩ B 表示它们的交集，A ∪ B 表示它们的并集

Jaccard相似度的值范围在0到1之间，0表示两个集合没有共同的元素，1表示两个集合完全相同。Jaccard相似度适用于度量集合的相似性，例如，在文档相似性计算中，可以使用文档中的词汇集合来计算它们之间的相似度。

应用举例：

• 文档相似性：在文本挖掘中，可以将文档表示为词汇集合，然后使用Jaccard相似度来比较文档之间的相似性。这对于文档检索、文档聚类和信息检索非常有用。
• 推荐系统：在推荐系统中，可以使用Jaccard相似度来衡量用户之间的兴趣相似性。根据用户的行为历史，可以推荐具有相似兴趣的物品给他们。
• 集合比较：在数据分析中，Jaccard相似度可用于比较两个数据集之间的相似性，例如，在市场篮子分析中，可以衡量不同消费者购买行为的相似性。

总之，Jaccard相似度允许我们比较不同集合的相似性，而不需要考虑元素的顺序，只关注元素的存在与否。

当使用Jaccard相似度来比较两个集合的相似性时，可以考虑以下案例：假设社交媒体公司想计算社交媒体平台上两位用户的兴趣相似性，以便为他们提供更好的朋友推荐。现在已经收集了两位用户的兴趣集合，这些集合包含各自关注的话题和兴趣。

用户 A 的兴趣集合：{"音乐", "电影", "体育", "旅游"}

用户 B 的兴趣集合：{"音乐", "美食", "体育", "科技"}

现在，可以使用Jaccard相似度来计算用户 A 和用户 B 的兴趣相似性。计算两位用户的兴趣集合的交集和并集。

交集（共同兴趣）：{"音乐", "体育"}

并集（总兴趣）：{"音乐", "电影", "体育", "旅游", "美食", "科技"}

使用Jaccard相似度的公式计算相似度：

Jaccard相似度 = (交集大小) / (并集大小) = 2 / 6 = 1/3 ≈ 0.33

所以，用户 A 和用户 B 的兴趣相似度约为0.33。

这个案例说明了如何使用Jaccard相似度来计算两位社交媒体用户的兴趣相似性。

（二）杰卡德距离

杰卡德距离是用于度量两个集合之间不相交性的度量方法，它是Jaccard相似度的互补度量。杰卡德距离的计算方式是计算两个集合的不相交部分占总部分的比率。杰卡德距离的计算公式如下：

杰卡德距离 = 1 - Jaccard相似度

与Jaccard相似度不同，杰卡德距离的值范围在0到1之间，0表示两个集合完全不相交，1表示两个集合完全相同。杰卡德距离越接近0，说明两个集合的不相交部分越大。

应用举例：

• 集合比较：杰卡德距离可用于比较两个数据集之间的不相交性。在数据分析和数据挖掘中，它可以用来识别不同集合之间的相似性或差异，例如，在市场篮子分析中，可以用来衡量不同消费者购买行为的差异。
• 数据清洗：杰卡德距离可以用于识别数据中的重复项或近似重复项。通过比较数据项之间的相异度，可以帮助识别可能的重复数据。
• 文本去重：在文本挖掘中，杰卡德距离可以用于识别文档集合中的重复文档或高度相似的文档，有助于文本去重和信息检索。

现在，可以使用杰卡德距离来比较用户 A 和用户 B 的兴趣集合的不相交性。

杰卡德距离 = 1 - Jaccard相似度 = 1 - 0.33 = 0.67

所以，用户 A 和用户 B 的兴趣相似性约为0.33，而杰卡德距离约为0.67。根据杰卡德距离的值，可以识别用户 A 和用户 B 之间的兴趣差异。杰卡德距离越接近0，表示他们的兴趣集合越相似；杰卡德距离越接近1，表示他们的兴趣集合越不相似。

四、基于内容的方法

五、协同过滤方法

（一）基于用户的协同过滤

基本理解总结

案列理解

（二）基于项目的协同过滤

基本理解总结

案列理解

六、基于图的方法

七、基于深度学习的方法

参考文章技术

「向量召回」相似检索算法——HNSW - 墨天轮

数据科学中常见的9种距离度量方法-大白智能