
然后我们来看一下梯度下降,这里先看一个叫
无约束最优化问题,,值得是从一个问题的所有可能的备选方案中选最优的方案,
我们的知道,我们的正态分布这里,正规的一个正态分布,还有我们的正规方程,他的这个x,是正规的,比如上面画的这个曲线,他的这个x,就是大于0的对吧,而现实生活中,
我们x的值可能是各种各样的没有约束的,基于没有约束的,这个问题..
我们来求导数,对y求导数得到,曲线的斜率,就叫做梯度下降
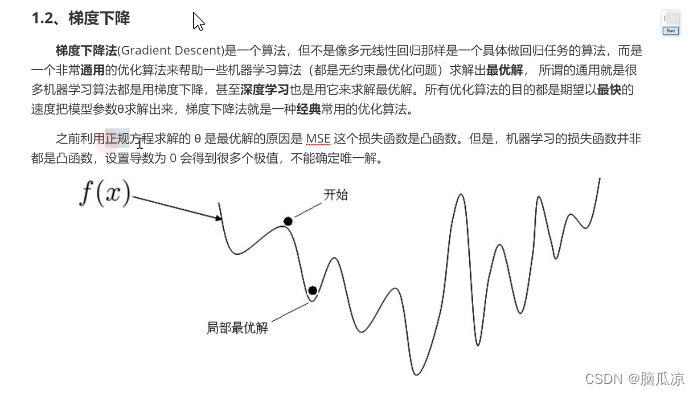
继续看,我们要找导数为0的,那么可以看到,底部
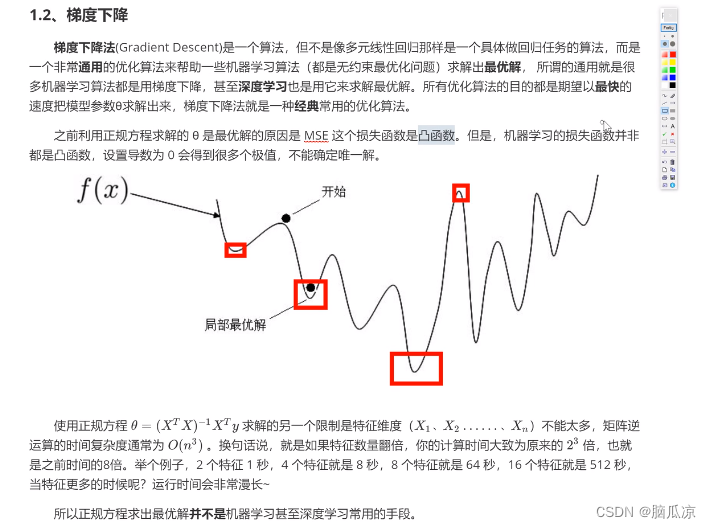
可以看到底部,和曲线的顶部都是斜率为0,导数为0对吧,但是
好在我们已经验证了,我们的最小二乘法,正态分布,对应的 是一个 开口向上的函数
所以我们找到的肯定是最低点对吧.

因为我们使用正规方程一次进行求解的话,花费的时间很长,可以看上面的说明.
所以我们只需要,令导数为0,然后这个就是斜率为0,求这个时候的seta是多少,其实就是模型w对吧
梯度下降法,其实就是,一点点去逼近这个最优解</





)





)
)

----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记)




)