取Dataset子集--pytorch
- 1. why
- 2. how
- 3. example
1. why
我们在调试深度学习代码时,常常会遇到数据集太大,导致调试浪费时间的情况,这种情况下,将数据集中的一个子集拿出来用于调试代码,调试成功在用完整的数据集运行代码成为一个可行的方案。
2. how
pytorch中Torch.utils.data.Subset()函数提供了一个简便的方式,函数如下,indices表示取子集中样本在dataset中的序号。
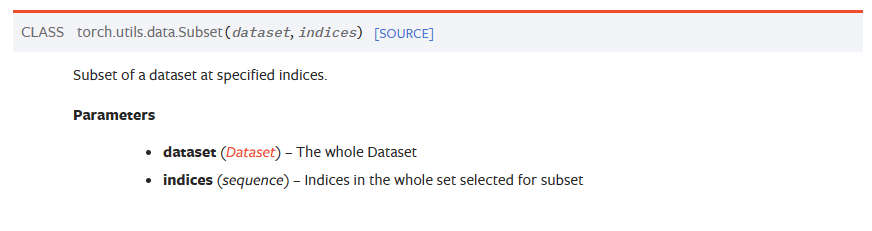
indices可以由以下的形式输入:
indices = range(0, 10) # or
indices = [x for x in range(10)]
3. example
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,download=True, transform=transform)
trainset = torch.utils.data.Subset(trainset,[0,1,2,3,4,5,6,7,8,9,10,11])
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,shuffle=True, num_workers=2)testset = torchvision.datasets.CIFAR10(root='./data', train=False,download=True, transform=transform)
testset = torch.utils.data.Subset(testset,[1,2,3,4])
testloader = torch.utils.data.DataLoader(testset, batch_size=4,shuffle=False, num_workers=2)


)





)
)









