【Hello Algorithm】滑动窗口内最大值最小值

滑动窗口介绍

滑动窗口是一种我们想象中的数据结构它是用来解决算法问题的

在这里插入图片描述

我们可以想象出一个数组然后再在这个数组的起始位置想象出两个指针 L 和 R

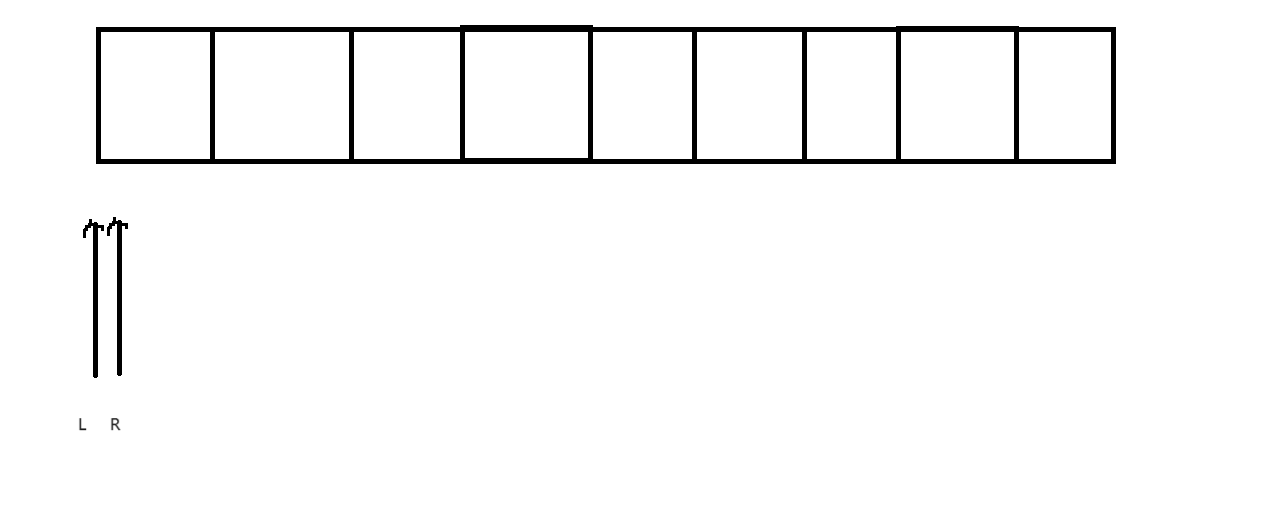
在这里插入图片描述

我们对于这两个指针做出以下规定

L 和 R指针只能往右移动
L指针不能走到R指针的右边
我们只能看到L指针和R指针中间的数字

比如说当前L和R指针重合我们就什么数字都看不见

如果此时R指针往右走一步那么我们就能看到L指针和R指针中间的数组的数字

又因为这种移动的方式特别像滑动所以说我们将这种想象出来的数据结构叫做滑动窗口

如何确定一个滑动窗口内的最大值

如果我们每次都遍历去获取滑动窗口的最大值的话那么每次获取的时间复杂度就是O（N）了这样子明显很复杂所以说我们需要想想别的方式去找到最大值

这里直接给出结论：

我们使用双端队列去获取一个滑动窗口内的最大值
双端队列的意义是：此时开始缩小滑动窗口哪些数字可能成为最大值

为了让双端队列能够实现它的意义我们做出以下规定

让R指针向右滑动的时候我们从右边插入数字的下标到双端队列中
如果说插入的数字要大于原来的数字我们让原来的数字出队列
让L指针向右滑动的时候我们从左边开始比较双端队列第一个（左边数起）下标和L指针的下标
如果说L指针的下标要大于双端队列最左边的下标则将其弹出

至于C++中的双端队列大家可以参考这篇博客双端队列

窗口内最大值

假设一个固定大小为W的窗口依次划过数组arr

让你依次返回每次窗口移动时窗口中的最大值

假设数组arr为【4 ， 3 ， 5 ，4， 3， 3， 6， 7】 W = 3

返回【5 ， 5， 5， 4， 6， 7】

这道题目实际上就是一个滑动窗口最大值的简单版本

我们使用一个双端队列就能很轻松的实现

面对这个问题我们可以拆分成两部分来解决

首先把滑动窗口的大小扩大到3
接着滑动窗口整体开始移动

两部分的代码都不算难代码表示如下

void process5(vector<int>& arr , vector<int>& ans , int W)
{deque<int> dq(0  , 0);for (int R = 0; R < W; R++){while (!dq.empty() && arr[dq.front()] <= arr[R]){dq.pop_back();}    dq.push_back(R);    }

  int R = W - 1;    int L = 0;    int N = static_cast<int>(arr.size());    while (R < N)    {    while (!dq.empty() && arr[dq.back()] <= arr[R])                                                                                                                          { dq.pop_back();}                     dq.push_back(R);while (L > dq.front())    {                         dq.pop_front();}                     ans.push_back(arr[dq.front()]);L++;    R++;}
}

这道题目给我们的提醒主要有两个

当我们R指针右移的时候要使用while来进行判断
R指针在初始化之后要重置否则会出现一些错误为了避免这些错误我们最好每次使用一个变量之前对其进行初始化

子数组中符合条件的个数

给定一个整形数组arr 和一个整数num

某个arr中的子数组sub 必须要满足

sub中的最大值减去sub中的最小值小于等于num

返回sub中达标的子数组的数量

我们首先分析下问题

如果我们没有学过滑动窗口和双端队列那么这道题我们会使用暴力的方式来得到答案

三个for循环嵌套时间复杂度就变成了n的三次方这显然是不可以的

当我们使用滑动窗口解决这个问题的时候由于我们的左右两个下标都是单向的往右边移动所以说此时的时间复杂度就是N

当我们得到两个下标满足上述条件时比如说0 ~ N上的最大值减去0~N中的最小值小于等于num

此时我们就可以说左下标为0 右下标为0 ~ N-1上的任意一个子数组都满足条件

因为此时最大值只有可能变小最小值只有可能变大所以说它们之间的差值肯定还是会小于等于num

所以我们就能确定以0为左边界 N为右边界上符合条件的子数组有 N - 0 + 1个

之后我们左边界右移即可

整体思路如下

我们使用两个双端队列来记录子数组的最大值和最小值
我们让右边界一直右移动直到子数组不满足条件为止
此时通过上面的技巧计算出左边界到右边界-1的满足条件子数组个数之后左边界++

代码表示如下

int process(vector<int>& arr, int num)
{deque<int> Max_Win(0, 0);deque<int> Min_Win(0, 0);int count = 0;int R = 0;int N = static_cast<int>(arr.size());for (int L = 0; L < N; L++){while (R < N){while (!Max_Win.empty() && arr[Max_Win.back()] <= arr[R]){Max_Win.pop_back();}Max_Win.push_back(R);while (!Min_Win.empty() && arr[Min_Win.back()] >= arr[R]){Min_Win.pop_back();}Min_Win.push_back(R);if (arr[Max_Win.front()] - arr[Min_Win.front()] > num){break;}else{R++;}}count += R - L;if (Max_Win.front() == L){Max_Win.pop_front();}if (Min_Win.front() == L){Min_Win.pop_front();}}return count;
}

这里有一点需要注意的是

 count += R - L;

语句必须要放到while循环的外面才行否则会因为R下标越界的问题而导致不会执行if语句最终导致count计算不完整

加油站的良好出发点问题

此时我们有两个数组 gas 和 cost

gas数组的意思每个加油点可以加多少单位的油

cost数组的意思是从当前加油点到下个加油点需要花费多少油（如果下个加油点不存在则视为是第一个加油点）

问题是假设从其中任意一个加油点触发起始车里没有油能否跑完一圈？

我们可以稍微理解下这个问题起始两个数组gas 和 cost 可以转化为一个 rest 数组

如果 rest 数组中有小于0的值则说明从该出发点无法跑通如果没有则说明可以跑通

其实我们想到了这一层就应该能联想到要使用窗口内最小值来解这道题目了但是这里又会出现一个新的问题 – 如果我们的起点不是从0下标开始的那么整个数组就需要 “拐弯”

对于这个问题的解决方式是我们可以将整个数组扩容到原来的双倍

根据原来的数组我们可以建立一个新的数组并且将每个数组位置的含义变为汽车到该加油站时剩余的单位油量超出原数组的部分我们从0下标开始再顺序循环一遍

这样子我们就可以使用滑动窗口来解决这个问题了解决步骤如下

设置原数组的大小为窗口大小
每次窗口移时选取一个最小值

代码表示如下

void process(vector<int>& arr , int num , vector<int>& ans)
{deque<int> Min_Win(0 , 0);for (int R = 0; R < num ; R++){while(!Min_Win.empty() && arr[Min_Win.back()] >= arr[R]){Min_Win.pop_back();}Min_Win.push_back(R);}                    int R = num - 1;   int L = 0;        while (R < static_cast<int>(arr.size()))  {  while(!Min_Win.empty() && arr[Min_Win.back()] >= arr[R])  {                         Min_Win.pop_back();  }                             Min_Win.push_back(R);                                     if (Min_Win.front() == L)  {  Min_Win.pop_front();  }                      L++;  R++;  if (arr[Min_Win.front()] < 0)  {                                       ans.push_back(0);  }  else                                                         {      ans.push_back(1);                                                                                                                                                                                                                                             }                                                                                                                                  }                                                                                                                                                                                                                                                                          
}