快速排序
分治
快速排序与归并排序的分治之间的不同:
归并排序的计算量主要消耗于有序子向量的归并操作,而子向量的划分却几乎不费时间;
快速排序恰好相反,它可以在O(1)时间内,由子问题的解直接得到原问题的解;但为了将原问题划分为两个子问题,却需要O(n)时间。
快速排序虽然能够确保划分出来的子任务彼此独立,并且其规模总和保持渐进不变,却不能保证两个子任务的规模大体相当(容易造成不平衡的情况)。
轴点
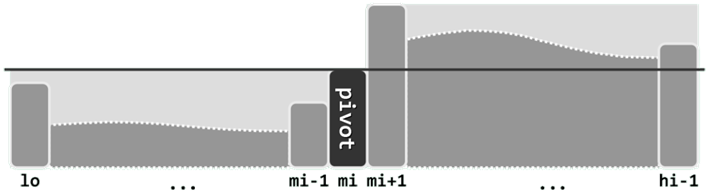
考查任一向量区间S[lo, hi)。对于任何lo <= mi < hi,以元素S[mi]为界,都可分割出前、后两个子向量S[lo, mi)和S(mi, hi)。若S[lo, mi)中的元素均不大于S[mi],且S(mi, hi)中的元素均不小于S[mi],则元素S[mi]称作向量S的一个轴点。
向量S经排序可转化为有序向量S',轴点位置mi必然满足:
a)S[mi] = S'[mi];
b)S[lo, mi) 和S'[lo, mi);
c)S(mi, hi) 和S'(mi, hi);
采用分治策略,递归地利用轴点的以上特性,便可完成原向量的整体排序。
快速排序算法
轴点的位置一旦确定,则只需以轴点为界,分别递归地对前、后子向量实施快速排序;子向量的排序结果就地返回之后,原向量的整体排序即告完成。
template <typename T> //向量快速排序
void vector<T>::quickSort ( Rank lo,Rank hi ) { //0 <= lo < hi <= sizeif ( hi - lo < 2 ) return; //单元素区间自然有序,否则...Rank mi = partition ( lo, hi - 1 ); //在[lo, hi - 1]内构造轴点quickSort ( lo,mi ); //对前缀递归排序quickSort ( mi + 1, hi ); //对后缀递归排序
}
算法的核心与关键在于 :轴点构造算法partition() 的实现
快速划分算法

任一元素作为轴点的必要条件之一是,其在初始向量S与排序后有序向量S'中的秩应当相同。
只要向量中所有元素都是错位的,即所谓的错排序列。则任何元素都不可能是轴点。若保持原向量的次序不变,则不能保证总是能够找到轴点。
为在区间[lo, hi]内构造出一个轴点,首先需要任取某一元素m作为“培养对象”。

如图(a)所示,不妨取首元素 m = S[lo] 作为候选,将其从向量中取出并做备份,腾出的空闲单元便于其它元素的位置调整。然后如图(b)所示,不断试图移动lo和hi,使之相互靠拢。当然,整个移动过程中,需始终保证lo(hi)左侧(右侧)的元素均不大于(不小于)m。
最后如图( c)所示,当lo与hi彼此重合时,只需将原备份的m回填至这一位置,则S[lo = hi]= m便成为一个名副其实的轴点。
以上过程在构造出轴点的同时,也按照相对于轴点的大小关系,将原向量划分为左、右两个子向量,故亦称作快速划分算法。
template <typename T> //轴点构造算法∶通过调整元素位置构造区间[lo,hi]的轴点,并返回其秩
Rank Vector<T>::partition ( Rank lo,Rank hi ) { //版本A︰基本形式swap ( _elem[lo], _elem[lo + rand() % ( hi - lo + 1 ) ] ); //任选一个元素与首元素交换T pivot = _elem[lo]; //以首元素为候选轴点——经以上交换,等效于随机选取while ( lo < hi ) { //从向量的两端交替地向中间扫描while ( ( lo < hi ) && ( pivot <= _elem[hi] ) ) //在不小于pivot的前提下hi--; //向左拓展右端子向量_elem[lo] = _elem[hi]; //小于pivot者归入左侧子序列while ( ( lo < hi ) && ( _elem[lo] <= pivot ) ) //在不大于pivot的前提下lo++; //向右拓展左端子向量_elem[hi] = _elem[lo]; //大于pivot者归入右侧子序列} //assert: lo == hi_elem[ lo] = pivot; //将备份的轴点记录置于前、后子向量之间return lo; //返回轴点的秩
}
过程
算法的主体框架为循环迭代;主循环的内部,通过两轮迭代交替地移动lo和hi。

如图(a)所示。反复地将候选轴点pivot与当前的_elem[hi]做比较,只要前者不大于后者,就不断向左移动hi(除非hi即将越过lo);
hi无法移动继续时,当如图(b)所示。
接下来如图( c )所示,将 _elem[hi] 转移至 _elem[lo],并归入左侧子向量。
随后对称地,将_elem[lo]与pivot做比较,只要前者不大于后者,就不断向右移动lo(除非lo即将越过hi)
lo无法继续移动时,当如图(d)所示。
接下来如图(e)所示,将_elem[lo]转移至_elem[hi],并归入右侧子向量。
如此实现的快速排序算法并不稳定。
该算法的运行时间线性正比于被移动元素的数目,线性正比于原向量的规模O(hi - lo)
复杂度
最坏情况: 若每次都是简单地选择最左端元素_elem[lo]作为候选轴点,则对于完全(或几乎完全)有序的输入向量,每次(或几乎每次)划分的结果都是如此:T(n) = T(n - 2) + 2∙O(n) = ... = T(0) + n∙O(n) = O(n^2 )
效率低到与起泡排序相近。
平均运行时间
在大多数情况下,快速排序算法的平均效率依然可以达到O(nlogn);而且较之其它排序算法,其时间复杂度中的常系数更小。
改进
partition()算法的版本A对此类输入的处理完全等效于此前所举的最坏情况。
事实上对于此类向量,主循环内部前一子循环的条件中“pivot <= _elem[hi]”形同虚设,故该子循环将持续执行,直至“lo < hi”不再满足。当然,在此之后另一内循环及主循环也将随即结束。
可以在每次深入递归之前做统一核验,若确属退化情况,则无需继续递归而直接返回。但在重复元素不多时,如此不仅不能改进性能,反而会增加额外的计算量,总体权衡后得不偿失。
template <typename T> //轴点构造算法︰通过调整元素位置构造区间[lo,hi]的轴点,并返回其秩
Rank Vector<T>: : partition ( Rank lo,Rank hi ) { //版本B∶可优化处理多个关键码雷同的退化情况swap ( _elem[lo],_elem[lo + rand() % ( hi - lo + 1 ) 〕);//任选一个元素与首元素交换T pivot = _elem[lo]; //以首元素为候选轴点——经以上交换,等效于随机选取while ( lo < hi ) { //从向量的两端交替地向中间扫描while ( lo < hi )if ( pivot < _elem[hi] ) //在大于pivot的前提下hi--; //向左拓展右端子向量else //直至遇到不大于pivot者{ _elem[lo++] =_elem[hi]; break; }//将其归入左端子向量while ( lo < hi )if ( _elem[ lo] < pivot ) //在小于pivot的前提下lo++; //向右拓展左端子向量else //直至遇到不小于pivot者{ _elem[hi--] = _elem[ lo]; break; } //将其归入右端子向量} // assert: lo == hi_elem[lo] = pivot; //将备份的轴点记录置于前、后子向量之间return lo; //返回轴点的秩
}
一旦遇到重复元素,右端子向量随即终止拓展,并将右端重复元素转移至左端。
较之版本A,版本B主要是调整了两个内循环的终止条件。以前一内循环为例,原条件:pivot <= _elem[hi] 改为了:pivot < _elem[hi]。
性能
对于由重复元素构成的输入向量,版本B将交替地将右(左)侧元素转移至左(右)侧,并最终恰好将轴点置于正中央的位置。
意味着,退化的输入向量能够始终被均衡的切分,如此反而转为最好情况,排序所需时间为O(nlogn)。
选取与中位数
从与这组元素对应的有序序列S中,找出秩为k的元素S[k],故称作选取问题。若将目标元素的秩记作k,则亦称作k-选取。

中位数:在长度为n的有序序列S中,位序居中的元素 S[n/2] 向上取整称作中值或中位数。
即便对于尚未排序的序列,也可定义中位数——也就是在对原数据集排序之后,对应的有序序列的中位数。
蛮力算法
对所有元素做排序,将其转换为有序序列S;于是,S[n/2]便是所要找的中位数。
最坏情况下需要O(nlogn)时间。
因此,基于该算法的任何分治算法,时间复杂度都会不低于:T(n) = nlogn + 2∙T(n/2) = O(n log^2 n)。
如何在避免全排序的前提下,在 o(nlogn) 时间内找出中位数?
众数
在任一无序向量A中,若有一半以上元素的数值同为m,则将m称作A的众数。
若众数存在,则必然同时也是中位数。
否则,在对应的有序向量中,总数超过半数的众数必然被中位数分隔为非空的两组——与向量的有序性相悖。
template <typename T> bool majority ( Vector<T> A, T& maj ) { //众数查找算法∶T可比较可判等maj = majEleCandidate ( A ); //必要性:选出候选者majreturn majEleCheck ( A, maj ); //充分性:验证maj是否的确当选
}
设 P 为向量A 中长度为 2m 的 前缀。若元素x 在P 中恰好出现m 次,则A有众数仅当后缀 A-P拥有众数,且 A-P 的众数就是A 的众数。

实现: 自左向右地扫描一遍整个向量,即可唯一确定满足如上必要条件的某个候选者。
若A的众数就是x,则在剪除前缀P之后,x与非众数均减少相同的数目,二者数目的差距在后缀A-P中保持不变。
反过来,若A的众数为 y!= x,则在剪除前缀P之后,y减少的数目也不致多于非众数减少的数目,二者数目的差距在后缀A-P中也不会缩小。
template <typename T> T majElecandidate ( Vector<T>A ) {//选出具备必要条件的众数候选者T maj;//众数候选者
//线性扫描:借助计数器c,记录maj与其它元素的数量差额for ( int c = 0, i = 0; i < A.size(); i++ )if ( 0 == c ) { //每当c归零,都意味着此时的前缀P可以剪除maj = A[i]; c = 1; //众数候选者改为新的当前元素}else //否则maj == A[i] ? c++ : c--; //相应地更新差额计数器return maj; //至此,原向量的众数若存在,则只能是maj——尽管反之不然
}
其中,变量 maj 始终为当前前缀中出现次数不少于一半的某个元素;c则始终记录该元素与其它元素的数目之差。
一旦c归零,则意味着如图(b)所示,在当前向量中找到了一个可剪除的前缀P。在剪除该前缀之后,问题范围将相应地缩小至A-P。此后,只需将maj重新初始化为后缀A-P的首元素,并令c = 1,即可继续重复上述迭代过程。
归并向量的中位数
任给有序向量 S 1 S_1 S1 和 S 2 S_2 S2 ,如何找出它们归并后所得有序向量 S = S 1 ∪ S 2 S = S_1 \cup S_2 S=S1∪S2 的中位数?
蛮力算法
//中位数算法蛮力版∶效率低,仅适用于max(n1, n2)较小的情况
template <typename T> //子向量s1[lo1,lo1 + n1)和s2[1o2,lo2 + n2)分别有序,数据项可能重复
T trivialMedian ( Vector<T>& S1,int lo1, int n1,Vector<T>& S2,int lo2,int n2 ) {int hi1 = lo1 + n1, hi2 = lo2 + n2;Vector<T> S; //将两个有序子向量归并为一个有序向量while ( ( lo1 < hi1 ) &&( lo2 < hi2 ) ) {while ( ( lo1 < hi1 ) && s1[lo1] <= S2[lo2] ) S.insert( S1[lo1 ++] );while ( ( lo2 < hi2 ) && S2[lo2] <= S1[1o1] ) S.insert( S2[lo2 ++] );}while ( lo1 < hi1 ) s.insert ( s1[lo1 ++] );while ( lo2 < hi2 ) s.insert ( s1[lo2 ++] );return S[ ( n1 + n2 ) / 2]; //直接返回归并向量的中位数
}
诚然,有序向量S中的元素 S[(n 1 + n 2 )/2] 即为中位数,但若按代码中蛮力算法 trivialMedian() 将二者归并,则需花费 O ( n 1 + n 2 ) O(n_1 + n_2) O(n1+n2) 时间。这一效率虽不算太低,但未能充分利用“两个子向量已经有序”的条件。
减而治之
考查 S 1 S_1 S1 的中位数 m 1 = S 1 [ n / 2 ] m_1 = S_1 [n/2] m1=S1[n/2] 和 S 2 S_2 S2 的逆向中位数 m 2 = S 2 [ n / 2 − 1 ] = S 2 [ ( n − 1 ) / 2 ] m_2 = S_2 [n/2 - 1] = S_2 [(n - 1)/2] m2=S2[n/2−1]=S2[(n−1)/2],并比较其大小。
n为偶数和奇数的情况,分别如图(a)和图(b)所示。

若 m 1 = m 2 m_1 = m_2 m1=m2 ,则在 S = S 1 ∪ S 2 S = S_1\cup S_2 S=S1∪S2 中,各有 n / 2 + (n / 2 - 1) = n - 1个元素不大于和不小于它们,故 m1 和 m2 就是 S 的中位数;
若 m 1 < m 2 m_1 < m_2 m1<m2 ,则意味着在S中各有n/2个元素(图中以灰色示意)不大于和不小于它们。可见,这些元素或者不是S的中位数,或者与 m1 或 m2 同为S的中位数。
综合以上分析,只需进行一次比较,即可将原问题的规模缩减大致一半。
整个算法呈线性递归的形式,递归深度不超过 log2 n,每一递归实例仅需常数时间,故总体时间复杂度仅为O(logn)——这一效率远远高于蛮力算法。
template <typename T> //序列s1[lo1,lo1 + n)和S2[1lo2,lo2 + n)分别有序,n > 0,数据项可能重复
T median ( Vector<T>& s1, int lo1,Vector<T>& s2, int lo2, int n ) { //中位数算法(高效版)if ( n < 3 ) return trivialMedian ( s1, lo1, n, s2, lo2, n );//递归基int mi1 = lo1 + n / 2, mi2 = lo2+ ( n - 1 ) / 2;//长度(接近)减半if ( s1[mi1] < s2[mi2] )return median ( s1, mi1, s2, lo2, n + lo1 - mi1 );//取s1右半、s2左半else if ( s1[mi1] > s2[mi2] )return median ( s1, lo1,s2, mi2, n + lo2 - mi2 );//取s1左半、s2右半elsereturn s1[mi1];
基于优先级队列的选取
蛮力算法效率低的原因:一组元素中第k大的元所包含的信息量,远远少于经过全排序后得到的整个有序序列。花费足以全排序的计算成本,却仅得到了少量的局部信息。
只需获取原数据集的局部信息——优先级队列结构
基于堆结构的选取算法大致有三种。
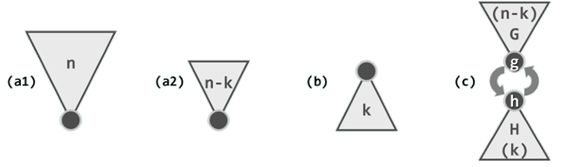
第一种算法如图(a1)所示。首先,花费O(n)时间将全体元素组织为一个小顶堆;然后,经过k次delMin()操作,则如图(a2)所示得到位序为k的元素。
算法的运行时间为:O(n) + k∙O(logn) = O(n + klogn)
第二种算法如图(b)所示。任取k个元素,并在O(k)时间以内将其组织为大顶堆。然后将剩余的n - k个元素逐个插入堆中;每插入一个,随即删除堆顶,以使堆的规模恢复为k。待所有元素处理完毕之后,堆顶即为目标元素。
算法的运行时间为:O(k) + 2(n - k)∙O(log k) = O(k + 2(n - k)log k)
第三种算法如图(c )所示。首先将全体元素分为两组,分别构建一个规模为n - k的小顶堆G和一个规模为k的大顶堆H。接下来,反复比较它们的堆顶g和h,只要g < h,则将二者交换,并重新调整两个堆。如此,G的堆顶g将持续增大,H的堆顶h将持续减小。当g >= h时,h即为所要找的元素。
算法的运行时间为:O(n - k) + O(k) + min(k, n - k)∙2∙(O(log k + log(n - k)))
在目标元素的秩很小或很大(即|n/2 - k| ≈ n/2)时,上述算法的性能都还不错。
k ≈ 0 时,前两种算法均只需O(n)时间。然而,当 k ≈ n/2 时,以上算法的复杂度均退化至蛮力算法的O(nlogn)。
基于快速划分的选取
逐步逼近
首先,调用算法partition()构造向量A的一个轴点A[i] = x。若i =k,则该轴点恰好就是待选取的目标元素,即可直接将其返回。
反之,若如图所示 i != k。

如图(a),k < i,则选取的目标元素不可能(仅)来自于处于x右侧、不小于x的子向量(白色)G中。此时,不妨将子向量G剪除,然后递归地在剩余区间继续做k-选取。
如图(b),i < k,则选取的目标元素不可能(仅)来自于处于x左侧、不大于x的子向量(白色)L中。同理,此时也可将子向量L剪除,然后递归地在剩余区间继续做 (k - i)-选取。
实现
template <typename T> void quickSelect ( Vector<T>& A,Rank k ) { //基于快速划分的k选取算法for ( Rank lo = 0, hi = A.size() - 1; lo < hi; ) {Rank i = lo, j = hi; T pivot = A[lo];while ( i <j ) { //o(hi - lo + 1) = o(n)while ( ( i<j ) && ( pivot <= A[j] ) ) j--; A[i] = A[j];while ( ( i <j ) &&( A[i]<= pivot ) ) i++; A[j] = A[i];} //assert: i == jA[i] = pivot;if ( k <= i ) hi = i - 1;if ( i <= k ) lo = i + 1;} //A[k] is now a pivot
}
每经过一步主迭代,都会构造出一个轴点A[i],然后lo和hi将彼此靠拢,查找范围将收缩至A[i]的某一侧。当轴点的秩i恰为k时,算法随即终止。如此,A[k]即是待查找的目标元素。
尽管内循环仅需O(hi - lo + 1)时间,但外循环的次数却无法有效控制。与快速排序算法一样,最坏情况下外循环需执行O(n)次,总体运行时间为O(n^2)
K-选取算法

将该select()算法在最坏情况下的运行时间记作T(n),其中n为输入序列A的规模。
显然,第1)步只需O(n)时间。既然Q为常数,故在第2)步中,每一子序列的排序及中位数的计算只需常数时间,累计不过O(n)。第3)步为递归调用,因子序列长度为n/Q,故经过T(n/Q)时间即可得到全局的中位数M。第4)步依据M对所有元素做分类,为此只需做一趟线性遍历,累计亦不过O(n)时间。
算法的第5)步尽管会发生递归,但需进一步处理的序列的规模,绝不致超过原序列的3/4。
综上,可得递推关系如下:T(n) = cn + T(n/Q) + T(3n/4),c为常数
希尔排序
递减增量策略
希尔排序(Shellsort) 算法首先将整个待排序向量A[]等效地视作一个二维矩阵B[][]。
若原一维向量为A[0, n),则对于任一固定的矩阵宽度w,A与B中元素之间总有一一对应关系:B[i][j] = A[iw + j] 或 A[k] = B[k / w][k % w]。

从秩的角度来看,矩阵B的各列依次对应于整数子集[0, n)关于宽度w的某一同余类。这也等效于从上到下、自左而右地将原向量A中的元素,依次填入矩阵B的各个单元。
假设w整除n。如此,B中同属一列的元素自上而下依次对应于A中以w为间隔的n/w个元素。因此,矩阵的宽度w亦称作增量。
希尔排序的算法框架:

希尔排序是个迭代式重复的过程,每一步迭代中,都从事先设定的某个整数序列中取出一项,并以该项为宽度,将输入向量重排为对应宽度的二维矩阵,然后逐列分别排序。

因为增量序列中的各项是逆向取出的,所以各步迭代中矩阵的宽度呈缩减的趋势,直至最终使用w1 = 1。
矩阵每缩减一次并逐列排序一轮,向量整体的有序性就得以进一步改善。当增量缩减至1时,矩阵退化为单独的一列,故最后一步迭代中的“逐列排序”等效于对整个向量执行一次排序。
通过不断缩减矩阵宽度而逐渐逼近最终输出的策略,称作递减增量算法,这也是希尔排序的另一名称。
#include <iostream>
#include <vector>void shellSort(std::vector<int>& arr) {int n = arr.size();// 初始化间隔hfor (int h = n / 2; h > 0; h /= 2) {// 对各个子序列进行插入排序for (int i = h; i < n; i++) {int temp = arr[i];int j;for (j = i; j >= h && arr[j - h] > temp; j -= h) {arr[j] = arr[j - h];}arr[j] = temp;}}
}int main() {std::vector<int> data = {12, 34, 11, 3, 56, 87, 45, 24, 91, 75};std::cout << "原始数组: ";for (int val : data) {std::cout << val << " ";}std::cout << std::endl;shellSort(data);std::cout << "希尔排序后的数组: ";for (int val : data) {std::cout << val << " ";}std::cout << std::endl;return 0;
}
希尔排序的核心思想是通过比较和交换不相邻的元素,以最大步长对元素进行分组。然后逐步减小步长,最终完成排序。
具体过程如下:
步长(间隔)选择: 选择一个初始的步长(间隔)h。通常,初始步长可以是数组长度的一半,并逐步减小步长直至为1。
间隔排序: 将整个数组分割成若干个子序列,分别对每个子序列进行插入排序。在每个子序列中,对应间隔为h的元素进行排序。
逐步减小间隔: 不断减小步长h,重复上述过程。这个过程会继续进行直到步长h等于1。
希尔排序的时间复杂度取决于步长序列的选择。它的平均时间复杂度为O(n log n)到O(n^2)之间。


(SpringBoot))
)













)

-创建型模式)