网络流基础
基本概念
-
源点(source) s s s,汇点 t t t。
-
容量:约等于边权。不存在的边流量可视为 0 0 0。 ( u , v ) (u,v) (u,v) 的流量通常记为 c ( u , v ) c(u,v) c(u,v)(capacity)。
-
流(flow):每条边上的流不能超过它的容量,注意这个限制是所有经过路径的边共享的。除了源点和汇点,其他所有点流入的流量都等于流出的流量。通常用 f f f 表示。
-
割:把结点分成两部分 { S , T } \{S,T\} {S,T},且满足 s ∈ S , t ∈ T s\in S,t\in T s∈S,t∈T, { S , T } \{S,T\} {S,T} 是图的一个 s s s- t t t 割, s s s- t t t 割 { S , T } \{S,T\} {S,T} 的容量为 ∑ u ∈ S ∑ v ∈ T c ( u , v ) \sum\limits_{u\in S}\sum\limits_{v\in T}c(u,v) u∈S∑v∈T∑c(u,v)。
-
残留网络:有源点、汇点,且每条边都有残留容量的网络。
-
增广路:从残留网络的源点到汇点的路径。对于增广路,给每一条边都加上等量流量,此过程称为增广。
常见问题
- 最大流问题:给定每条边的流量,求得尽可能大的流量。
- 最小割问题:给定每条边的流量,求一个容量尽可能大的 s s s- t t t 割 { S , T } \{S,T\} {S,T}。
- 最小费用最大流问题:给定每条边的流量和权值(费用),求对于所有可能的最大流,费用最小的一个。
- 上下界网络流问题:给定每条边的流量上界和下界,求一种可行的流使得满足限制。
最大流问题
以下代码均为 P3376 【模板】网络最大流 代码。
先介绍一种思想——Ford–Fulkerson 增广(FF 增广)。即不断在残留网络中找一条增广路,向汇点发送可能的最大流量,得到新的残留网络,不断寻找增广路,直到没有增广路为止。此时有最大流。
在 FF 增广的过程中,为了保证正确性,我们要引入反向边。对于每一条边 ( u , v ) (u,v) (u,v),建一条 c ( v , u ) = 0 c(v,u)=0 c(v,u)=0 的反向边。反向边其实相当于一种撤回操作,因此在增广的过程中,给正向边减去流量的同时要给反向边加上流量。
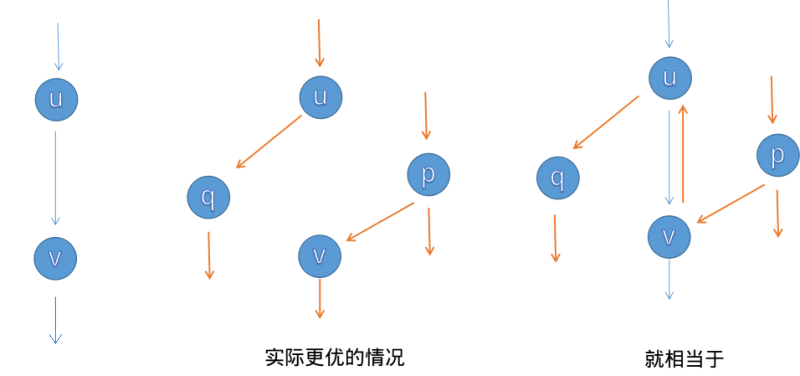
反向边的“抵消”操作使得在错误的增广路选择顺序下也可以得到正确答案。
FF 增广的时间复杂度为 O ( E f max ) O(Ef_{\max}) O(Efmax)。
EK 算法
通过 BFS 实现的 FF 增广过程。最坏时间复杂度为 O ( V E 2 ) O(VE^2) O(VE2),一般可以处理 1 0 4 10^4 104 规模的网络。
注意这里的链前 cnt 初始值要设定为 1 1 1,方便通过异或操作查找反向边(这样可以使第一条边的编号为偶数, 2 n ⊕ 1 = 2 n + 1 , ( 2 n + 1 ) ⊕ 1 = 2 n 2n \oplus 1=2n+1,(2n+1)\oplus 1=2n 2n⊕1=2n+1,(2n+1)⊕1=2n)。用 pre 数组记录当前的增广路,flow 数组记录当前增广路上的流量。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;const ll maxn=5005;
int n,m,s,t,cnt=1,head[maxn],pre[maxn];
ll flow[maxn]/*记录到x的最大可行流*/,ans;
struct edge{int to,nxt;ll c;}e[maxn*2];
bool vis[maxn],flag[205][205];void add(int x,int y,ll z){e[++cnt]={y,head[x],z},head[x]=cnt;}bool bfs()
{for(int i=1;i<=n;i++) vis[i]=0;queue<int> q;vis[s]=1,q.push(s),flow[s]=LLONG_MAX;while(!q.empty()){int x=q.front();q.pop();for(int i=head[x];i;i=e[i].nxt){if(!e[i].c) continue;if(vis[e[i].to]) continue;flow[e[i].to]=min(flow[x],e[i].c),pre[e[i].to]=i,q.push(e[i].to),vis[e[i].to]=1;if(e[i].to==t) return 1;}}return 0;
}void ek()
{int x=t;while(x!=s) e[pre[x]].c-=flow[t],e[pre[x]^1].c+=flow[t],x=e[pre[x]^1].to;ans+=flow[t];
}int main()
{cin>>n>>m>>s>>t;for(int i=1,u,v,w;i<=m;i++) cin>>u>>v>>w,add(u,v,w),add(v,u,0);while(bfs()) ek();cout<<ans;return 0;
}
Dinic 算法
先通过 BFS,把图根据结点到源点的距离分层,只按照层数递增的方向增广。注意每次增广后都要重新将图分层。
为了保证 Dinic 算法的时间复杂度正确性,我们需要引入当前弧优化。如果一条边 ( u , v ) (u,v) (u,v) 的容量已经用完,或 v v v 的后侧已经增广至阻塞,则 u u u 的流量无需流向出边 ( u , v ) (u,v) (u,v)。对于每个结点,维护它的出边中第一个需要尝试流出的出边。维护的这个指针称为当前弧。由于我们的边是顺次遍历的,所以当遍历到第 i i i 条边时,前面的边一定已经不能继续流,直接修改新的当前弧 now[x]=i。
还可以用多路增广的方法优化时间复杂度。在某点找到一条增广路后,如果还有剩余流量,继续从该点寻找增广路。
DFS 过程中,对于当前结点 x x x,它可以分给后面结点最多 f max f_{\max} fmax 流量;对于当前访问的边 ( u , v ) (u,v) (u,v),分配的流量是最大流量与已经用的流量之差与边的容量取 min \min min 的结果。
最坏时间复杂度为 O ( V 2 E ) O(V^2E) O(V2E)。
#include <bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;const int maxn=5005;
int n,m,s,t,cnt=1,head[maxn],now[maxn];
ll flow[maxn],ans,dis[205];
struct edge{int to,nxt;ll c;}e[maxn*2];void add(int x,int y,ll z){e[++cnt]={y,head[x],z},head[x]=cnt;}bool bfs()
{for(int i=1;i<=n;i++) dis[i]=LLONG_MAX;queue<int> q;q.push(s);dis[s]=0,now[s]=head[s];while(!q.empty()){int x=q.front();q.pop();for(int i=head[x];i;i=e[i].nxt)if(e[i].c>0&&dis[e[i].to]==LLONG_MAX){q.push(e[i].to),now[e[i].to]=head[e[i].to],dis[e[i].to]=dis[x]+1;if(e[i].to==t) return 1;}}return 0;
}int dfs(int x,ll mxf)//mxf是能给后面点分配的最大流量
{if(x==t) return mxf;ll sum=0;//sum是从x点实际分配出的流量for(int i=now[x];i;i=e[i].nxt){now[x]=i;if(e[i].c>0&&dis[e[i].to]==dis[x]+1){int ff=dfs(e[i].to,min(mxf-sum,e[i].c));e[i].c-=ff,e[i^1].c+=ff,sum+=ff;if(ff==mxf) return ff;}}return sum;
}signed main()
{cin>>n>>m>>s>>t;for(int i=1,u,v,w;i<=m;i++) cin>>u>>v>>w,add(u,v,w),add(v,u,0);while(bfs()) ans+=dfs(s,LLONG_MAX);cout<<ans;return 0;
}
最小费用最大流问题
当 ( u , v ) (u,v) (u,v) 流量为 f ( u , v ) f(u,v) f(u,v) 时,花费的费用为 f ( u , v ) × w ( u , v ) f(u,v)\times w(u,v) f(u,v)×w(u,v),要求在最大化 ∑ ( u , v ) ∈ E f ( u , v ) \sum\limits_{(u,v)\in E}f(u,v) (u,v)∈E∑f(u,v) 的情况下最小化 ∑ ( u , v ) ∈ E f ( u , v ) × w ( u , v ) \sum\limits_{(u,v)\in E} f(u,v)\times w(u,v) (u,v)∈E∑f(u,v)×w(u,v),该问题即最小费用最大流问题。
SSP 算法
SSP(Successive Shortest Path)算法,思想是每次寻找费用最小的增广路进行增广,直到图上不存在增广路为止。
注意图中不能存在单位费用为负的圈。
具体实现就是把 EK/Dinic 算法中 BFS 找增广路的过程用 SPFA 代替,同时反向边的花费为负。时间复杂度 O ( V E f max ) O(VEf_{\max}) O(VEfmax)。
以下是基于 EK 算法的实现:
#include <bits/stdc++.h>
using namespace std;const int maxn=5005,maxm=1e5+5;
struct edge{int to,nxt,c,w;}e[maxm];
int head[maxn],pre[maxn],dis[maxn],cnt=1,n,m,s,t,mxf,minc,flow[maxn];
bool vis[maxn];void add(int x,int y,int z,int q){e[++cnt]=(edge){y,head[x],z,q},head[x]=cnt;}bool spfa()
{queue<int> q;for(int i=1;i<=n;i++) dis[i]=INT_MAX,vis[i]=0;q.push(s),dis[s]=0,flow[s]=INT_MAX,vis[s]=1,pre[t]=-1;while(!q.empty()){int x=q.front();q.pop(),vis[x]=0;for(int i=head[x];i;i=e[i].nxt)if(e[i].c&&dis[e[i].to]>dis[x]+e[i].w){dis[e[i].to]=dis[x]+e[i].w,pre[e[i].to]=i,flow[e[i].to]=min(flow[x],e[i].c);if(!vis[e[i].to]) q.push(e[i].to),vis[e[i].to]=1;}}return pre[t]!=-1;
}void ek()
{while(spfa()){int x=t;mxf+=flow[t],minc+=flow[t]*dis[t];while(x!=s) e[pre[x]].c-=flow[t],e[pre[x]^1].c+=flow[t],x=e[pre[x]^1].to;// cout<<flow[t]<<' '<<dis[t]<<endl;}
}int main()
{cin>>n>>m>>s>>t;for(int i=1,u,v,w,c;i<=m;i++) cin>>u>>v>>w>>c,add(u,v,w,c),add(v,u,0,-c);ek();cout<<mxf<<' '<<minc;return 0;
}
程序连接报错问题)





【学习笔记(四)】)







)



![P1022 [NOIP2000 普及组] 计算器的改良 题解](http://pic.xiahunao.cn/P1022 [NOIP2000 普及组] 计算器的改良 题解)
)