C语言数据结构之数据结构入门

数据结构介绍

数据结构发展史

何为算法

数据结构基础

基本概念和术语

四大逻辑结构（Logic Structure）

数据类型

理解复杂度概念

时间空间复杂度定义

度量时间复杂度的方法

程序运行时的内存与地址

编程预备

数据结构介绍

数据结构发展史

起源：1968年美国唐•欧•克努特教授开创了数据结构的最初体系，他所著的《计算机程序设计技巧》第一卷《基本算法》是第一本较系统地阐述数据的逻辑结构和存储结构语其操作的著作。我们一般认为本书开创了数据结构的系统概念。70年代初，数据结构作为一门独立的课程开始进入大学课堂。

数据结构的发展经历三个阶段：无结构阶段，结构化阶段和面向对象阶段（和程序发展的三个阶段不谋而合了）

无结构阶段：在计算机发展的早期阶段，主要应用于科学计算。此时，程序设计主要使用机器语言和汇编语言，数据的表示和操作主要依赖数学公式和模型。数据结构的概念尚未形成，程序设计更注重数值计算而非数据之间的关系。
结构化阶段：随着计算机应用领域的扩大，人们开始关注程序设计规范化的重要性。在这个阶段，数据结构的概念逐渐形成，并引入了抽象数据类型（ADT）的概念。ADT将数据的表示和操作封装在一起，使得程序设计更加模块化和灵活。同时，各种基本的数据结构如数组、链表、栈、队列等得到广泛应用。此时，数据结构的教学和研究也开始兴起。
面向对象阶段：80年代初期至今，面向对象的程序设计方法逐渐流行起来。面向对象的设计思想将数据和操作封装在对象中，通过类和继承的机制实现数据结构的抽象和重用。这一阶段，数据结构变得更加丰富多样，大量的封装类如链表、树、图等被设计出来，使得程序设计者能够更方便地使用和操作数据结构。同时，面向对象的设计方法也提供了更好的模块化和可扩展性。

总的来说，数据结构的发展经历了无结构阶段、结构化阶段和面向对象阶段。随着计算机应用领域的扩大和程序设计的不断演进，数据结构的概念逐渐形成并得到广泛应用。这些不同阶段的发展为程序设计者提供了丰富的工具和技术，使得他们能够更好地组织和处理数据，并设计出高效的算法和程序。

何为算法

算法是指解决特定问题的一系列清晰而有限的指令或步骤，这些指令描述了如何在有限时间内完成任务或达成目标。算法可以用来处理各种计算问题，从简单的数学计算到复杂的数据处理和优化任务。

一个算法通常由输入、输出和处理三个部分组成。输入是指问题的初始数据，输出是指解决问题后得到的结果，处理则是指将输入转换为输出的具体步骤。

一个好的算法应该满足以下几个条件：

1. 正确性：算法应该能够正确地解决问题，即产生正确的输出结果。

2. 可读性：算法应该易于理解和阅读，使得其他人能够理解和使用它。

3. 高效性：算法应该在合理的时间内完成任务，即具有高效的时间和空间复杂度。

4. 健壮性：算法应该能够处理各种异常情况，如输入数据的错误或不完整等。

算法在计算机科学中扮演着非常重要的角色，因为它们是计算机程序的核心。无论是编写操作系统、设计网络协议、开发应用程序还是创建游戏，都需要使用算法来实现。因此，学习算法是计算机科学教育中的重要组成部分。

数据结构基础

基本概念和术语

数据：数据是指描述事物的符号或信息。数据不仅仅包括了整形，浮点数等数值类型，还包括了字符甚至声音，视频，图像等非数值的类型。

数据元素：数据元素是数据的基本单位，通常作为一个整体进行处理。例如，一个整数、一个字符或一个对象都可以是一个数据元素。

数据项：数据项是数据元素中的最小单位，它是数据的不可分割的基本单位。例如，一个整数中的每个数字就是一个数据项。

数据对象：是性质相同的一类数据元素的集合，是数据的一个子集。数据对象可以是有限的，也可以是无限的。

数据结构：主要是指数据和关系的集合，数据指的是计算机中需要处理的数据，而关系指的是这些数据相关的前后逻辑，这些逻辑与计算机储存的位置无关，其主要包含以下的四大逻辑结构。

四大逻辑结构（Logic Structure）

1、线性结构：线性结构中的数据元素之间存在一对一的关系，即每个数据元素只有一个直接前驱和一个直接后继。常见的线性结构包括数组、链表、栈和队列。

如图:

2、树形结构：树形结构中的数据元素之间存在一对多的关系，即每个数据元素可以有多个直接后继。常见的树形结构包括二叉树、堆和哈夫曼树。

如图：

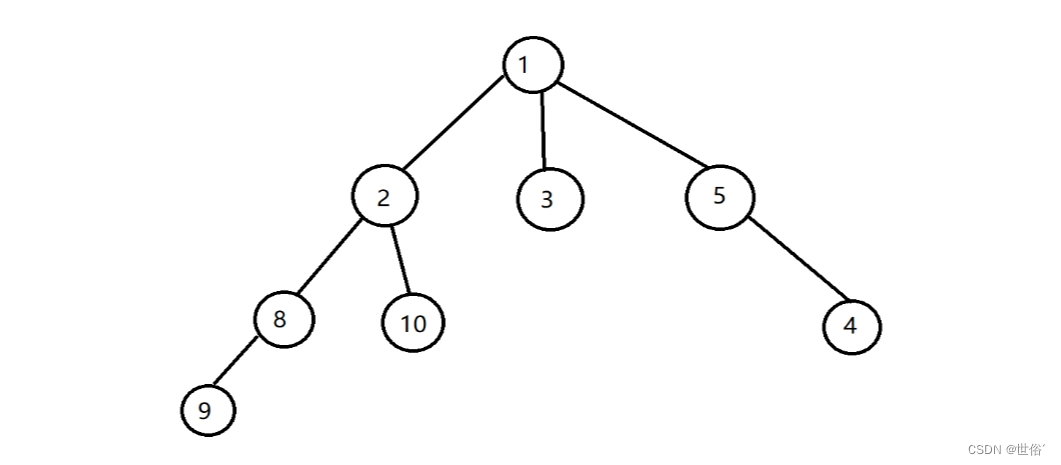
3、图形结构：图形结构中的数据元素之间存在多对多的关系，即每个数据元素可以与多个其他元素相连。常见的图形结构包括有向图和无向图。

如图：

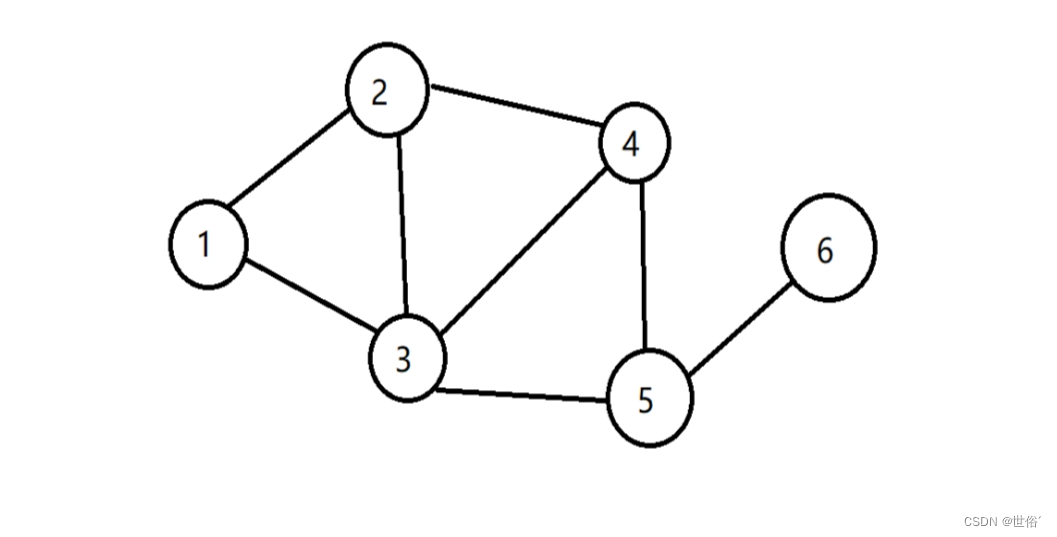
4、集合结构：集合结构中的数据元素之间没有任何特殊的关系，是相互独立的。常见的集合结构包括哈希表和并查集。

如图：

数据类型

1、数据类型

数据类型（Data Type）是高级程序设计语言中的概念，是数据的取值范围和对数进行操作的总和。数据类型规定了程序中对象的特性。程序中的每一个变量，常量或者表达式都属于一种数据类型。

2、抽象数据类型

抽象数据类型是一种概念上的定义，用于描述数据的逻辑结构和操作。它将数据的表示和操作细节隐藏起来，只暴露出对外的接口，使得使用者只需要关注数据的功能而不需要了解具体的实现细节。

抽象数据类型可以看作是一种数据的模板或者蓝图，它定义了数据的取值范围以及对数据进行的操作。通过定义一组操作，可以对数据进行增删改查等操作，而不必关心具体的实现方式。

举个例子，我们可以定义一个抽象数据类型叫做"栈"，它可以包含以下操作：

push：将一个元素压入栈顶
pop：从栈顶弹出一个元素
top：获取栈顶元素的值
isEmpty：判断栈是否为空
size：获取栈的大小

通过这些操作，我们可以在程序中使用栈这个抽象数据类型来实现各种功能，比如实现括号匹配、逆序输出等。

抽象数据类型的优点在于它提供了高度的封装性和抽象性，使得程序的设计更加模块化和可维护。同时，它也提供了良好的接口定义，使得不同的实现可以替换而不影响使用者的代码。

总之，抽象数据类型是对数据的抽象和封装，定义了数据的取值范围和操作集合，通过隐藏实现细节，提供了高度的模块化和可维护性。它在程序设计中起到了重要的作用，帮助我们更好地组织和管理数据。

理解复杂度概念

时间空间复杂度定义

1、时间复杂度（Time Complexity）是衡量算法执行时间随输入规模增长而增加的度量。它表示算法执行所需的操作次数或时间，通常用大O符号（O）来表示。

时间复杂度描述了算法执行时间与输入规模之间的关系，即算法的运行时间如何随着输入规模的增加而增长。它不是指具体的执行时间，而是一种相对的度量，用于比较不同算法的效率。

常见的时间复杂度有以下几种：

常数时间复杂度 O(1)：无论输入规模大小，算法的执行时间都保持不变。例如，访问数组中的某个元素。
线性时间复杂度 O(n)：算法的执行时间与输入规模成线性关系。例如，遍历一个数组。
对数时间复杂度 O(log n)：算法的执行时间与输入规模的对数成正比。例如，二分查找算法。
平方时间复杂度 O(n^2)：算法的执行时间与输入规模的平方成正比。例如，嵌套循环遍历一个二维数组。
指数时间复杂度 O(2^n)：算法的执行时间与输入规模的指数成正比。例如，穷举搜索算法。

综上可以得出：

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)

2、空间复杂度（Space Complexity）是衡量算法所需的额外空间随输入规模增长而增加的度量。它表示算法执行期间所占用的内存空间，通常也用大O符号（O）来表示。

空间复杂度描述了算法所需的额外空间与输入规模之间的关系，即算法的空间使用如何随着输入规模的增加而增长。

常见的空间复杂度有以下几种：

常数空间复杂度 O(1)：算法所需的额外空间不随输入规模的增加而增加，空间使用保持不变。
线性空间复杂度 O(n)：算法所需的额外空间与输入规模成线性关系。例如，需要存储一个数组或链表。
对数空间复杂度 O(log n)：算法所需的额外空间与输入规模的对数成正比。例如，递归算法的调用栈空间。
平方空间复杂度 O(n^2)：算法所需的额外空间与输入规模的平方成正比。例如，二维数组存储。

需要注意的是，时间复杂度和空间复杂度是相对的概念，它们描述了算法执行时间和空间使用随输入规模变化的趋势，并不是精确的执行时间和空间占用量。在分析算法时，我们通常关注最坏情况下的时间复杂度和空间复杂度，以评估算法的效率和资源消耗。

度量时间复杂度的方法

度量时间复杂度的常用方法是：基于函数调用次数的方法和基于语句执行次数，基于算法复杂度分析的方法。

1、基于函数调用次数的方法：这种方法通过分析算法中函数或递归调用的次数来度量时间复杂度。它通常适用于递归算法或包含循环结构的算法。具体步骤如下：

根据算法的逻辑，确定算法中涉及的函数或递归调用。
分析每个函数或递归调用的执行次数与输入规模之间的关系。
根据函数调用次数的增长趋势，得出算法的时间复杂度。

例如，对于递归实现的斐波那契数列算法：

int fibonacci(int n) {if (n <= 1)return n;elsereturn fibonacci(n - 1) + fibonacci(n - 2);
}

可以观察到，每次递归调用会导致两次更小规模的递归调用。因此，递归调用次数与输入规模呈指数关系，时间复杂度可以表示为O(2^n)。

2、基于语句执行次数的方法：这种方法通过分析算法中各个语句的执行次数来度量时间复杂度。它适用于没有函数调用或循环结构的简单算法。具体步骤如下：

根据算法的逻辑，确定算法中涉及的各个语句。
分析每个语句的执行次数与输入规模之间的关系。
根据语句执行次数的增长趋势，得出算法的时间复杂度。

例如，对于以下求和算法：

int sum(int n) {int result = 0;for (int i = 1; i <= n; i++) {result += i;}return result;
}

循环语句的执行次数与输入规模n成线性关系，因此时间复杂度可以表示为O(n)。

3、基于算法复杂度分析：该方法通过分析算法中执行次数最多的语句来度量时间复杂度。通常情况下，算法中执行次数最多的语句是循环语句。因此，我们可以通过分析循环语句的执行次数来确定算法的时间复杂度。
例如，对于以下求幂算法：

double power(double x, int n) {double result = 1.0;for (int i = 0; i < n; i++) {result *= x;}return result;
}

循环语句的执行次数与输入规模n成线性关系，因此时间复杂度可以表示为O(n)。

这三种方法都是常用的度量时间复杂度的方式，选择哪种方法取决于算法的特点和分析的需求。在实际应用中，我们通常使用基于语句执行次数的方法来分析算法的时间复杂度，因为它更直观和简单。但对于一些复杂的递归算法，基于函数调用次数的方法可能更适用。

程序运行时的内存与地址

内存是计算机中用于存储数据和指令的地方，每个内存单元都有一个唯一的地址用于访问其中的数据。通过地址，我们可以直接读取和修改内存中的数据。

在C语言中，指针是一种特殊的变量类型，它存储了一个内存地址。指针的存在使得我们可以通过间接访问内存地址来操作数据，这给编程带来了很大的灵活性。通过指针，我们可以动态分配内存、传递参数、遍历数据结构等。

首先请看这么一张图：

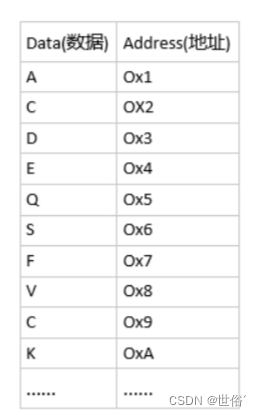
(地址的常用表示为十六进制表示法，即Ox+十六进制数)

由这个图可以清晰的发现对于每一段的内存中的数据，都有一个地址与之相对应，也真是因为有地址的存在，我们计算机中才可以轻易的去访问到其中数据，拿一个数组来说，数组在C语言中是顺序存储的，因此，如上图的数据直接用代码找到其数据以及地址的话可以这样写

#include<stdio.h>
int main(){int i;char array[10]="ACDEQSFVCK";for(i=0;i<10;i++){printf("The %c Address is %x \n",array[i],&array[i]);//%x可以换成%p都是十六进制表示，只不过%p会把所有的位数显示出来}return 0;
}

在代码示例中，使用了数组和指针来展示数据在内存中的地址。数组在C语言中是一段连续存储的数据，通过下标可以访问到对应的元素。通过取地址运算符&，我们可以获取数组元素的内存地址。指针变量可以存储这些地址，并通过解引用操作符*来访问或修改该地址处的值。

需要注意的是，不同类型的数据在内存中占用的空间大小是不同的，所以对应的地址也会有所差异。例如，char类型通常占用1字节，而int类型通常占用4字节。因此，当将char数组转换为int数组时，每个元素的地址会相应地增加4个字节。

指针的灵活性和强大功能使其成为C语言的重要特性，但同时也需要小心使用，因为错误的指针操作可能导致内存泄漏、段错误等问题。在编写代码时，应该注意正确地分配和释放内存，并避免悬空指针和越界访问等问题。

编程预备

1、malloc函数是C语言中用于动态分配内存空间的函数，它在堆中申请一块指定大小的连续内存空间，并返回该内存空间的起始地址。malloc函数的原型如下：

void* malloc(size_t size);

其中，size_t是一个无符号整数类型，在stdlib.h头文件中定义。malloc函数接受一个参数size，表示需要分配的内存空间的大小（以字节为单位）。如果内存分配成功，则返回指向分配内存的指针；如果分配失败，则返回空指针NULL。

在使用malloc函数时，需要注意以下几点：

在调用malloc函数之后，应该检查返回的指针是否为NULL，以判断内存分配是否成功。如果malloc返回NULL，则表示内存分配失败。
分配的内存空间在使用完毕后，应该通过调用free函数来释放，以便将内存返还给系统。否则，会导致内存泄漏问题。

free函数用于释放通过malloc函数分配的内存空间。free函数的原型如下：

void free(void* ptr);

其中，ptr是一个指向待释放内存空间的指针。调用free函数后，该指针所指向的内存空间将被释放，并可以被其他程序重新使用。需要注意的是，ptr必须是通过malloc、calloc或realloc函数返回的指针，或者是空指针NULL。如果ptr不满足这些条件，调用free函数将导致未定义的行为。

在使用free函数时，需要注意以下几点：

只能释放通过malloc、calloc或realloc函数分配的内存空间，否则会导致未定义的行为。
释放内存后，应该将指针设置为NULL，以避免成为野指针。

总结来说，malloc和free是C语言中用于动态分配和释放内存空间的重要函数。合理地使用这两个函数可以避免内存泄漏和野指针等问题，提高程序的效率和稳定性。

下面是一个使用malloc和free函数的代码示例，用于动态分配一个int类型的数组，并对其进行赋值和释放：

#include <stdio.h>
#include <stdlib.h>int main() {int n = 5;  // 数组大小int *arr = (int*) malloc(n * sizeof(int));  // 动态分配内存空间if (arr == NULL) {  // 判断内存分配是否成功printf("Memory allocation failed.\n");exit(1);}for (int i = 0; i < n; i++) {  // 对数组进行赋值arr[i] = i + 1;}for (int i = 0; i < n; i++) {  // 输出数组元素printf("%d ", arr[i]);}printf("\n");free(arr);  // 释放内存空间arr = NULL;  // 将指针设置为NULL，避免成为野指针return 0;
}

输出结果：