经典目标检测和最新目标跟踪都用到了RPN(region proposal network),锚框(anchor)是RPN的基础,感受野(receptive field, RF)是anchor的基础。本文介绍感受野及其计算方法,和有效感受野概念。
1.感受野概念
在典型CNN结构中,FC层(全连接层,FC layer)每个输出节点的值都依赖FC层所有输入,而CONV层(卷积层,Convolutional Layer)每个输出节点的值仅依赖CONV层输入的一个区域,这个区域之外的其他输入值都不会影响输出值,该区域就是感受野。
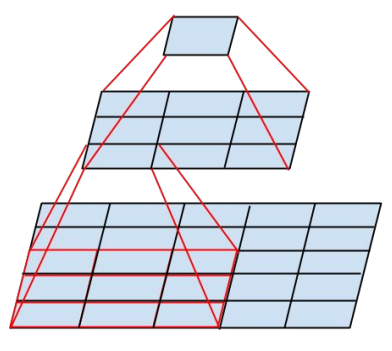
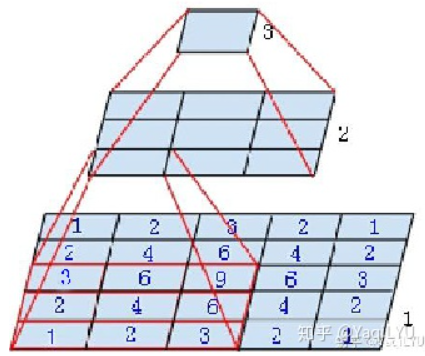
图中是个微型CNN,来自Inception-v3论文(Rethinking the Inception Architecture for Computer Vision),原图是为了说明一个conv5x5可以用两个conv3x3代替,从下到上称为第1, 2, 3层:
- 第2层左下角的值,是第1层左下红框中3x3区域的值经过卷积,也就是乘加运算计算出来的,即第2层左下角位置的感受野是第1层左下红框区域
- 第3层唯一值,是第2层所有3x3区域卷积得到的,即第3层唯一位置的感受野是第2层所有3x3区域
- 第3层唯一值,是第1层所有5x5区域经过两层卷积得到的,即第3层唯一位置的感受野是第1层所有5x5区域
就是这么简单,某一层feature map(特性图)中某个位置的特征向量,是由前面某一层固定区域的输入计算出来的,那这个区域就是这个位置的感受野。任意两个层之间都有位置—感受野对应关系,但我们更常用的是feature map层到输入图像的感受野,如目标检测中我们需要知道feature map层每个位置的特征向量对应输入图像哪个区域,以便我们在这个区域中设置anchor,检测该区域内的目标。
感受野区域之外图像区域的像素不会影响feature map层的特征向量,所以我们不太可能让CNN仅依赖某个特征向量去找到其对应输入感受野之外的目标。这里说“不太可能”而不是“绝无可能”,是因为CNN很强大,且图像像素之间有相关性,有时候感受野之外的目标是可以猜出来的,什么一叶知秋,管中窥豹,见微知著之类,对CNN目标检测都是有可能的,但猜出来的结果并不总是那么靠谱。
感受野有什么用呢?
- 一般task要求感受野越大越好,如图像分类中最后卷积层的感受野要大于输入图像,网络深度越深感受野越大性能越好
- 密集预测task要求输出像素的感受野足够的大,确保做出决策时没有忽略重要信息,一般也是越深越好
- 目标检测task中设置anchor要严格对应感受野,anchor太大或偏离感受野都会严重影响检测性能
2.感受野计算
我们首先介绍一种从后向前计算方法,极其简单适合人脑计算,看看网络结构就知道感受野了,之后介绍一种通用的从前往后计算方法,比较规律适合电脑计算,简单编程就可以计算出感受野大小和位置。
感受野是一个矩形区域,如果卷积核全都长宽相等,则对应感受野就是正方形区域。输出feature map中每个位置都对应输入图像一个感受野区域,所有位置的感受野在输入图像上以固定步进的方式平铺。
我们要计算感受野的大小r(长或宽)和不同区域之间的步进S,从前往后的方法以感受野中心(x,y)的方式确定位置,从后往前的方法以等效padding P的方式确定位置。CNN的不同卷积层,用k表示卷积核大小,s表示步进(s1表示步进是1,s2表示步进是2),下标表示层数。
从后往前的计算方式的出发点是:一个conv5x5的感受野等于堆叠两个conv3x3,反之两个堆叠的conv3x3感受野等于一个conv5x5,推广之,一个多层卷积构成的FCN感受野等于一个conv rxr,即一个卷积核很大的单层卷积,其kernelsize=r,padding=P,stride=S。
(如果我们将一个Deep ConvNet从GAP处分成两部分,看成是FCN (全卷积网络)+MLP (多层感知机),从感受野角度看FCN等价于一个单层卷积提取特征,之后特征经MLP得到预测结果,这个单层卷积也就比Sobel复杂一点,这个MLP可能还没SVM高端,CNN是不是就没那么神秘了~)
以下是一些显(bu)而(hui)易(zheng)见(ming)的结论:
- 初始feature map层的感受野是1
- 每经过一个convkxk s1的卷积层,感受野 r = r + (k - 1),常用k=3感受野 r = r + 2, k=5感受野r = r + 4
- 每经过一个convkxk s2的卷积层或max/avg pooling层,感受野 r = (r x 2) + (k -2),常用卷积核k=3, s=2,感受野 r = r x 2 + 1,卷积核k=7, s=2, 感受野r = r x 2 + 5
- 每经过一个maxpool2x2 s2的max/avg pooling下采样层,感受野 r = r x 2
- 特殊情况,经过conv1x1 s1不会改变感受野,经过FC层和GAP层,感受野就是整个输入图像
- 经过多分枝的路径,按照感受野最大支路计算,shotcut也一样所以不会改变感受野
- ReLU, BN,dropout等元素级操作不会影响感受野
- 全局步进等于经过所有层的步进累乘,S = s-1 x s-2 x s-3 x s-4
- 经过的所有层所加padding都可以等效加在输入图像,等效值P,直接用卷积的输入输出公式fout = (fin - r + 2P) / S+1 反推出P即可
这种计算方法有多简单呢?我们来计算目标检测中最常用的两个backbone的感受野。最初版本SSD和Faster R-CNN的backbone都是VGG-16,结构特点卷积层都是conv3x3s1,下采样层都是maxpool2x2s2。先来计算SSD中第一个feature map输出层的感受野,结构是conv4-3 backbone + conv3x3 classifier (为了写起来简单省掉了左边括号):
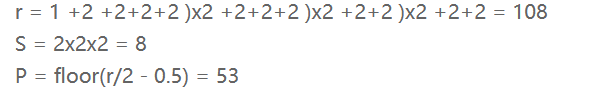
以上结果表示感受野的分布方式是:在paddding=53(上下左右都加) 的输入224x224图像上,大小为108x108的正方形感受野区域以stride=8平铺。
再来计算Faster R-CNN中conv5-3+RPN的感受野,RPN的结构是一个conv3x3+两个并列conv1x1:
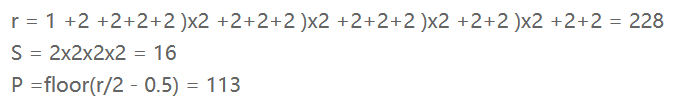
分布方式为在paddding=113的输入224x224图像上,大小为228x228的正方形感受野区域以stride=16平铺。
接下来是Faster R-CNN+++和R-FCN等采用的重要backbone的ResNet,常见ResNet-50和ResNet-101,结构特点是block由conv1x1+conv3x3+conv1x1构成,下采样block中conv3x3 s2影响感受野。先计算ResNet-50在conv4-6 + RPN的感受野 (为了写起来简单堆叠卷积层合并在一起):

P不是整数,表示conv7x7 s2卷积有多余部分。分布方式为在paddding=149的输入224x224图像上,大小为299x299的正方形感受野区域以stride=16平铺。
ResNet-101在conv4-23 + RPN的感受野:

分布方式为在paddding=421的输入224x224图像上,大小为843x843的正方形感受野区域以stride=16平铺。
以上结果都可以反推验证,并且与后一种方法结果一致。从以上计算可以发现一些的结论:
- 步进1的卷积层线性增加感受野,深度网络可以通过堆叠多层卷积增加感受野
- 步进2的下采样层乘性增加感受野,但受限于输入分辨率不能随意增加
- 步进1的卷积层加在网络后面位置,会比加在前面位置增加更多感受野,如stage4加卷积层比stage3的感受野增加更多
- 深度CNN的感受野往往是大于输入分辨率的,如上面ResNet-101的843比输入分辨率大3.7倍
- 深度CNN为保持分辨率每个conv都要加padding,所以等效到输入图像的padding非常大
前面的方法是我自用的没有出处,但后面要介绍的方法是通用的,来自一篇著名博客(需翻墙),再次强调两种方法的结果是完全一致的:
文中给出了通用的计算公式,也是逐层计算,不同点在于这里是从前往后计算,核心四个公式:
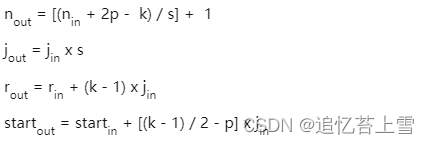
上式中n是feature map的大小,p是padding,k是kernel size,j是jump(前面的S),r是感受野大小,start是第一个特征向量(左上角位置)对应感受野的中心坐标位置。搬运并翻译:
- 公式一是通用计算卷积层输入输出特征图大小的标准公式
- 公式二计算输出特征图的jump,等于输入特征图的jump乘当前卷积层的步进s
- 公式三计算感受野大小,等于输入感受野加当前层的卷积影响因子(k - 1) * jin,注意这里与当前层的步进s没有关系
- 公式四计算输出特征图左上角位置第一个特征向量,对应输入图像感受野的中心位置,注意这里与padding有关系
从以上公式可以看出:start起始值为0.5,经过k=3, p=1时不变,经过k=5, p=2时不变
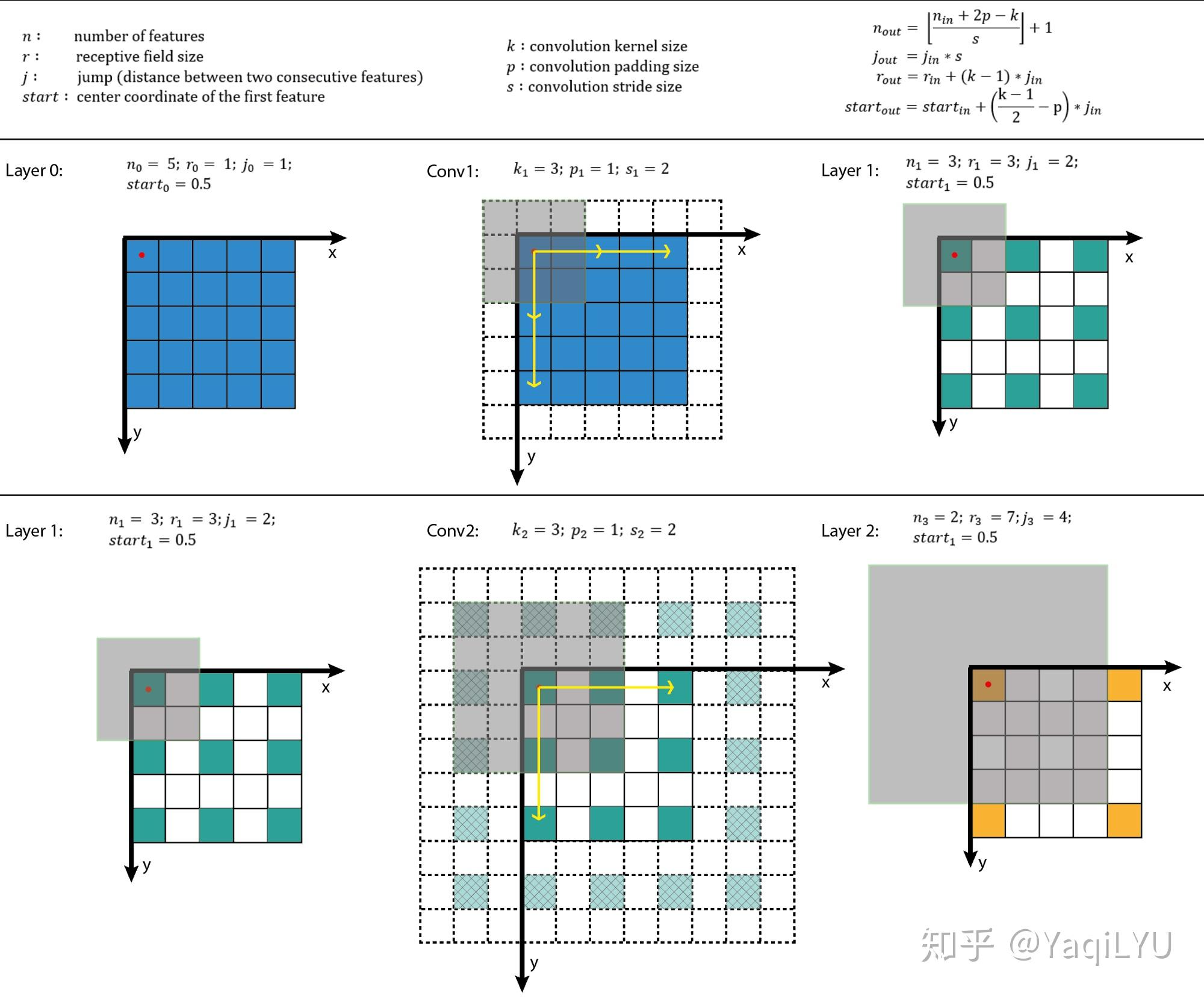
计算出r, j和start之后,所有位置感受野的大小都是r,其他位置的感受野中心是start按照j滑窗得到。这种方法比较规律,推荐编程实现。
3.有效感受野
NIPS 2016论文Understanding the Effective Receptive Field in Deep Convolutional Neural Networks提出了有效感受野(Effective Receptive Field, ERF)理论,论文发现并不是感受野内所有像素对输出向量的贡献相同,在很多情况下感受野区域内像素的影响分布是高斯,有效感受野仅占理论感受野的一部分,且高斯分布从中心到边缘快速衰减,下图第二个是训练后CNN的典型有效感受野。

这点其实也很好理解,继续回到最初那个微型CNN,我们来分析第1层,下图标出了conv3x3 s1卷积操作对每个输入值的使用次数,用蓝色数字表示,很明显越靠近感受野中心的值被使用次数越多,靠近边缘的值使用次数越少。5x5输入是特殊情况刚好符合高斯分布,3x3输入时所有值的使用次数都是1,大于5x5输入时大部分位于中心区域的值使用次数都是9,边缘衰减到1。每个卷积层都有这种规律,经过多层堆叠,总体感受野就会呈现高斯分布。
ECCV2016的SSD论文指出更好的anchar的设置应该对齐感受野:






)


之rename)
 | 传递临时对象作为线程参数的一些问题Ⅲ)



----继续学习DRV8301芯片)





