给定一个集合,枚举所有可能的子集。
(为简单起见,本文讨论的集合中没有重复元素)
1、方法一:增量构造法
第一种思路是一次选出一个元素放到集合中,程序如下:
void print_subset(int n, int *A, int cur) {for (int i = 0; i < cur; i++) printf("%d ", A[i]);printf("\n");int s = cur ? A[cur - 1] + 1 : 0; //确定当前元素的最小可能值for (int i = s; i < n; i++) {A[cur] = i;print_subset(n, A, cur + 1); //递归构造子集}
}
由于 A 中的元素个数不确定,每次递归调用都要输出当前集合。另外,递归边界也不需要显式确定——如果无法继续添加元素,自然就不会再递归了。
该代码用到了定序的技巧:规定集合 A 中所有元素的编号从小到大排列,就不会把集合 {1, 2} 按照 {1, 2} 和 {2, 1} 输出两次了。
提示:在枚举子集的增量法中,需要使用定序的技巧,避免同一个集合枚举两次。
这棵解答树上有 1024 个节点:每个可能的 A 都对应一个结点,而 n n n 元素集合恰好有 2 n 2 ^n 2n 个子集,210 = 1024。
代码
// {0~n-1}的所有子集:增量构造法
#include<cstdio>
using namespace std;void print_subset(int n, int* A, int cur) {for(int i = 0; i < cur; i++) printf("%d ", A[i]); // 打印当前集合 printf("\n");int s = cur ? A[cur-1]+1 : 0; // 确定当前元素的最小可能值for(int i = s; i < n; i++) {A[cur] = i;print_subset(n, A, cur+1); // 递归构造子集}
}int A[10];
int main() {int n;scanf("%d", &n);print_subset(n, A, 0);return 0;
}
2、方法二:位向量法
第二种思路是构造一个位向量 B[i],而不是直接构造子集 A 本身,其中 B[i] = 1,当且仅当 i 在子集 A 中。递归实现如下:
void print_subset(int n, int *B, int cur) {if (cur == n) {for (int i = 0; i < cur; i++) {if (B[i]) printf("%d ", i); //打印当前集合}printf("\n");return ;}B[cur] = 1; //选第cur个元素print_subset(n, B, cur + 1);B[cur] = 0; //不选第cur个元素print_subset(n, B, cur + 1);
}
必须当 “所有元素是否选择” 全部确定完毕后才是一个完整的子集,因此当 if (cur == n) 成立时才输出。
现在的解答树上有 2047 个结点,比刚才的方法略多,因为所有部分解(不完整解)也对应着解答树上的结点。
提示:在枚举子集的位向量法中,解答树的节点数略多,但在多数情况下仍然够快。
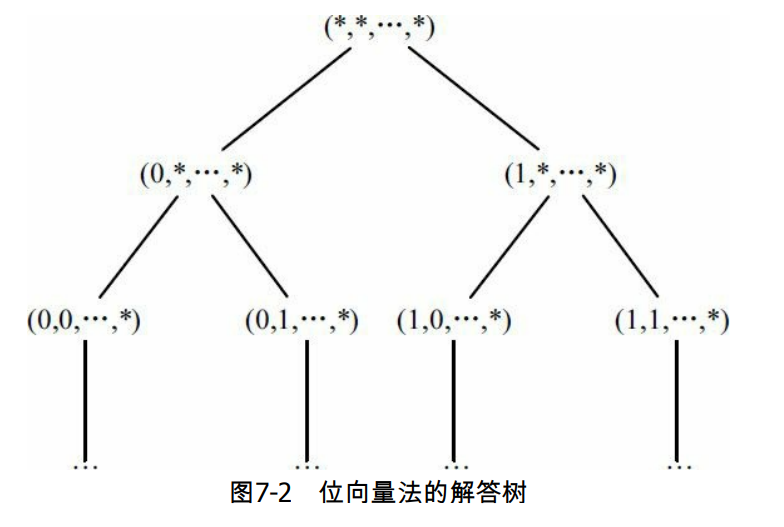
这是一棵 n + 1 n+1 n+1 层的二叉树(cur 的范围0 ~ n),第0层有1个结点,第1层有2个结点,第2层有4个结点,第3层有8个结点,…,第 i i i 层有 2 i 2^i 2i 个结点,总数为 1 + 2 + 4 + 8 + . . . + 2 n = 2 n + 1 − 1 1 + 2 + 4 + 8 + ... + 2^n = 2^{n+1} - 1 1+2+4+8+...+2n=2n+1−1,和实验结果一致。
下图为这棵解答树。
代码
// {0~n-1}的所有子集:位向量法
#include<cstdio>
using namespace std;void print_subset(int n, int* B, int cur) {if(cur == n) {for(int i = 0; i < cur; i++)if(B[i]) printf("%d ", i); // 打印当前集合printf("\n");return;}B[cur] = 1; // 选第cur个元素print_subset(n, B, cur+1);B[cur] = 0; // 不选第cur个元素print_subset(n, B, cur+1);
}int B[10];
int main() {int n;scanf("%d", &n);print_subset(5, B, 0);return 0;
}
3、方法三:二进制法
还可以用二进制来表示 {0,1, 2,…,n - 1} 的子集 S:从右往左第 i i i 位(各位从0开始编号)表示元素 i i i 是否在集合 S 中。下图展示了二进制 0100011000110111是如何表示集合{0,1,2,4,5,9,10,14} 的。
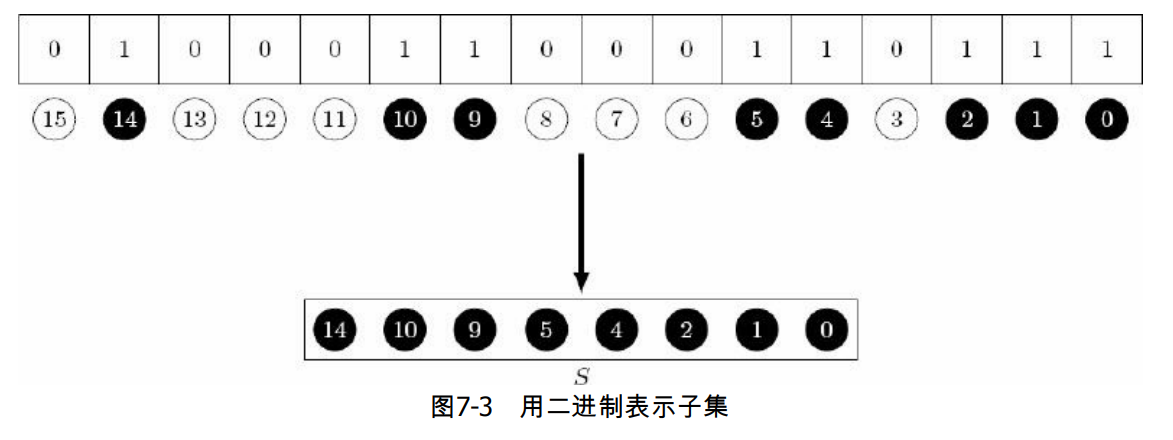
注意:为了处理方便,最右边的位总是对应元素0,而不是元素1。
提示:可以用二进制表示子集,其中从右往左第 i i i 位(从0开始编号)表示元素 i i i 是否在集合中(1表示“在”,0表示“不在”)。
表示出集合后,还要对集合进行操作。常见的集合运算都可以用位运算符简单实现。最常见的二元运算符是与(&)、或(|)、非(!),它们和对应的逻辑运算非常相似,如下表所示。
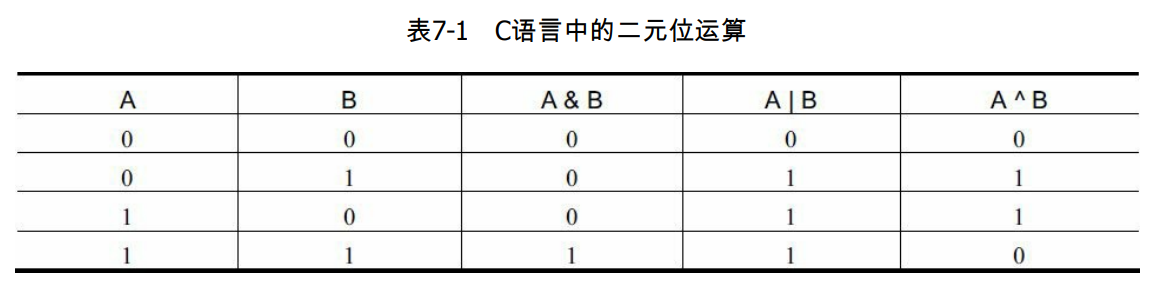
“异或(XOR)”运算符“^",其规则是 “如果 A 和 B 不相同,在 A ^ B = 1,否则为0”。异或运算最重要的性质就是“开关性”——异或两次以后相当于没有异或,即 A^B^B = A。另外,与、或和异或都满足交换律:A&B = B&A,A|B = B|A,A^B = B^A。
与逻辑运算符不同的是,位运算符(bitwise operator)是逐位进行的——两个 32 位整数的"按位与" 相当于 32 对 0/1 值之间的运算。下表比欧式了二进制数10110(十进制22)和01100(十进制12)之间的按位与、按位或、按位异或的值,以及对应的集合运算的含义。
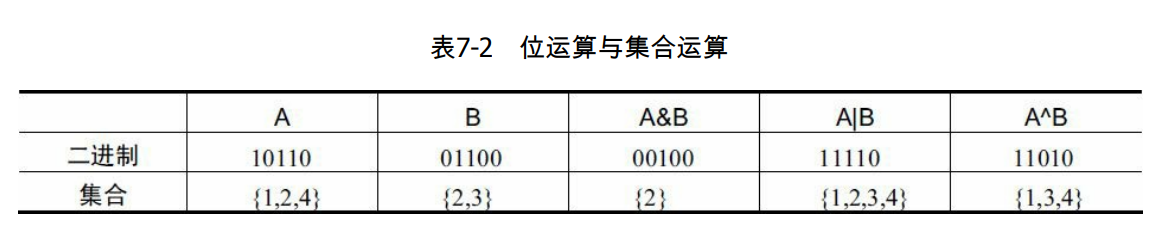
可见,A&B、A|B 和 A^B 分别对应集合的交、并和对称差。另外,空集为0,全集{0, 1, 2, …, n − 1 n-1 n−1} 的二进制为 n n n 个 1,即十进制 2 n − 1 2^n - 1 2n−1。为了方便,往往在程序中把全集定义为 ALL_BITS = (1 << n) - 1,则 A 的补集就是ALL_BITS^A。 当然,直接用整数减法ALL_BITS - A 也可以,但速度比位运算 “^” 慢。
提示:当用二进制表示子集时,位运算中的按位与、或、异或对应集合的交、并和对称差。
如此,就可以用下面的程序输出子集 S 对应的各个元素:
void print_subset(int n, int s) { //打印 {0, 1, 2, ..., n-1} 的子集Sfor (int i = 0; i < n; i++) {if (s & (1 << i)) printf("%d ", i); //利用了C语言“非0值都为真”的规定}printf("\n");
}
而枚举子集和枚举整数一样简单:
for (int i = 0; i < (1 << n); i++) { //枚举各子集所对应的编码0, 1, 2, ..., 2^n - 1print_subset(n, i);
}
代码
// {0~n-1}的所有子集:二进制法
#include<cstdio>
using namespace std;void print_subset(int n, int s) { // 打印{0, 1, 2, ..., n-1}的子集Sfor(int i = 0; i < n; i++)if(s&(1<<i)) printf("%d ", i); // 这里利用了C语言“非0值都为真”的规定printf("\n");
}int main() {int n;scanf("%d", &n);for(int i = 0; i < (1<<n); i++) // 枚举各子集所对应的编码 0, 1, 2, ..., 2^n-1print_subset(n, i);return 0;
}



)









)



|坑洼道路检测和识别|数学建模完整代码+建模过程全解全析)
:本地部署、量化及GPT-4对比)
