正则化
在机器学习学习中往往不知道需要不知道选取的特征个数,假如特征个数选取过少,容易造成欠拟合,特征个数选取过多,则容易造成过拟合。由此为了保证模型能够很好的拟合样本,同时为了不要出现过拟合现象,引入了一个正则项。
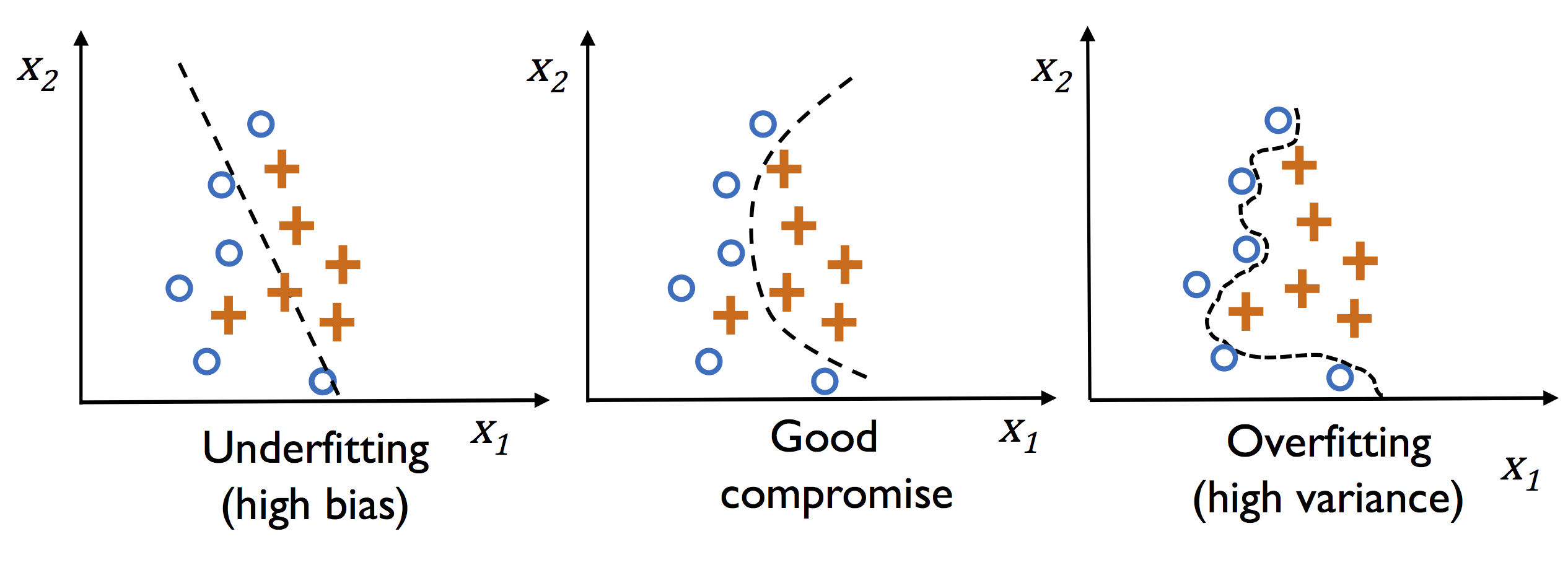
如图所示:
当选用特征过少时,函数的拟合程度如左边的图一样,不能很好的拟合
当选用特征适中时,函数的拟合程度如中间的图一样,可以比较好的拟合
当选用特征过多时,函数的拟合程度如右边的图一样,能够完全拟合样本,但是可能在测试数据上不佳。
当选用均方误差作为损失函数时
Loss function: ∑ ( y − W x i ) 2 \sum (y-Wx_i)^2 ∑(y−Wxi)2,当选择模型过于复杂时(即 W W W维度过高, X X X特征过多时)损失函数往往趋近于0甚至等于0,能够很好的拟合样本但是不具有很好的泛化能力,所以为了降低模型的复杂度我们引入了一个正则项 λ W T W \lambda W^TW λWTW。即损失函数为 ∑ ( y − W x i ) 2 + λ W T W \sum (y-Wx_i)^2+\lambda W^TW ∑(y−Wxi)2+λWTW。由此最小化损失函数时。会考虑模型的复杂度,保证模型不至于太复杂。
当存在一个样本 X = { x 1 , x 2 , ⋯ , x n } \mathbf{ X=\{x_1,x_2,\cdots,x_n\}} X={x1,x2,⋯,xn}, y = a x 2 + b x + c + ξ y=ax^2+bx+c+\xi y=ax2+bx+c+ξ,其中 ξ \xi ξ为一个高斯噪声,
当选择模型: θ 1 x + θ 2 \theta_1 x+\theta_2 θ1x+θ2时,模型无法很好的拟合样本
当选择模型: θ 1 x 2 + θ 2 x + θ 3 \theta_1 x^2+\theta_2 x+\theta_3 θ1x2+θ2x+θ3时,模型可以较好的拟合样本
当选择模型: θ 1 x 5 + θ 2 x 4 + θ 3 x 3 + θ 4 x 2 + θ 5 x + θ 6 \theta_1 x^5+\theta_2 x^4+\theta_3 x^3+\theta_4 x^2+\theta_5 x+\theta_6 θ1x5+θ2x4+θ3x3+θ4x2+θ5x+θ6时,模型可以完全拟合样本,当引入正则项 λ W T W \lambda W^TW λWTW,可以保证 W W W不至于太复杂,由此可以使 θ 1 , θ 2 , θ 3 \theta_1,\theta_2,\theta_3 θ1,θ2,θ3足够小,不至于使给模型造成太大的影响,所以可以避免模型太过于复杂以至于过拟合。












——创建PBR材质)


)
)


