目录：

八大排序算法：

超链接：
插入排序
选择排序
交换排序
归并排序
非比较排序

一、排序的概念

1.1 排序的概念

排序:所谓排序，就是使一串记录， 按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。稳定性:假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]， 且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

1.2 排序的应用

排序的目的通常是为了方便查找，或者统计最多或者最少的重复次数。
1.游戏竞赛。 游戏规则是随机一组30张图片，要求参加比赛的10人在30秒之内把图片按照从小到大顺序排序，时间最少的获胜。
2.调查问卷。 在1～10000中随机生成N个数，对于重复的数只保留一个，不同的数对应着不同学生的学号，再把这些数从小到大排序，按顺序找同学调查。
3.颁发特等奖学金。 某个大学有n名学生，每个人都有m门课，按照综合成绩排名，需要挑出最优秀的k位学生颁发特等奖学金。

二、直接插入排序

直接插入排序的基本思想：
把待排序的内容记录并逐一与排序好的有序序列比较，插入到有序序列中，直到待排序列的记录全部插入完毕，得到一个新的有序序列，这就是直接插入排序

代码如下

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <time.h>
#include <windows.h>
#define m 1000
void IsertSort(int* arr, int n)
{int i;for (i = 1; i < n; i++)//i为待排序的第一个数下标{int end = i - 1;//end 为已排好序列的尾下标int tmp = arr[i];//把待排序的第一个数存起来//遍历已排序列，进行比较然后插入，这里我进行从小到大排序while (end >= 0){if (arr[end] > tmp)//如果前面的数大，就把他往后移动一个{arr[end + 1] = arr[end];end--;}//否则就跳出elsebreak;arr[end + 1] = tmp;}}//打印排序后的数据for (i = 0; i < n; i++){printf("%d ", arr[i]);}
}
int main()
{int head, end,arr[m];//srand(初始化时间)，time(直接返回时间戳)srand((unsigned)time(NULL));head = clock();for (int i = 0; i < m; i++)arr[i] = rand();//，时间不停的变化，每次产生不同的随机值IsertSort(arr,sizeof(arr)/sizeof(arr[0]));end = clock();//排序需要花费的时间printf("\n%d\n ", end - head);return 0;
}

直接插入排序的性能总结：
1.元素集合越接近有序，直接插入排序算法的时间效率越高。
2.时间复杂度：O(N^2)
3.空间复杂度为：O(1),它是一种稳定的排序算法
4.稳定性:稳定

三、希尔排序

希尔排序又叫缩小增量法。
希尔排序的基本思想：
先选定一个整数，然后把待排序的记录分成这个整数的组，所有距离为这个整数的记录被分在同一个组，并对每一个组内的记录进行排序。先预排序，然后在插入排序。

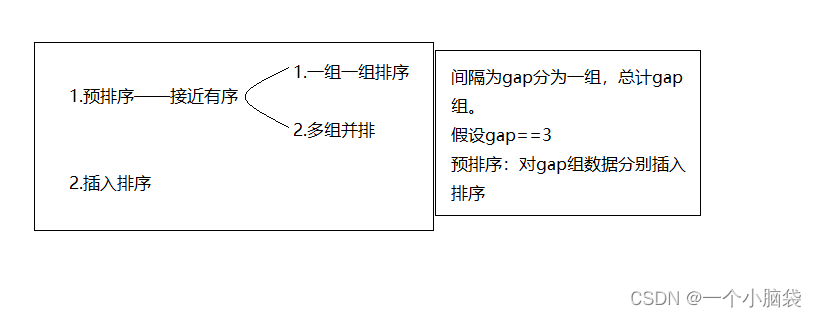
代码如下：

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include <Windows.h>
#define m 10000
SheelSort(int* arr, int n)
{int gap = 3;//多趟for(int j=0;j<gap; j++)//每组进行插入排序for (int i =j; i < n - gap; i += gap){//单趟int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] < tmp)//从大到小排序{arr[end + gap] = arr[end];end -= gap;}elsebreak;   }arr[end + gap] = tmp;}
}
int main()
{int head, tail, i;int arr[m] = {0};srand((unsigned)time(NULL));for (i = 0; i < m; i++)arr[i] = rand()%1000;head = clock();SheelSort(arr, sizeof(arr) / sizeof(arr[0]));tail = clock();printf("%d ", tail - head);return 0;
}

效率如下

我们可以优化一下(减少一个循环，但是效率还是差不多得，而且代码更简洁)：

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include <Windows.h>
#define m 10000
SheelSort_1(int* arr, int n)
{int gap = 3;//按顺序，一组一组排序for (int i = 0; i < n - gap; i ++){//单趟int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] < tmp)//从大到小排序{arr[end + gap] = arr[end];end -= gap;}elsebreak;}arr[end + gap] = tmp;}
}
int main()
{int head, tail, i;int arr[m] = {0};srand((unsigned)time(NULL));for (i = 0; i < m; i++)arr[i] = rand()%1000;head = clock();SheelSort_1(arr, sizeof(arr) / sizeof(arr[0]));tail = clock();printf("%d ", tail - head);return 0;
}

我们可以得知预排序的意义：
1.gap越大，大的数可以更快的到后面，小的数可以更快到前面，gap越大跳的越快，越不接近有序。
2.gap越小，大的小的数挪动越慢，越接近有序。
3.gap= =1，就是直接插入排序。
但是我们不知道gap取什么值最好
我们在把代码变一变，让gap无论是多少，最后都等于gap= =1.（gap >1为预排序）

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include <Windows.h>
#define m 10000
SheelSort_3(int* arr, int n)
{int gap = n;while(gap >1)//先预排序，预排序结束后，直接插入排序{gap=gap/3+1;//gap=gap/2;//按顺序，一组一组排序for (int i = 0; i < n - gap; i ++){//单趟int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] < tmp)//从大到小排序{arr[end + gap] = arr[end];end -= gap;}elsebreak;}arr[end + gap] = tmp;}}
}
int main()
{int head, tail, i;int arr[m] = {0};srand((unsigned)time(NULL));for (i = 0; i < m; i++)arr[i] = rand()%1000;head = clock();SheelSort_3(arr, sizeof(arr) / sizeof(arr[0]));tail = clock();printf("%d ", tail - head);return 0;
}

计算它的时间复杂度？

1.gap很大时gap=n / 3+1,可分为n/3组数据，每组3个元素，每组最坏的比较次数为3次所以一共：n / 3 * 3次。
2.gap很小时，gap=1，每组1个元素，很接近有序，间距为gap的这些数据，数据往后挪动的次数：n。
3.gap很大时，n / 9个组，9个元素，每组最坏比较36次。（1+2……+8），间距为gap的这些数据。合计挪动数据：n / 9* 36=4n次
4.外面那个循环运算了log3^N次
总结：合计n / gap组，每组gap个，每组插入：1+2+3+……+gap。合计：（1+gap) * gap / 2
时间复杂度O(N^1.3)最好情况

稳定性：不稳定

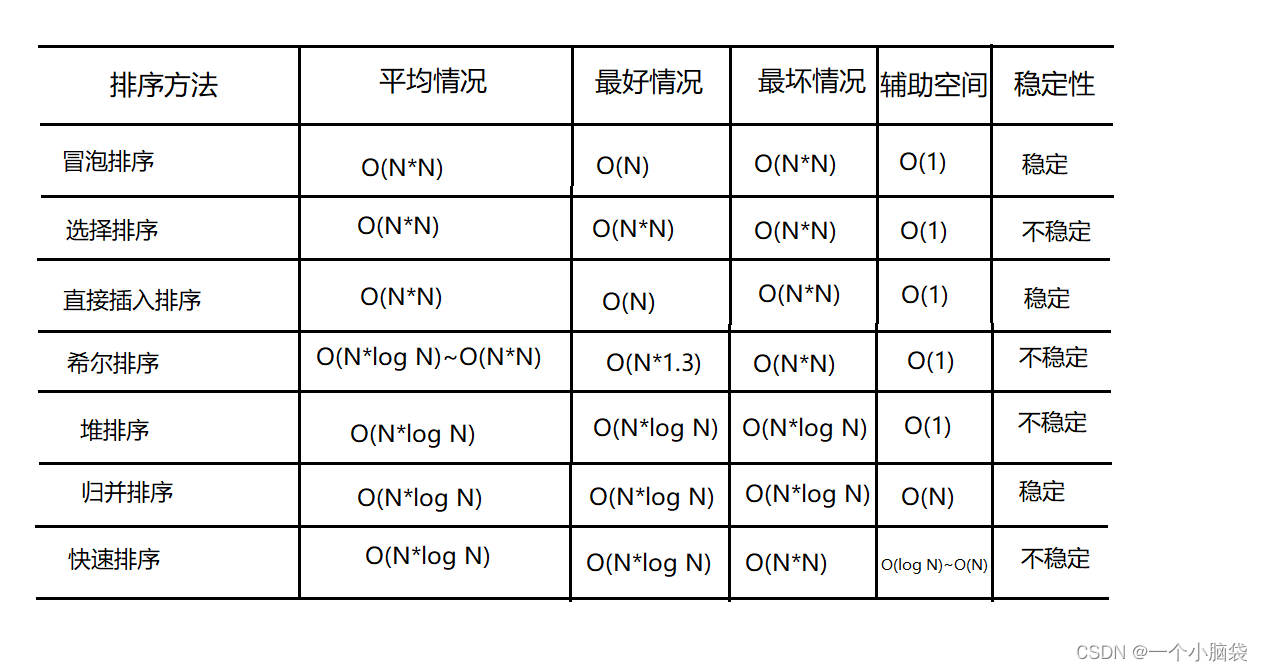
四、排序算法复杂度及稳定性分析

如图：

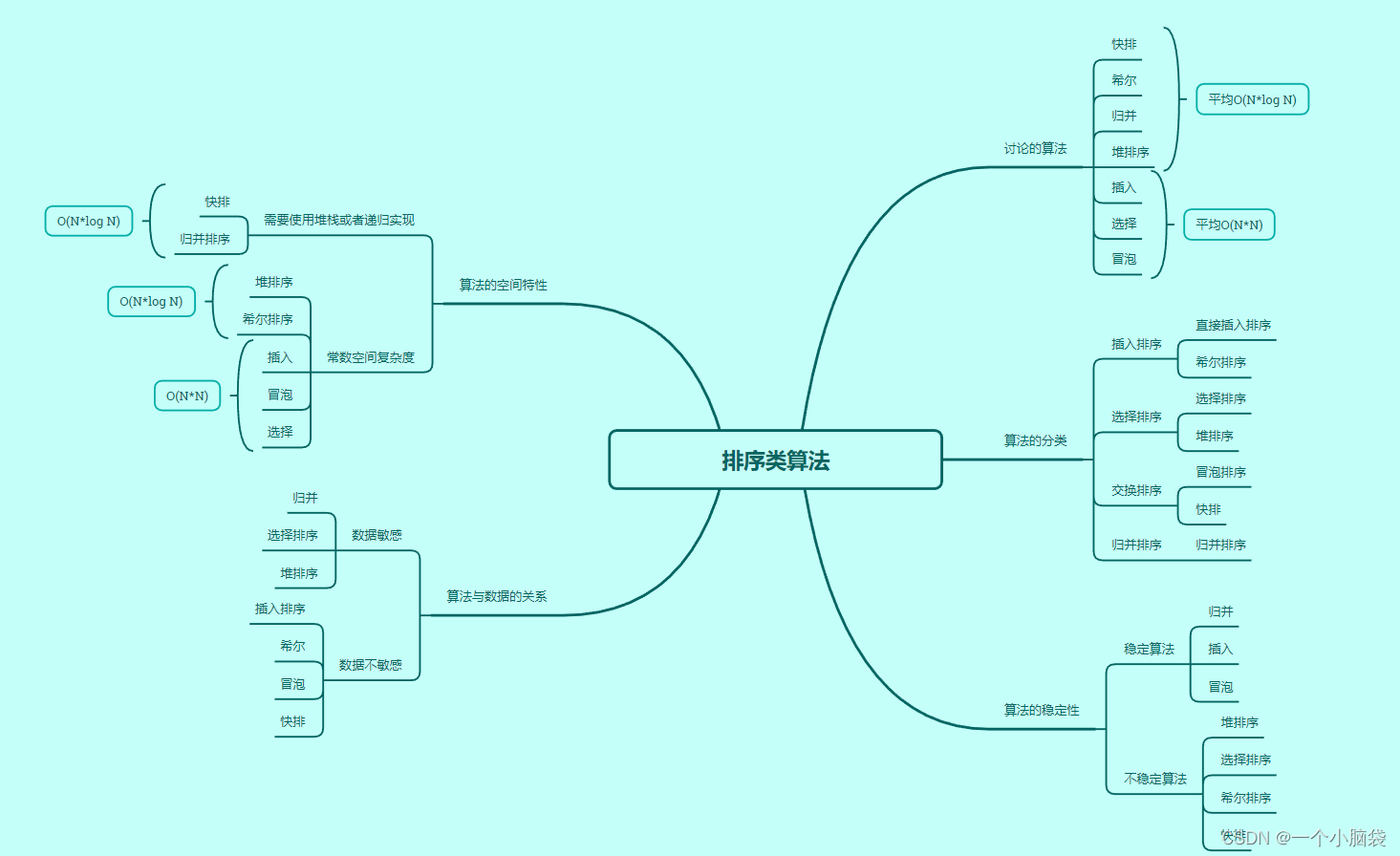
表格：