👨‍🎓作者简介：一位即将上大四，正专攻机器学习的保研er
🌌上期文章：机器学习&&深度学习——多层感知机的简洁实现
📚订阅专栏：机器学习&&深度学习
希望文章对你们有所帮助

在机器学习中，我们的目标是发现模式。但是，我们需要确定模型不只是简单记住了数据，还要确定模型真正发现了一种泛化的模式。我们的模型需要判断从未见过的情况，只有当模型发现了一种泛化模式时，才会作出有效的预测。
正式地讲，我们的目标是发现某些模式，这些模式会捕捉到我们训练集潜在总体的规律。如果成功做到这点，那么即便是以前从未遇到过的个体，模型也可以成功地评估风险。如何发现泛化模式是机器学习的根本问题。
困难在于，当我们训练模型时，只能访问数据中的小部分样本，这样可能会导致我们在收集更多数据时，可能会发现之前找到的明显关系不成立。
将模型在训练数据上拟合的比在潜在分布中更接近的现象称为过拟合，用于对抗过拟合的技术称为正则化。
而在之前用Fashion-MNIST数据集做实验时就出现了过拟合现象。在实验中调整模型架构或超参数时会发现：如果有足够多的神经元、层数和训练迭代周期，模型最终可以在训练集上达到完美的精度，此时测试集的准确性却下降了。

训练误差和泛化误差

举个例子来体会一下何为误差：
假设让模型来判断100个人里面谁最有可能下个月不还银行贷款，这时候我们的模型发现，上个月没还的五个人都穿了蓝色衣服，结果模型就把这个蓝色信息记住了，但是这其实是没有道理的，他们下个月可能穿着红衣服不还贷款。
训练误差：模型在训练数据集上计算得到的误差。
泛化误差：模型应用在同样从原始样本的分布中抽取的无限多数据样本时，模型误差的期望。
我们不能准确地计算出泛化误差，在实际中，我们只能通过将模型应用于一个独立的测试集来估计泛化误差， 该测试集由随机选取的、未曾在训练集中出现的数据样本构成。
例子：根据模考成绩预测未来考试成绩，但是过去的考试表现很好（训练误差）不代表未来考试会好（泛化误差）

统计学习理论

我们假设训练数据和测试数据都是从相同的分布中独立提取的。这通常叫作独立同分布假设，这意味着对数据进行采样的过程没有进行记忆。比如，抽取的第2个样本和第3个样本的相关性，并不比抽取的第2个样本和第200万个样本的相关性更强。
假设是存在漏洞的，假设可能会出现实效的情况。比如两个数据的分布可能不是完全一样的（用医院A的患者数据训练死亡风险预测评估，将其应用于医院B的话），又或是抽样的过程可能与时间有关（对微博主题进行分类时，新闻周期会使得正在讨论的话题产生时间依赖性，从而违反独立性假设）。
有时候我们即使轻微违背独立同分布假设，模型仍将继续运行得非常好，例如人脸识别、语音识别。几乎所有现实的应用都至少涉及到一些违背独立同分布假设的情况。
但是有时候会很麻烦，比如，我们试图只用来自大学生的人脸数据来训练一个人脸识别系统， 然后想要用它来监测老人，大学生和老年人看起来区别还是很大的。
因此，接下来将会讨论因违背独立同分布假设而引起的问题。即使认为独立同分布假设是理所当然的，理解泛化性也不容易。
当我们训练模型时，我们试图找到一个能够尽可能拟合训练数据的函数。但是如果它执行地“太好了”，而不能对看不见的数据做到很好泛化，就会导致过拟合。

模型复杂性

当我们有简单的模型和大量的数据时，我们期望泛化误差与训练误差相近。当我们有更复杂的模型和更少的样本时，我们预计训练误差会下降，但泛化误差会增大。
我们很难比较本质上不同大类的模型之间（例如，决策树与神经网络）的复杂性。目前可以用一条简单的经验法：能够轻松解释任意事实的模型是复杂的。
下面重点介绍几个倾向于影响模型泛化的因素：
1、可调整参数的数量，当可调整参数的数量（自由度）很大时，模型更容易过拟合
2、参数采用的值，当权重的取值范围较大时，模型更容易过拟合
3、训练样本的数量，即使模型很简单，也很容易过拟合只包含一两个样本的数据集，而过拟合一个有百万样本的数据集就需要非常灵活的模型了。

模型选择

通常在评估几个模型后选择最后模型，这个过程就是模型选择。有时要比较的模型本质不同，有时是同样的模型设置不同的超参数的情况下进行比较。
例如，训练多层感知机时，我们可能就希望有不同数量的隐藏层和不同数量的隐藏单元、不同的激活函数组合等等。要选出最佳模型，我们会常使用验证集。

验证集

原则上，在我们确定所有的超参数之前，我们不能用测试集。（如果过拟合了训练数据，我们可以通过测试数据来判断出来，但是如果用了测试数据来进行模型选择，要是测试数据过拟合了，我们却无从得知，只能错认为这个模型是好的）。
然而，我们也不能仅靠训练数据来选择模型，因为无从得知训练数据的泛化误差。
理想情况下我们只用测试数据一次来评估模型，但是现实中测试数据往往不会测一次就丢了，因为我们可能没有那么多的数据对每一轮的实验采用全新测试机。
解决这个问题的常见做法是把数据分为三分：训练集、测试机、验证集。多加了个验证数据集。
现实中的验证集和测试机的边界太模糊了，所以以后没有说明的情况还是尽量用验证集，准确度也是代表着验证集准确度。

K折交叉验证

训练数据太少时，我们可能无法提供足够数据来构成一个合适验证集，此时可以采用K折交叉验证。原始训练数据被分成K个不重叠的子集，然后执行K次模型训练和验证，每次在K-1个子集上进行训练，并在剩余的子集上进行验证。最后通过对K此实验的结果取平均来估计训练和验证误差。
算法如下：

·将训练数据分割成K块
·For i=1,…,K
···使用第i块作为验证数据集
·报告K个验证集误差的平均

常用K为5或10。

欠拟合还是过拟合？

如果模型不能降低训练误差，这可能意味着模型过于简单，无法捕获试图学习的模式。我们有理由相信可以用一个更复杂的模型降低训练误差，这种现象就叫做欠拟合。
而当我们的训练误差明显低于验证误差的时候要小心，这表明严重的过拟合。过拟合并不一定就是坏的。最终，我们会更关心验证误差，而不是训练误差和验证误差之间的差距。
是否过拟合或欠拟合可能取决于模型复杂性和可用训练数据集的大小，下面给出一个非常粗略的表格（行表示数据的简单或复杂，列表示模型容量的低或高）：

	简单	复杂
低	正常	欠拟合
高	过拟合	正常

估计模型容量

我们难以在不同的种类算法之间比较（如树模型和神经网络），我们可以给定一个模型种类，根据：
1、参数的个数
2、参数值的选择范围
来大致估计模型容量的大小，如图：


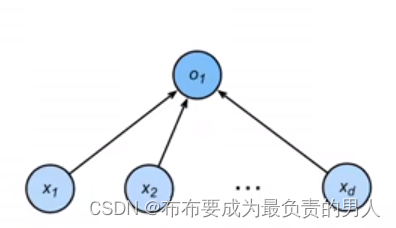
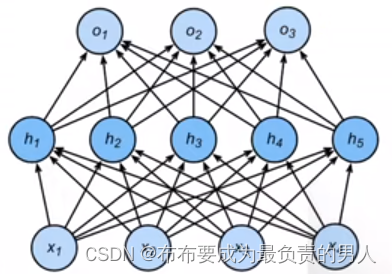
容易看出第一个参数个数为d+1个，第二个参数的个数为(d+1)m+(m+1)k个，显然后者更复杂。

模型复杂性

为了说明过拟合和模型复杂性的经典直觉，我们给出一个多项式例子，给定单个特征x和对应实数标签y组成的训练数据，视图找到下面的d阶多项式来估计标签y：
$$\hat{y}=\sum _{i=0}^d{x}^i{w}_i$$
这是一个线性回归问题，我们的特征是x的幂给出的，模型权重是w给出的，偏置是w0给出的（因为所有的x都有x的0次幂等于1）。线性回归问题，我们可以用平方误差来作为我们的损失函数。
高阶多项式函数比低阶多项式函数复杂得多。高阶多项式的参数较多，模型函数的选择范围较广。因此在固定训练数据集的情况下，高阶多项式函数相对于低阶多项式的训练误差应该始终更低（最坏也是相等）。
下图直观描述了模型复杂度（多项式阶数）和欠拟合与过拟合之间的关系：

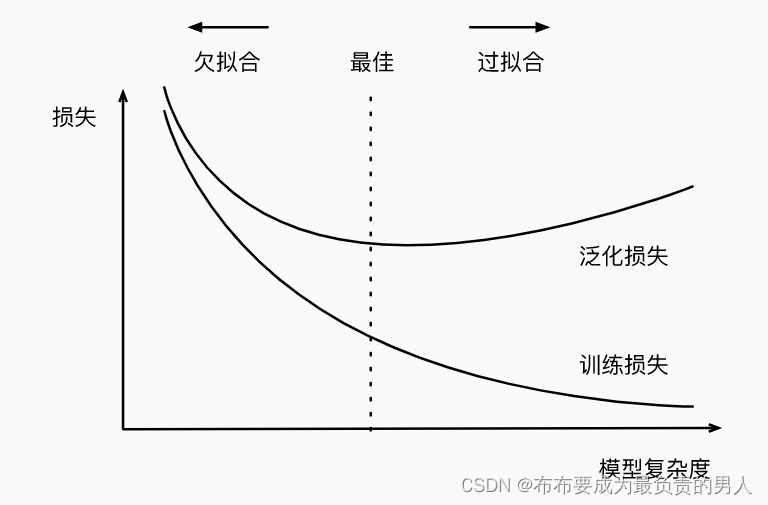
理解起来也简单：
1、对于简单的模型，拟合数据的能力很差，那么获得泛化的能力也是非常差的，这时候自然泛化误差与训练误差都很高。
2、随着模型复杂度的增大，模型能够越来越拟合训练数据，这时候我们可以认为其泛化能力也会增强，泛化损失也会降低。
3、但是如果模型复杂度过大，他记忆能力就太强了，可能会记住很多无用的噪声信息（比如之前所说的上个月不还贷款的人都穿蓝衣服，这其实是噪声项）。那这时候再去拿新数据验证的时候，就容易出现问题，因此模型复杂度太大的时候可能会导致训练误差逐渐降低的同时泛化损失反而变大。

数据集大小

另一个重要因素是数据集大小。训练数据集中的样本越少，越可能过拟合。随着训练数据量的增加，泛化误差通常会减小，一般更多的数据是不会有什么坏处的。
模型复杂性和数据集大小之间通常存在关系，给出更多的数据，我们可能会尝试拟合一个更复杂的模型；如果没有更多的数据，简单模型可能会更有用。

多项式回归

这边我们通过多项式拟合来直观感受拟合的概念。

import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l

生成数据集

给定x，我们使用以下三阶多项式来生成训练和测试数据的标签：
$$\begin{gathered} y=5+1.2x-3.4\frac{x^2}{2!}+5.6\frac{x^3}{3!}+\sigma \\ 其中\sigma 符合正态分布N(0,0.1^2) \end{gathered}$$
在优化的过程中，我们通常希望避免非常大的梯度值或损失值。这就是我们将特征从从xⁱ调整为xⁱ/i!的原因，这样可以避免很大的i带来的特别大的指数值。我们将为训练集和测试集各生成100个样本。

max_degree = 20  # 多项式的最大阶数
n_train, n_test = 100, 100  # 训练和测试数据集大小
true_w = np.zeros(max_degree)  # 分配大量的空间
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))  # 把每个features都实现x的0到19次幂的运算
for i in range(max_degree):  # 每个x的次幂都要除以其次幂的阶乘poly_features[:, i] /= math.gamma(i + 1)  # gamma(n)=(n-1)!
# labels的维度:(n_train+n_test,)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)

同样，存储在poly_features中的单项式由gamma函数重新缩放，体重gamma(n)=(n-1)!。从生成的数据集中查看一下前2个样本，第一个值是与偏置相对应的常量特征。

# Numpy ndarray转换为tensor
true_w, features, poly_features, labels = [torch.tensor(x, dtype=torch.float32) for x in [true_w, features, poly_features, labels]]print(features[:2], '\n', poly_features[:2, :], '\n', labels[:2])

tensor([[0.2813],
[1.4815]])
tensor([[1.0000e+00, 2.8131e-01, 3.9568e-02, 3.7104e-03, 2.6094e-04, 1.4681e-05,
6.8834e-07, 2.7663e-08, 9.7274e-10, 3.0405e-11, 8.5533e-13, 2.1874e-14,
5.1279e-16, 1.1096e-17, 2.2297e-19, 4.1816e-21, 7.3521e-23, 1.2166e-24,
1.9014e-26, 2.8152e-28],
[1.0000e+00, 1.4815e+00, 1.0974e+00, 5.4194e-01, 2.0072e-01, 5.9474e-02,
1.4685e-02, 3.1080e-03, 5.7556e-04, 9.4743e-05, 1.4036e-05, 1.8904e-06,
2.3339e-07, 2.6597e-08, 2.8145e-09, 2.7798e-10, 2.5739e-11, 2.2431e-12,
1.8462e-13, 1.4395e-14]])
tensor([5.3927, 6.0603])

对模型进行训练和测试

实现一个函数来评估模型在给定数据集上的损失

def evaluate_loss(net, data_iter, loss):  #@save"""评估给定数据集上模型的损失"""metric = d2l.Accumulator(2)  # 0：损失的总和，1:样本的数量for X, y in data_iter:out = net(X)  # 得到网络输出后的值（预测值）y = y.reshape(out.shape)  # 原先的值，形状要调整成一样的l = loss(out, y)  # 计算损失metric.add(l.sum(), l.numel())return metric[0] / metric[1]

下面定义一下训练函数：

def train(train_features, test_features, train_labels, test_labels,num_epochs=400):loss = nn.MSELoss(reduction='none')  # 对于线性模型，我们直接使用MSELoss均方误差损失input_shape = train_features.shape[-1]  # shape[-1]表示读取最后一个维度的长度，其实在这里就等价于shape[1]，因为只有2个维度# 不设置偏置，因为我们已经在多项式中就实现了它net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))batch_size = min(10, train_labels.shape[0])train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)),batch_size)test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)),batch_size, is_train=False)  # 把is_train设为False就代表是测试的trainer = torch.optim.SGD(net.parameters(), lr=0.01)animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',xlim=[1, num_epochs], ylim=[1e-3, 1e2],legend=['train', 'test'])for epoch in range(num_epochs):d2l.train_epoch_ch3(net, train_iter, loss, trainer)if epoch == 0 or (epoch + 1) % 20 == 0:animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),evaluate_loss(net, test_iter, loss)))print('weight:', net[0].weight.data.numpy())

三阶多项式函数拟合（正常）

首先使用三阶多项式函数，这与数据生成函数的阶数是相同的。结果表明该模型可以有效降低训练损失与测试损失。且学习到的模型参数也接近真实值。

# 从多项式特征中选择前4个维度，也就是x^0,x^2/2!,x^3/3!
train(poly_features[:n_train, :4], poly_features[n_train:, :4],labels[:n_train], labels[n_train:])
d2l.plt.show()

输出值：

weight: [[ 4.9961195 1.220384 -3.417343 5.5525904]]

运行图片：

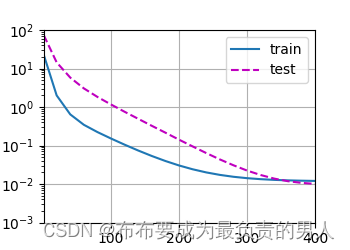
线性函数拟合（欠拟合）

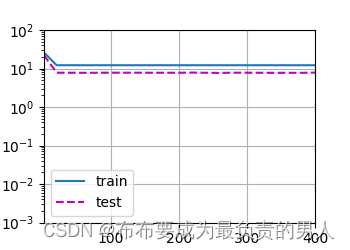
如果我们用线性函数，也就是只需要多项式特征中选择前两个维度（x⁰和x¹），此时减少改模型的训练损失就比较困难了。最后一个迭代周期完成以后，训练损失仍然很高，如此可以看出模型太简单容易造成欠拟合。

# 从多项式特征中选择前2个维度，即1和x
train(poly_features[:n_train, :2], poly_features[n_train:, :2],labels[:n_train], labels[n_train:])
d2l.plt.show()

输出：

weight: [[3.0301607 4.413203 ]]

图片：

高阶多项式函数拟合（过拟合）

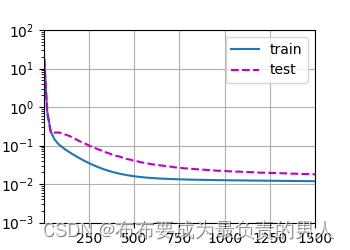
此时，如果我们在多项式特征中选取了所有的维度，但是此时我们没有足够的数据用于学到高阶系数应该具有接近于0的值。因此，这个复杂的模型就会很容易受到训练数据中的噪声的影响了。虽然训练损失可以有效降低，但测试损失仍然很高。结果表明，复杂模型对数据造成了过拟合。

# 从多项式特征中选取所有维度
train(poly_features[:n_train, :], poly_features[n_train:, :],labels[:n_train], labels[n_train:], num_epochs=1500)
d2l.plt.show()

输出结果：

weight: [[ 5.0168414 1.3087198 -3.4513204 5.1666236 0.10954458 1.1009666
0.18435563 0.17159764 0.15245272 0.12382802 -0.13876013 -0.14683287
-0.18860853 -0.19347051 0.10141594 0.09009624 -0.02940431 0.18723282
-0.20842025 0.04670855]]

图片：