SAD notes

ESKF 总结

prediction

更新误差先验
在这里插入图片描述

$F$ 通过3.42来算
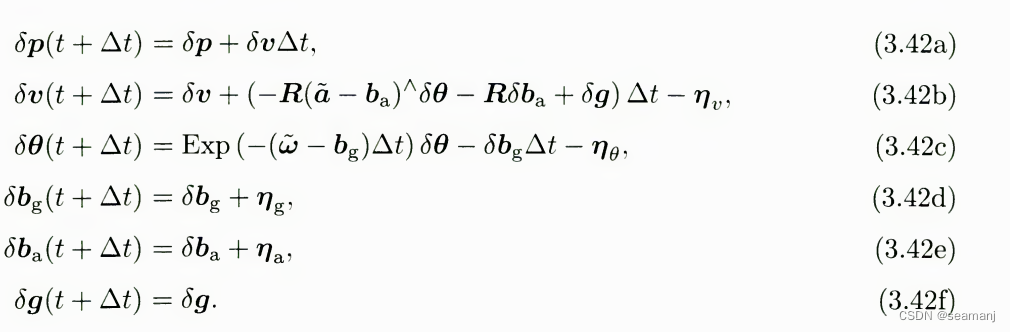
在这里插入图片描述
得到

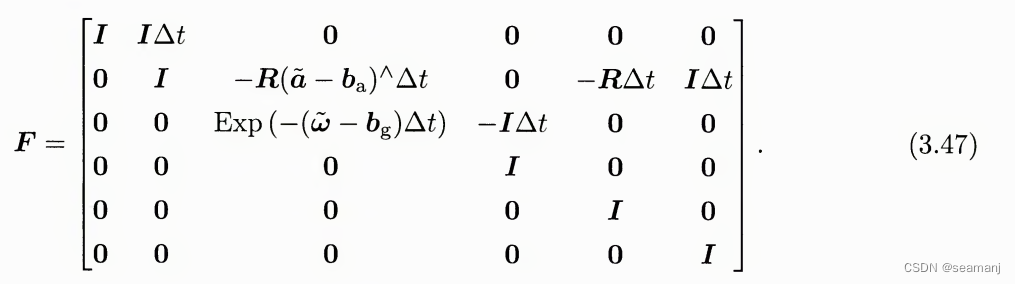
这里有点绕的一点是: 误差状态的 $F$ 牵涉到名义状态, 而名义状态又需要在时间上推进更新

其中, F中的名义状态的推进通过公式3.41得到,

(名义状态不考虑误差, 这一点从3.41d, 3.41e可以看出, 误差状态只考虑误差, 真实状态为名义+误差)

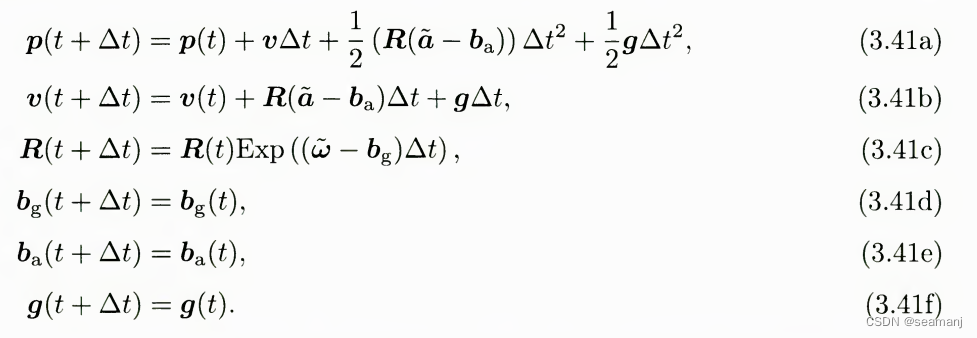在这里插入图片描述代码的实现

template <typename S>
bool ESKF<S>::Predict(const IMU& imu) {assert(imu.timestamp_ >= current_time_);double dt = imu.timestamp_ - current_time_;if (dt > (5 * options_.imu_dt_) || dt < 0) {// 时间间隔不对，可能是第一个IMU数据，没有历史信息LOG(INFO) << "skip this imu because dt_ = " << dt;current_time_ = imu.timestamp_;return false;}// nominal state 递推VecT new_p = p_ + v_ * dt + 0.5 * (R_ * (imu.acce_ - ba_)) * dt * dt + 0.5 * g_ * dt * dt;VecT new_v = v_ + R_ * (imu.acce_ - ba_) * dt + g_ * dt;SO3 new_R = R_ * SO3::exp((imu.gyro_ - bg_) * dt);R_ = new_R;v_ = new_v;p_ = new_p;// 其余状态维度不变// error state 递推// 计算运动过程雅可比矩阵 F，见(3.47)// F实际上是稀疏矩阵，也可以不用矩阵形式进行相乘而是写成散装形式，这里为了教学方便，使用矩阵形式Mat18T F = Mat18T::Identity();                                                 // 主对角线F.template block<3, 3>(0, 3) = Mat3T::Identity() * dt;                         // p 对 vF.template block<3, 3>(3, 6) = -R_.matrix() * SO3::hat(imu.acce_ - ba_) * dt;  // v对thetaF.template block<3, 3>(3, 12) = -R_.matrix() * dt;                             // v 对 baF.template block<3, 3>(3, 15) = Mat3T::Identity() * dt;                        // v 对 gF.template block<3, 3>(6, 6) = SO3::exp(-(imu.gyro_ - bg_) * dt).matrix();     // theta 对 thetaF.template block<3, 3>(6, 9) = -Mat3T::Identity() * dt;                        // theta 对 bg// mean and cov predictiondx_ = F * dx_;  // 这行其实没必要算，dx_在重置之后应该为零，因此这步可以跳过，但F需要参与Cov部分计算，所以保留cov_ = F * cov_.eval() * F.transpose() + Q_; current_time_ = imu.timestamp_;return true;
}

$Q$ 的算法

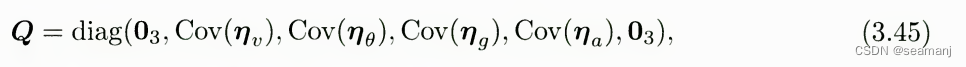
注意, 在离散情况下
$\begin{aligned} &\eta_v = \eta_a \Delta t\\ &\eta_ \theta = \eta_g \Delta t \\ &\eta_g = \eta_{bg} \Delta t\\ &\eta_ a = \eta_{ba} \Delta t \\ \end{aligned}$
可以根据3.40将3.42进行一阶泰勒展开
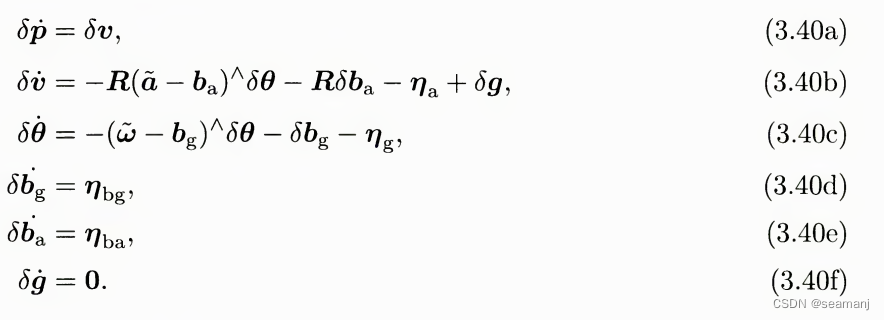
在这里插入图片描述

代码中的实现

        double ev = options.acce_var_;double et = options.gyro_var_;double eg = options.bias_gyro_var_;double ea = options.bias_acce_var_;double ev2 = ev;  // * ev;   // tj : 为什么没平方? Q里面应该是方差double et2 = et;  // * et;double eg2 = eg;  // * eg;double ea2 = ea;  // * ea;// 设置过程噪声Q_.diagonal() << 0, 0, 0, ev2, ev2, ev2, et2, et2, et2, eg2, eg2, eg2, ea2, ea2, ea2, 0, 0, 0;

其中options的定义

    struct Options {Options() = default;/// IMU 测量与零偏参数double imu_dt_ = 0.01;  // IMU测量间隔// NOTE IMU噪声项都为离散时间，不需要再乘dt，可以由初始化器指定IMU噪声double gyro_var_ = 1e-5;       // 陀螺测量标准差double acce_var_ = 1e-2;       // 加计测量标准差double bias_gyro_var_ = 1e-6;  // 陀螺零偏游走标准差double bias_acce_var_ = 1e-4;  // 加计零偏游走标准差

correction

更新误差后验

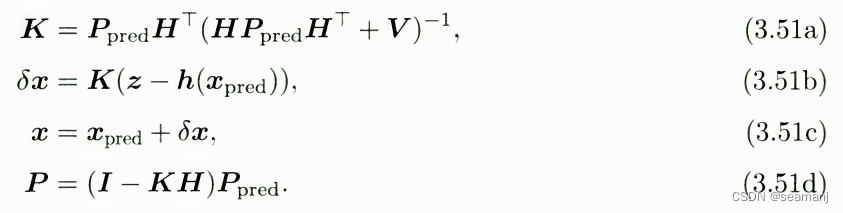
在这里插入图片描述

$H$ 是观测值对误差状态变量的jacob

先看GNSS, 它观测值有位移和旋转, 根据3.66和3.70可得 $H$ ,
在这里插入图片描述

GNSS对旋转的观测是总体的旋转, 然而名义上的 $R$ 是知道的, 所以我们可以将观测值变以成对于旋转误差状态的直接观测, 这样一来, 它对自己求导就为 $I$

同理, GNSS对位移的观测是总体的位移, 然后名义上的 $p$ 是知道, 所以我们将对总体位移的观测转到对于误差位移的直接观测

    Eigen::Matrix<S, 6, 18> H = Eigen::Matrix<S, 6, 18>::Zero();H.template block<3, 3>(0, 0) = Mat3T::Identity();  // P部分 (3.70)H.template block<3, 3>(3, 6) = Mat3T::Identity();  // R部分（3.66)

然后求 $V$

 // 卡尔曼增益和更新过程Vec6d noise_vec;noise_vec << trans_noise, trans_noise, trans_noise, ang_noise, ang_noise, ang_noise;Mat6d V = noise_vec.asDiagonal();

其中trans_noise, ang_noise在option中定义

        /// RTK 观测参数double gnss_pos_noise_ = 0.1;                   // GNSS位置噪声double gnss_height_noise_ = 0.1;                // GNSS高度噪声double gnss_ang_noise_ = 1.0 * math::kDEG2RAD;  // GNSS旋转噪声

然后更新后验3.51b, 3.51d

    // 更新x和covVec6d innov = Vec6d::Zero();innov.template head<3>() = (pose.translation() - p_);          // 平移部分innov.template tail<3>() = (R_.inverse() * pose.so3()).log();  // 旋转部分(3.67)dx_ = K * innov;cov_ = (Mat18T::Identity() - K * H) * cov_;

有了误差状态, 就可以更新名义状态3.51c

   /// 更新名义状态变量，重置error statevoid UpdateAndReset() {p_ += dx_.template block<3, 1>(0, 0);v_ += dx_.template block<3, 1>(3, 0);R_ = R_ * SO3::exp(dx_.template block<3, 1>(6, 0));if (options_.update_bias_gyro_) {bg_ += dx_.template block<3, 1>(9, 0);}if (options_.update_bias_acce_) {ba_ += dx_.template block<3, 1>(12, 0);}g_ += dx_.template block<3, 1>(15, 0);ProjectCov();dx_.setZero();}

注意这里有一步需要投影, 参考3.63

在这里插入图片描述

/// 对P阵进行投影，参考式(3.63)
void ProjectCov() {Mat18T J = Mat18T::Identity();J.template block<3, 3>(6, 6) = Mat3T::Identity() - 0.5 * SO3::hat(dx_.template block<3, 1>(6, 0));cov_ = J * cov_ * J.transpose();
}

再看odom, 它观测值只有速度

首先求H, 注意这里观测值为本地速度, 但是名义变量 $R$ 这时是知道的, 所以可以把观测值从本地速度转化到世界速度, 然后世界速度对世界速度求导就为 $I$

在这里插入图片描述

// odom 修正以及雅可比
// 使用三维的轮速观测，H为3x18，大部分为零
Eigen::Matrix<S, 3, 18> H = Eigen::Matrix<S, 3, 18>::Zero();
H.template block<3, 3>(0, 3) = Mat3T::Identity();

然后算V

// 设置里程计噪声
double o2 = options_.odom_var_ * options_.odom_var_;
odom_noise_.diagonal() << o2, o2, o2;

option里面的定义

/// 里程计参数
double odom_var_ = 0.5;
double odom_span_ = 0.1;        // 里程计测量间隔
double wheel_radius_ = 0.155;   // 轮子半径
double circle_pulse_ = 1024.0;  // 编码器每圈脉冲数

然后更新后验

本地速度观测值的算法参见 3.76

// velocity obs
double velo_l = options_.wheel_radius_ * odom.left_pulse_ / options_.circle_pulse_ * 2 * M_PI / options_.odom_span_;
double velo_r =options_.wheel_radius_ * odom.right_pulse_ / options_.circle_pulse_ * 2 * M_PI / options_.odom_span_;
double average_vel = 0.5 * (velo_l + velo_r);VecT vel_odom(average_vel, 0.0, 0.0);
VecT vel_world = R_ * vel_odom;dx_ = K * (vel_world - v_);// update cov
cov_ = (Mat18T::Identity() - K * H) * cov_;
UpdateAndReset();