2016年亚太杯APMCM数学建模大赛A题基于光学信息数据的温度及关键元素含量预测求解全过程文档及程序

2016年亚太杯APMCM数学建模大赛

A题基于光学信息数据的温度及关键元素含量预测

原题再现

光含有能量，在一定条件下可以转化为热。燃烧是一种常见的现象，既能发光又能发热。光和热通常是同时存在的，一般来说，光强度越高，温度越高。
光强度与温度没有直接关系，但光频率与温度有很大关系，如低频红外光和远红外光，具有典型的热效应，而高频紫外光几乎没有热效应。在相同频率下，光强越大，热效应越好。
金属熔炼是将金属材料抛入一定的熔炉中，在一定温度下进行熔炼，以控制或消除劣质元素，保持或增加劣质元素的比例。从而寻求获得目标金属的最佳性能。因此，金属冶炼的关键在于温度和关键元素含量的控制。在金属冶炼过程中，炉膛产生火焰，通过小孔成像原理将火焰发出的光学信息投影到光电探测器上。然后，根据离散频率，由光电探测器每隔0.5s记录一次火焰的光强数据。某一时刻光信息数据生成过程：
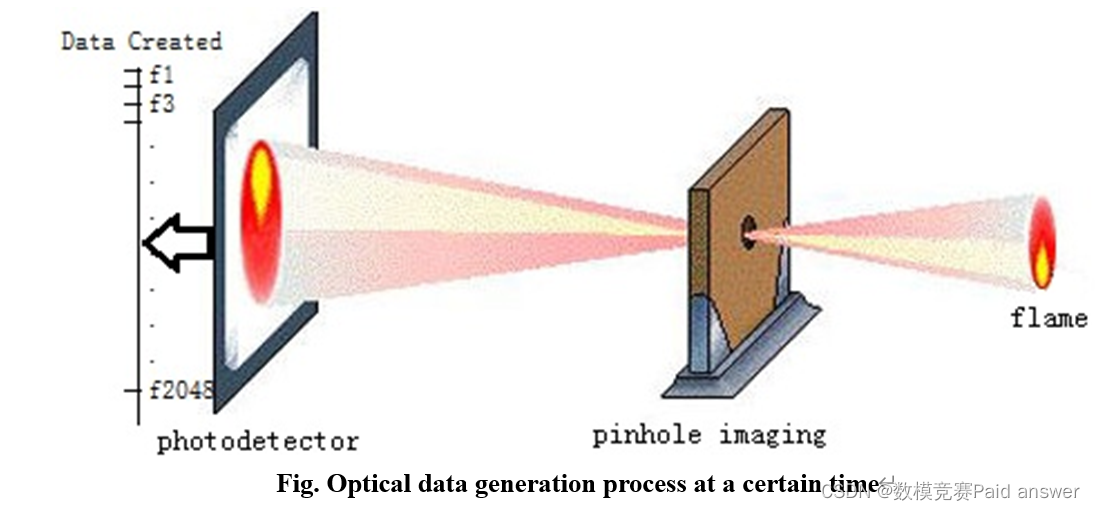
在这里插入图片描述
从上面的图像中，光电探测器每0.5秒接收的数据量为2048。需要利用2048光强值实时预测火焰温度和原料中关键元素的含量。

附录给出了1.xlsx、2.xlsx和3.xlsx三种金属熔炼过程的数据，包括时间t、燃烧气体累积消耗量Q、燃烧气体累积消耗率p、光学信息数据（f\u 1-f\u 2048，不同频率的光强）、开尔文温度t和关键元素C的含量。

词汇表：
光学信息特性：以一次生成的2048光强数据为输入，以火焰温度和关键元素含量为输出，建立数学模型必然比较复杂，无法达到预测结果。为了减少输入数据的数量，尝试寻找一个或多个光强数据的特征值，将其作为输入，降低模型计算的复杂度，增强模型的适用性。
交叉实验：给出了三种金属冶炼过程的数据，建立了基于三种不同工艺的温度和关键元素含量预测模型。为了验证该模型的通用性，分别对1过程和2过程、3过程进行了仿真。然后探讨了误差特性。交叉试验设计见下表：
在这里插入图片描述
Err11表示基于1工序预测模型的自检误差，Err21表示基于1工序预测模型和2工序数据的交叉检验误差，依此类推。
通过以上背景，探索以下三个问题：

1）根据附件中给出的数据建立数学模型或算法模型，求出光学信息数据的特征λ，并将特征（λ1，λ2，…，λn）提取到Excel表格中。数据文件名为：feature\u output\u 1.xlsx、feature\u output\u 2.xlsx和feature\u output\u 3.xlsx。
2）利用1）中提取的光学信息特征数据和数据表中给出的时间t、助燃气体累计消耗量Q等数据，建立数学模型或算法模型，预测开尔文温度t和关键元素含量C，并探讨其关系。
3）通过问题1）和问题2）的探索，设计交叉实验方案，交叉验证预测目标产生的误差，并在误差分析的基础上给出误差控制方案。

整体求解过程概述(摘要)

在金属冶炼过程中，温度和关键元素含量的控制对获得目标金属的最佳性能具有重要意义。本文的核心目标是建立一个数学模型或算法模型，来描述在燃气比累积消耗量和燃气累积消耗率条件下，温度、关键元素含量与光照强度之间的关系。
在第一个问题中，我们采用主成分分析法，从每0.5秒记录的2048组光强数据中找出特征值。根据SPSS软件计算的原始光强数据的计算结果，可以用13个主成分来表示2048组数据的光学信息。以各主成分的贡献率为权重，通过加权求和得到特征值，可以代表原始光强数据的绝大部分信息。
在第二个问题中，我们首先探讨了光学信息特征数据λ的规律，发现它可以很好地拟合成线性函数。特别地，由于λ的散点图的特殊性，我们在过程1中采用了分割函数。然后通过观察和探索，决定采用多元线性回归预测开尔文温度和关键元素含量C，最后进行相关检验，检验结果是否显著，并得到正确答案。从而得出多元线性回归可以预测T和C的结论，并给出了各过程的预测表达式。
在第三个问题中，我们首先在三个预测模型和三个过程数据之间进行交叉实验，计算交叉实验中每个单元的均方误差。并对模型的普适性进行了一般性分析。然后，为了提高模型的通用性和控制误差，对整个过程中的误差来源进行了全面详细的分析。区分了误差中可人为控制的部分。针对不同类型的误差，从给定数据的误差、PCA算法的误差、回归预测模型的误差和随机误差四个方面提出了提高模型精度和通用性的误差控制方案。

模型假设：

1.假设所选主成分具有高度代表性。
2.假设代表85%以上信息的特征值可以代替所有原始光强数据。
3.假设原始光强数据之间有很强的相关性
4.附录1-3中给出的数据真实有效。
5.由问题1得到的光学信息特征数据λ是正确的。
6.光学信息特征数据λ可以在可接受的范围内波动，少数离群数据可以丢弃。。
7.没有更多的元素会影响开尔文温度T和关键元素含量C的预测。

问题分析：

问题1分析
给出了从金属冶炼过程中提取的三组数据，包括时间t、燃烧气体累积消耗量Q、燃烧气体累积消耗率p、光学信息数据（f\u 1-f\u 2048，不同频率的光强）、开尔文温度t和关键元素C的含量。如果以一次生成的2048个光强数据为输入，以火焰温度和关键元素含量为输出，构建数学模型必然比较复杂，因此我们的核心任务是找到一个或多个光强数据的特征值来代表原始数据中的大部分信息。采用主成分分析的方法对2048组数据进行降维处理，将原始数据替换为维数较小且互不相关的主成分。利用SPSS软件计算了光强数据的特征值。

问题2分析
问题2要求我们利用光学信息特征数据λ、时间t和累积消耗量Q来预测开尔文温度t和关键元素含量C。通过观察，我们发现变量t、Q、t和C呈线性增加，变量λ的散点图表明它可以拟合成一条直线。因此，我们决定选择多元线性回归预测开尔文温度T和关键元素含量C。

问题3分析
问题3首先设计一个交叉实验，并根据交叉实验结果交叉验证预测目标产生的误差。进一步根据分析结论设计误差控制方案。在我们的研究中，误差的构成可能包括但不限于问题求解的模型和算法以及随机误差。在分析误差来源的基础上，提出一种误差控制方法。所以，我们将测试误差分为可控制和不可人工功率两类。，并提出了不同的误差控制方法。从而达到提高模型通用性的目的。

模型的建立与求解整体论文缩略图

在这里插入图片描述

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

部分程序如下:

%T 总程序
%T1 总程序
clear;clc
load APMCM1
y1=polyfit(time1,lamda1,1); %对散点图进行线性拟合
lamdatest1=y1(1)*time1+y1(2);
figure (1)
x1=1:269;
plot(x1,lamda1,'b-');
hold on
plot(x1,lamdatest1,'r-');
title('lamda 拟合');
xlabel('t');
ylabel('lamda');
legend('实验值','预测值');
%对 T1 进行多元回归
e1=ones(269,1);
X1=[e1,time1,Q1,lamdatest1];
[b1,bint1,r1,rint1,stats1]=regress(T1,X1,0.05);
figure (2)
rcoplot(r1,rint1);
%绘制 T1 与 Ttest1 曲线
Ttest1=b1(1)+b1(2)*time1+b1(3)*Q1+b1(4)*lamdatest1;
figure (3)
x1=1:269;
subplot(1,2,1)
plot(x1,T1,'b-');
title('温度 T 的多元回归');
xlabel('横坐标');
ylabel('T');
legend('实验值');
subplot(1,2,2)
plot(x1,Ttest1,'r-');
xlabel('横坐标');
ylabel('T');
legend('预测值');
figure (4)
plot(x1,T1,'b-');
hold on
plot(x1,Ttest1,'r-');
title('温度 T 的多元回归');
xlabel('横坐标');
ylabel('T');
legend('实验值','预测值');
%T2 总程序
y2=polyfit(time2,lamda2,1);% 对散点图进行线性拟合
lamdatest2=y2(1)*time2+y2(2);
%lamdatest2=[];
%for i=1:135
% lamdatest2(i,1)=1.9.*time2(i)+1276.9;
%end
figure (5)
x2=1:135;
plot(x2,lamda2,'b-');
hold on
plot(x2,lamdatest2,'r-');
title('lamda 拟合');
xlabel('t');
ylabel('lamda');
legend('实验值','预测值');
%用 SPSS 对 lamda 和 lamdatest 进行相关性检测
%对 T2 进行多元回归
e2=ones(135,1);
X2=[e2,time2,Q2,lamdatest2];
[b2,bint2,r2,rint2,stats2]=regress(T2,X2,0.05);
figure (6)
rcoplot(r2,rint2)
%绘制 T2 与 Ttest2 曲线
Ttest2=b2(1)+b2(2)*time2+b2(3)*Q2+b2(4)*lamdatest2;
%Ttest2=[];
%for i=1:135
% Ttest2(i)=-1.9956.*time2(i)+0.1605.*Q2(i)+1.0503.*lamdatest2(i);
%end
figure (7)
x2=1:135;
subplot(1,2,1)
plot(x2,T2,'b-');
title('温度 T 的多元回归');
xlabel('横坐标');
ylabel('T');
legend('实验值');
subplot(1,2,2)
plot(x2,Ttest2,'r-');
xlabel('横坐标');
ylabel('T');
legend('预测值');
figure (8)
plot(x2,T2,'b-');
hold on
plot(x2,Ttest2,'r-');
title('温度 T 的多元回归');
xlabel('横坐标');
ylabel('T');
legend('实验值','预测值');
%绘制 T 与 Ttest 曲线
Ttest=[];
for i=1:404
if i<=269Ttest(i)=Ttest1(i);
elseTtest(i)=Ttest2(i-269);
end
end
figure (9)
x=1:404;
plot(x,T,'b-','linewidth',2)
hold on
plot(x,Ttest,'r-','linewidth',2)
title('mutiple linear regression for T prediction');
xlabel('xlabel');
ylabel('T');
h1=legend('actual value','fitted value');
set(h1,'Fontsize',14)
figure (10)
subplot(1,2,1)
plot(x,T,'b-','linewidth',2)
title('mutiple linear regression for T prediction');
xlabel('xlabel');
ylabel('T');
h2=legend('actual value');
subplot(1,2,2)
plot(x,Ttest,'r-','linewidth',2)
xlabel('xlabel');
ylabel('T');
h3=legend('fitted value');
set(h2,'Fontsize',14);
set(h3,'Fontsize',14);

%探索 T、C 之间的关系
clear;
clc;
load APMCM1;
%C 和 T 的线性回归
e=ones(404,1);
X=[e,T];
[b,bint,r,rint,stats]=regress(C,X,0.05);
figure (1)
rcoplot(r,rint)
Ctest=b(1)+b(2)*T;
%y3=polyfit(T,C,1);
%Ctest=y3(1)*T+y3(2);
ttt=1:404;
figure (2)
plot(ttt,C,'b-','linewidth',2)
hold on
plot(ttt,Ctest,'r-','linewidth',2)
title('The relationship between T and C')
xlabel('T');
ylabel('C');
h=legend('actual value','fitted value');
set(h,'Fontsize',14)
b
%y3 %线性拟合参数 常数项 α