39.B树，B+树（王道第7章查找补充知识）

一. B树

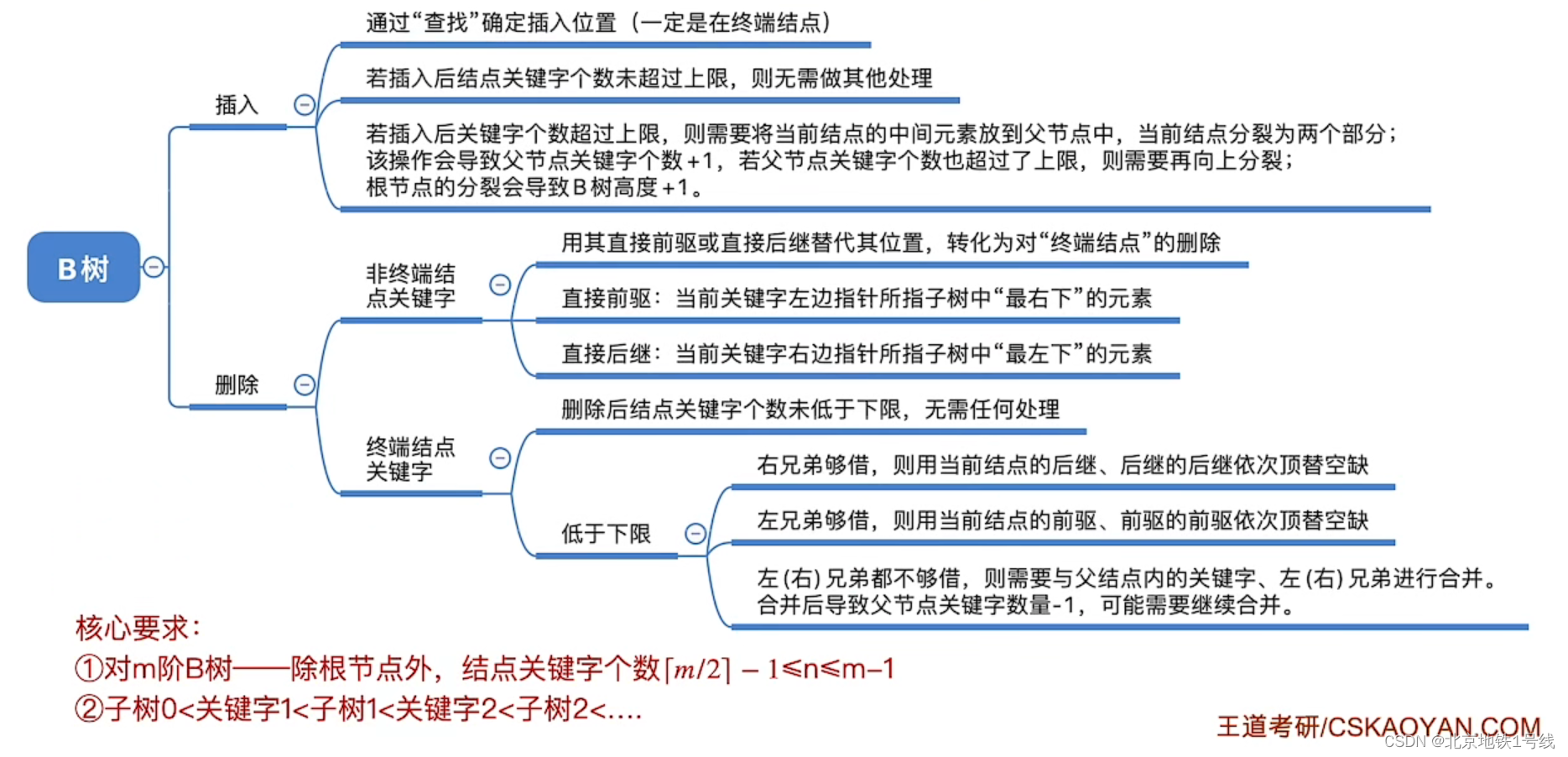
（1）B树的定义

（2）B树的高度

（3）B树的插入

（4）B树的删除

二. B+树

（1）B+树的定义

（2）B+树与B树的区别

一. B树

（1）B树的定义

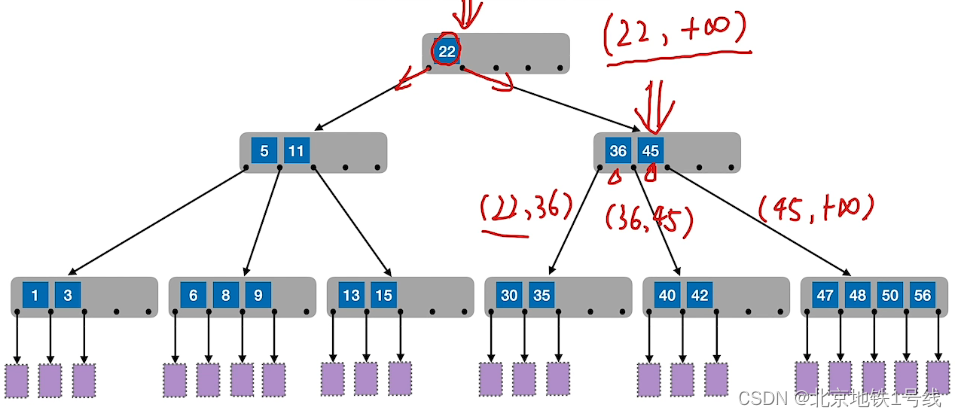
我们首先从二叉查找树到m叉查找树：如下是一个5叉查找树，这里每个结点最多可以有4个关键字，一个关键字可以把区间分成两个部分。

为了保证查找效率，防止树过高的策略：

（1）m叉查找树中，规定除了根节点外，任何结点至少有 $\left \lceil m/2 \right \rceil$ 个分叉，即至少含有 $\left \lceil m/2 \right \rceil-1$ 个关键字。如对于5叉排序树，每个结点至少要有3个分叉，2个关键字。

（2）仿照平衡二叉树：在m叉查找树中，规定对于任何一个结点，其所有子树的高度都要相同。

对于以上的m叉树，就称为m阶B树，下面给出B树的定义：

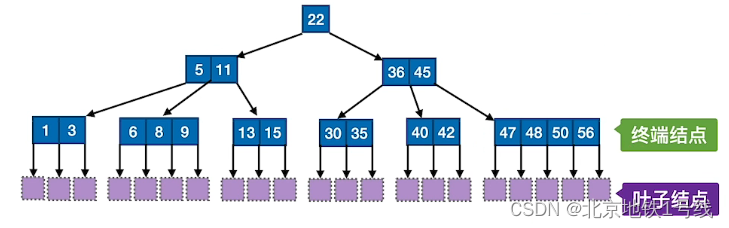
B树，又称多路平衡查找树，B树中所有结点的孩子个数的最大值称为B树的阶，通常用m表示。一棵m阶B树或为空树，或为满足如下特性的m叉树：

1）树中每个结点至多有m棵子树，即至多含有m-1个关键字。
2）若根结点不是终端结点，则至少有两棵子树。
3）除根结点外的所有非叶结点至少有 $\left \lceil m/2 \right \rceil$ 棵子树，即至少含有 $\left \lceil m/2 \right \rceil-1$ 个关键字。
4）所有非叶子结点的结构如下：
$n$ $P_0$ $K_1$ $P_1$ $K_2$ $P_2$ ... $K_n$ $P_n$
其中，Ki (i= 1,2.., n)为结点的关键字，且满足K1<K2<...<Kn；Pi (i = 0,1..., n)为指向子树根结点的指针，且指针Pi-1所指子树中所有结点的关键字均小于Ki，Pi所指子树中所有结点的关键字均大于Ki，n（ $\left \lceil m/2 \right \rceil-1\leq n\leq m-1$ ）为结点中关键字的个数。
5）所有的叶结点（失败结点）都出现在同一层次上，并且不带信息(可以视为外部结点或类似于折半查找判定树的查找失败结点，实际上这些结点不存在，指向这些结点的指针为空)。

（2）B树的高度

下面讨论B树的高度：对于一个包含n个关键字，高度为h，阶数为m的B树（需要说明的是高度一般不包含叶子结点/失败结点）：

最小高度：尽可能填满。第一层1个结点，每个结点有m-1个关键字；第二层m个结点，每个结点有m-1个关键字；第三层 $m^2$ 个结点，每个结点有m-1个关键字；所以有 $n\leq (m-1)(1+m+m^2+...+m^{h-1})=m^h-1$ ，因此 $h\geq log_m(n+1)$ ；

最大高度：尽可能空置。第一层1个结点，第二层2个结点，第三层有 $2\left \lceil m/2 \right \rceil$ 个结点，第h层有 $2\left \lceil m/2 \right \rceil^{h-2}$ 个结点，叶子结点最少有 $2\left \lceil m/2 \right \rceil^{h-1}$ 个，由于叶子结点就是n+1个（n个关键字分成n+1段区间），所以 $2\left \lceil m/2 \right \rceil^{h-1}\leq n+1$ ，也就是 $h\leq log_{\left \lceil m/2 \right \rceil}((n+1)/2)+1$ ；

（3）B树的插入

核心要求：

（1）对m阶B树——除根节点外，结点关键字个数 $\left \lceil m/2 \right \rceil-1\leq n\leq m-1$

（2）子树0<关键字1<子树1<关键字2<子树2<....

（3）新元素一定是插入到最底层“终端节点”，用“查找”来确定插入位置（否则失败结点将不在同一层）。

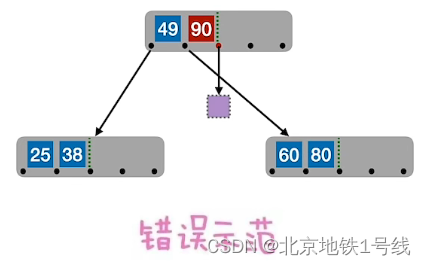
在插入key后，若导致原结点关键字数超过上限，则从中间位置（ $\left \lceil m/2 \right \rceil$ ）将其中的关键字分为两部分，左部分包含的关键字放在原结点中，右部分包含的关键字放到新结点中，中间位置 $\left \lceil m/2 \right \rceil$ 的结点插入原结点的父结点。若此时导致其父结点的关键字个数也超过了上限，则继续进行这种分裂操作，直至这个过程传到根结点为止，进而导致B树高度增1.

例：对于一个5阶B树，结点关键字个数是 $\left \lceil m/2 \right \rceil-1\leq n\leq m-1$ ，也就是 $2\leqslant n\leqslant 4$ ，现插入25，38，49，60，80，90，99，88，83，87，70，92，93，94，73，74，75

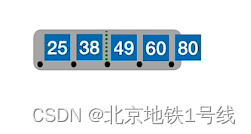
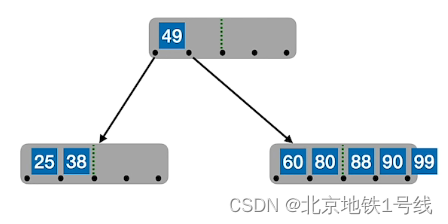
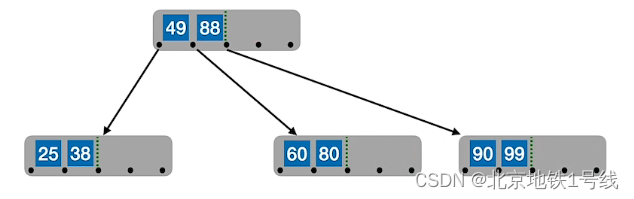
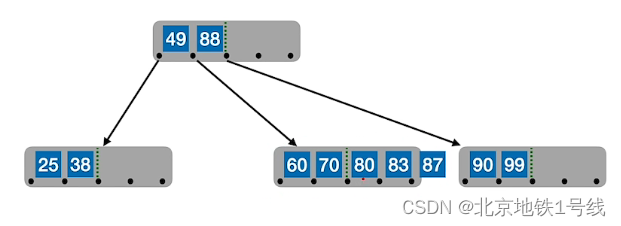
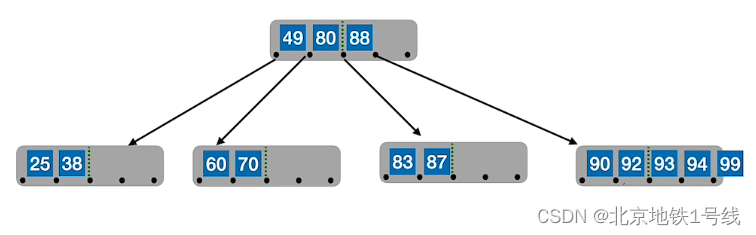
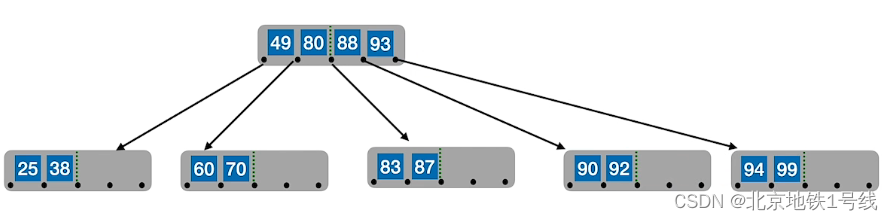
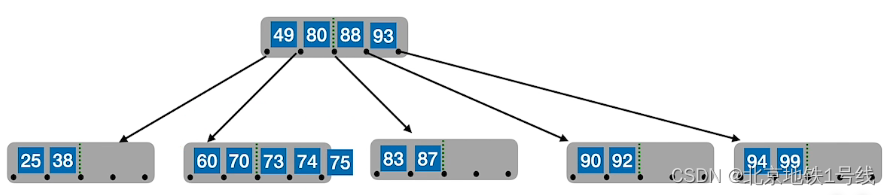
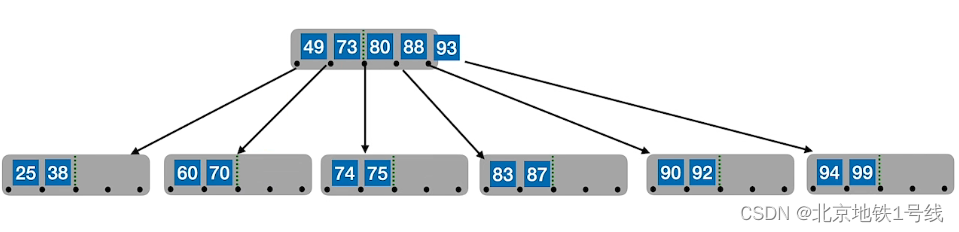
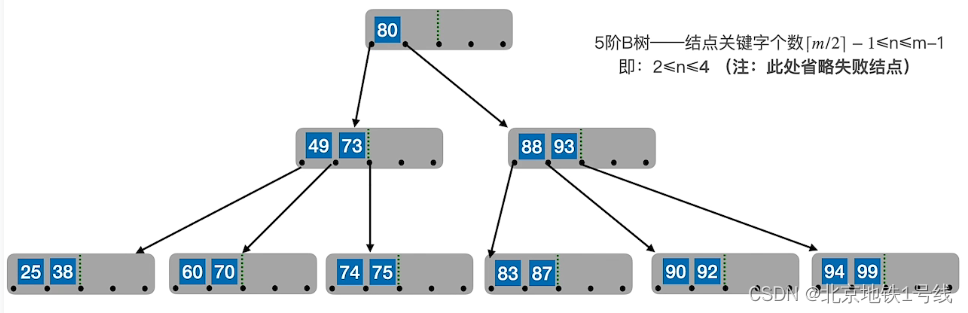
（4）B树的删除

（1）若被删除关键字在终端节点，则直接删除该关键字（要注意节点关键字个数是否低于下限 $\left \lceil m/2 \right \rceil-1$ )

如在上面的B树里删除60：

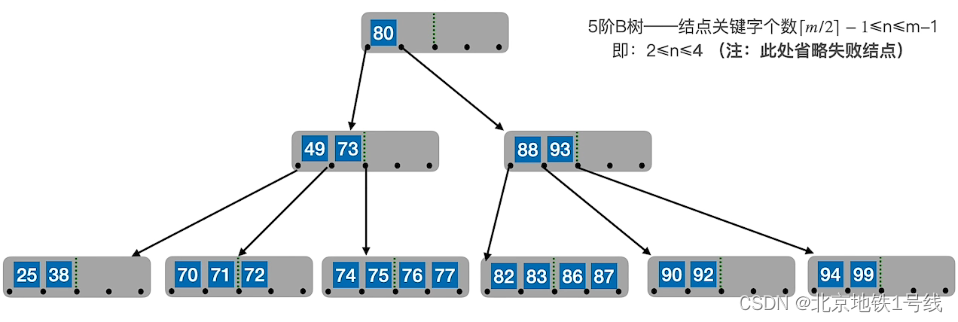
（2）若被删除关键字在非终端节点，则用直接前驱或直接后继来替代被删除的关键字。对非终端结点关键字的删除,必然可以转化为对终端结点的删除操作。
直接前驱：当前关键字左侧指针所指子树中“最右下”的元素；直接后继：当前关键字左侧指针所指子树中“最左下”的元素；

直接前驱/直接后继一定是终端结点！

如在（1）的基础上删除80，找直接前驱77替代：

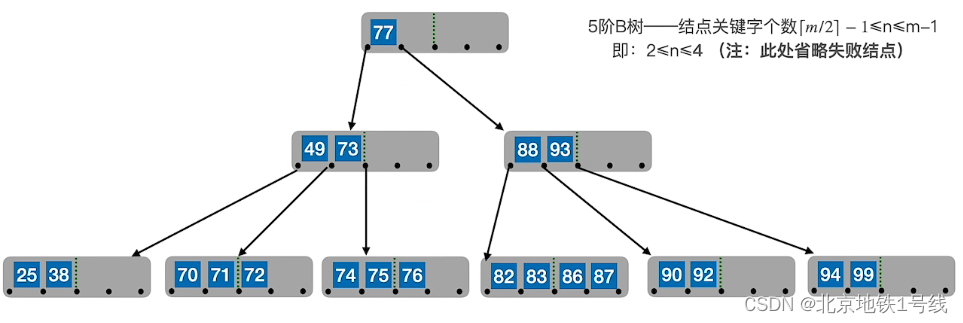
然后再删除77，用后继82替代：

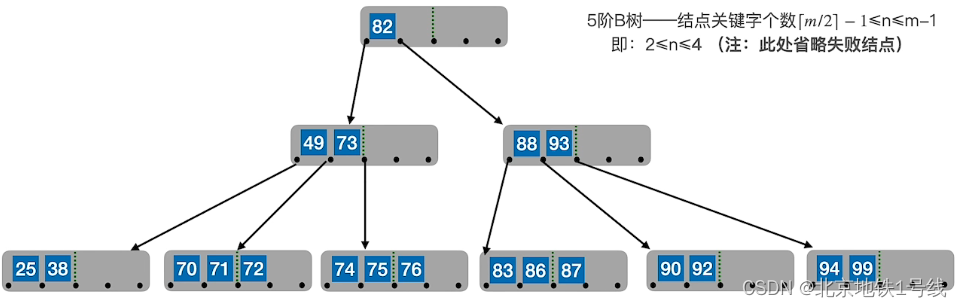
（3）如果删除叶子结点导致结点关键字个数低于下限，且与此结点右(或左)兄弟结点的关键字个数还很宽裕，则需要调整该结点、右（或左）兄弟结点及其双亲结点（父子换位法）
说白了，当右兄弟很宽裕时，用当前结点的后继、后继的后继来填补空缺。

例如删除38，借用右面的兄弟结点中的70：

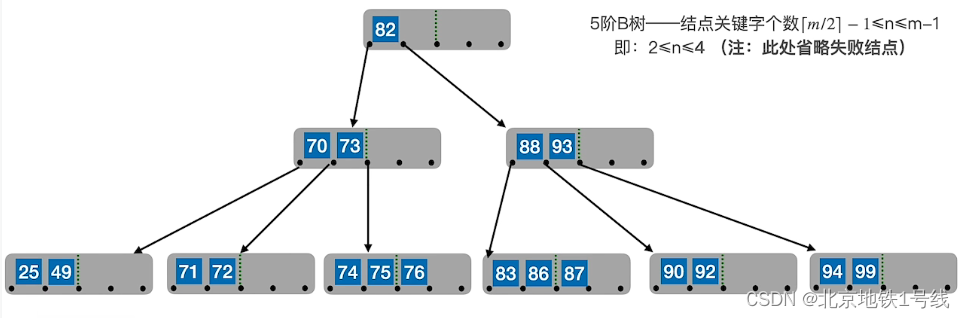
再删除90，借用左面的兄弟结点中的87：

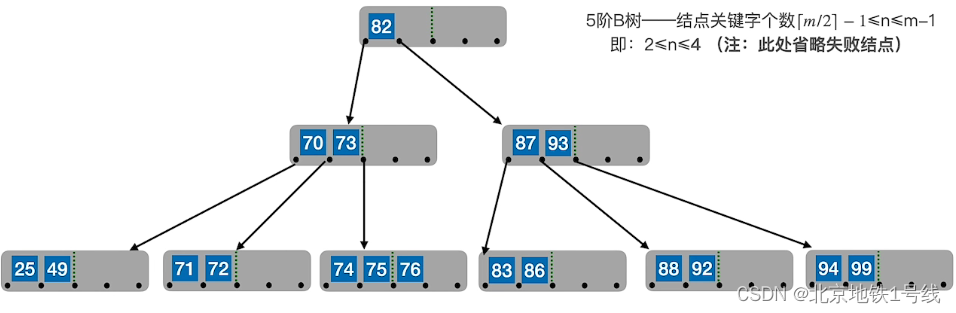
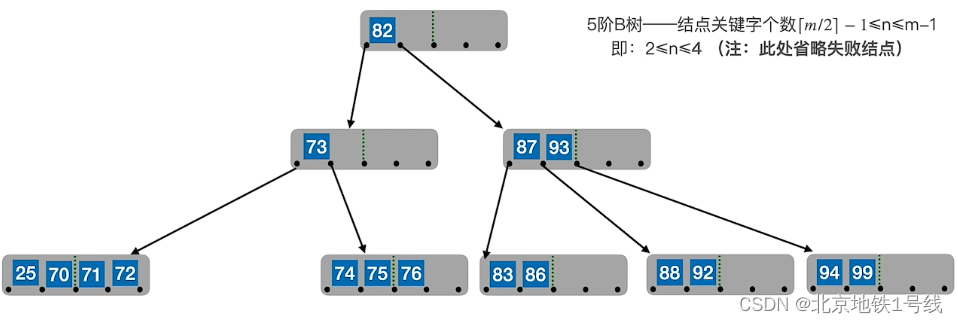
（4）若被删除关键字所在结点删除前的关键字个数低于下限，且此时与该结点相邻的左、右兄弟结点的关键字个数均为 $\left \lceil m/2 \right \rceil-1$ ，则将关键字删除后与左(或右)兄弟结点及双亲结点中的关键字进行合并。

例如：继续删除49：

二. B+树

（1）B+树的定义

一棵m阶的B+树需满足下列条件：

每个分支结点最多有m棵子树(孩子结点)。
非叶根结点至少有两棵子树，其他每个分支结点至少有 $\left \lceil m/2 \right \rceil$ 棵子树。
结点的子树个数与关键字个数相等。
所有叶结点包含全部关键字及指向相应记录的指针，叶结点中将关键字按大小顺序排列，并且相邻叶结点按大小顺序相互链接起来（支持顺序查找）。
所有分支结点中仅包含它的各个子结点中关键字的最大值及指向其子结点的指针。

需要注意的是：对于多路查找，无论查找成功与否，最终都会走到叶子结点，这是和B树不一样的地方。

在B+树中，非叶结点不含有该关键字对应记录的存储地址。可以使一个磁盘块可以包含更多个关键字，使得B+树的阶更大，树高更矮，读磁盘次数更少，查找更快。

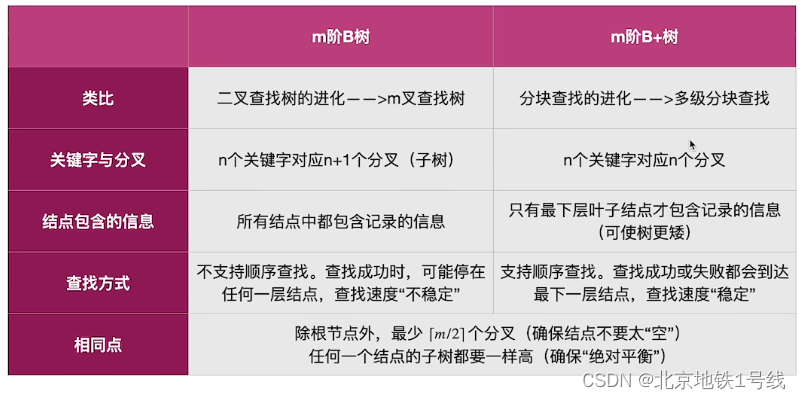
（2）B+树与B树的区别

对于m阶B+树与m阶B树：

1）B+树结点中的n个关键字对应n棵子树，B树结点中的n个关键字对应n+1棵子树

2）对m阶B+树，根结点关键字个数 $n\in \left [ 2,m \right ]$ ，其他结点关键字个数 $n\in \left [ \left \lceil m/2 \right \rceil,m \right ]$ 。对m阶B树，根结点关键字个数 $n\in \left [ 1,m-1 \right ]$ ，其他结点关键字个数 $n\in \left [ \left \lceil m/2 \right \rceil-1,m-1 \right ]$