论文地址：https://arxiv.org/pdf/2307.07635v1.pdf

官方地址：https://co-tracker.github.io/
github地址：https://github.com/facebookresearch/co-tracker/tree/main

引言

在计算机视觉领域，光流估计是历史最久远的问题之一，早期的方法尝试通过解决色彩恒定性引起的简单微分方程来处理。然而，随着深度学习技术的不断进步，现代光流问题已经迈入了一个全新的阶段。其中，《CoTracker: It is Better to Track Together》这篇令人瞩目的论文，为我们带来了一种高效且准确的光流估计器。在此之前，该论文精彩总结了光流估计的历史发展背景，涵盖了众多经典和现代光流算法。从最初的色彩恒定性方法，到FlowNet和FlowNet2等引领潮流的端到端卷积网络，再到更近期的Transformer和深度学习方法，该文对光流估计领域的技术进展进行了全面梳理。这一综述为读者们提供了深入了解光流估计研究历程的机会，同时也为CoTracker的出现奠定了坚实的理论基础。本博客将着重介绍CoTracker这篇杰出论文，展示它是如何在光流估计领域取得突破性进展，为长期跟踪问题提供了全新的解决方案。

光流估计发展

按时间顺序和技术复杂度列出光流估计的一些技术：

1. 色彩恒定性方法 [16, 24, 4, 5]：最初的光流估计方法，通过解决由色彩恒定性引起的简单微分方程来处理。
2. FlowNet [12]：第一个端到端的用于光流估计的卷积网络，由Dosovitskiy等人引入。
3. FlowNet2 [18]：在FlowNet的基础上，通过堆叠架构和图像配准进一步改进的光流估计方法。
4. DCFlow [46]：提出了构建4D成本体积的方法，该成本体积捕捉了源图像和目标图像特征之间的关系。
5. PWC-Net [39]：使用了DCFlow中的成本体积，并引入金字塔处理和图像配准以降低计算成本。
6. RAFT [41]：保留了高分辨率的光流并增量更新光流场，启发了后续的研究工作。
7. Flowformer [17]：从RAFT汲取灵感，提出了基于Transformer的方法，对4D成本体积进行了分词处理。
8. GMFlow [48]：将更新网络替换为具有自注意力的softmax以进行优化。
9. Perceiver IO [19]：提出了一个统一的Transformer框架，可应用于多个任务，包括光流估计。
10. Kalman滤波方法 [9, 13]：传统的多帧光流方法，用于确保时间一致性。
11. VideoFlow [33]：将光流扩展到三个和五个连续帧，通过在光流优化期间集成前向和后向运动特征。
12. TAP-Vid [10]：提出了在视频中跟踪任何物理点的问题，并为其提供了基准测试和简单的基线方法。
13. Particle Video Revisited [15]：通过引入用于点遮挡跟踪的模型，重新审视了经典的Particle Video问题。
14. OmniMotion [44]：在测试时优化每个视频的体积表示，在规范空间中优化估计的对应关系。
15. MFT [27]：在远距离帧之间进行光流估计，并选择最可靠的光流链。
16. TAPIR [11]：一种前馈式点跟踪器，其匹配阶段受到TAP-Vid的启发，细化阶段受到PIPs的启发。

CoTracker跟踪器

目标和问题形式化

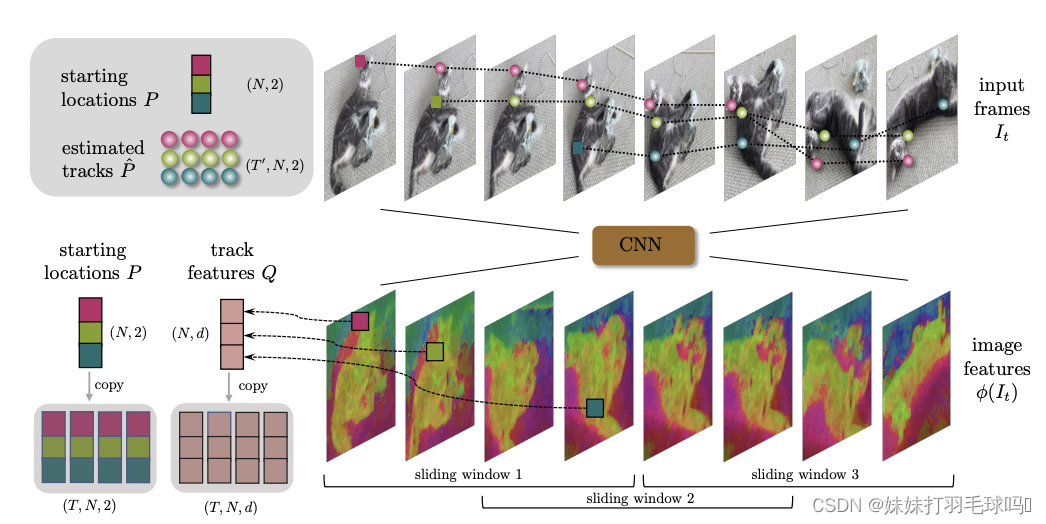
CoTracker的目标是在视频的持续时间内跟踪2D点。视频V由T个RGB帧组成，记作$V=(I_1,I_2,...,I_T)$。跟踪任务涉及为N个点生成轨迹$P_t^i=(x_t^i,y_t^i)\in R^2$，其中$t=t^i,...,T，i=1,...,N。t^i\in 1,...,T$表示轨迹开始的时间。另外，可见性标志 v t i ∈ { 0 , 1 } v^i_t ∈ \lbrace0, 1 \rbrace vti​∈{0,1}表示在给定帧中点是否可见或被遮挡。要求轨迹的起始点在初始时刻是可见的（即$v_{t^i}^i=1$）。注意，轨迹可以在视频的任何时间$1\le t^i\le T$开始。

CoTracker跟踪器的输入和输出

CoTracker算法以视频V和N个轨迹的起始位置和时间$(P_{t^i}^i,t^i{)}_i^N=1$作为输入，并输出所有有效时间 $(t\ge t_i)$的轨迹估计 $P_t^i=(x_t^i,y_t^i)$。跟踪器预测可见性标志的估计值 ${\hat{v}}_t^i$。在这些值中，只有初始值 ${\hat{P}}_{t^i}^i=P_{t^i}^i$和 ${\hat{v}}_{t^i}^i=v_{t^i}^i=1$是已知的，其他值需要进行预测。

CoTracker框架

CoTracker使用一个名为CoTracker的Transformer网络来预测轨迹的估计值。其大致结构如下：

$$\Psi ：G\mapsto O$$

在上面的式子中，轨迹使用输入tokens编码表示：$G_t^i$，其中$i=1,...,N$代表跟踪点，$t=1,...,T$代表时间。更新后的轨迹由相应的输出tokens表示：$O_t^i$。
具体地，CoTracker包含三个特征：

1. 图像特征

从每个视频帧$I_t$中提取d维外观特征$\varphi (I_t)\in R^{d\times \frac{H}{k}\times \frac{W}{k}}$，其中k = 8是一个下采样因子，用于提高效率。论文中考虑了多个缩放版本 $\varphi (I_t;s)\in R^{d\times \frac{H}{sk}\times \frac{W}{sk}}$，其中$s=1,...,S$。这些缩小的特征是通过对$s\times s$邻域内的基本特征应用平均池化得到的，其中$S=4$。

在项目中，选择提取外观特征的模型是用于图像分类任务的预训练模型 ResNet-18。ResNet（Residual Network）是一种深度卷积神经网络架构，通过使用残差块（Residual Blocks）解决了深度网络中梯度消失和梯度爆炸等问题，允许构建非常深的网络。

论文中提到的$\varphi (I_t)\in R^{d\times \frac{H}{k}\times \frac{W}{k}}$以及缩放版本$\varphi (I_t;s)\in R^{d\times \frac{H}{sk}\times \frac{W}{sk}}$是通过CNN对图像$I_t$进行处理得到的。

在代码中，外观特征的提取可以在get_appearance_features函数中找到，其代码如下：

def get_appearance_features(frames, model):"""Extracts appearance features for all frames using a given model.Args:frames: Tensor of shape (T, 3, H, W) representing T frames of the video.model: Pretrained CNN model used for feature extraction.Returns:Tensor of shape (T, d, H//k, W//k) representing the appearance features for each frame."""T, _, H, W = frames.size()frames = frames.reshape(T * 3, H, W)with torch.no_grad():features = model(frames.unsqueeze(1)).squeeze()return features.reshape(T, -1, H // k, W // k)

在这个函数中，frames是输入视频的帧序列，形状为(T, 3, H, W)，其中T表示帧数，3表示RGB通道，H和W分别表示帧的高度和宽度。model是一个预训练的CNN模型，用于特征提取。这里使用的CNN模型可能是在数据集上进行了预训练的，例如使用ImageNet数据集。

首先，对输入的帧序列进行一些形状变换，将其转换为形状为(T3, H, W)的张量。然后，将这个张量输入到CNN模型中，并通过model(frames.unsqueeze(1))得到输出特征张量。最后，通过squeeze()方法去除不需要的维度，得到形状为(Td, H//k, W//k)的特征张量。其中d表示特征的维度。

最后，通过reshape操作将特征张量重新恢复为形状为(T, d, H//k, W//k)的外观特征，它将被用于后续的跟踪过程。注意，这里提到的k和S的值分别对应于论文中提到的下采样因子和缩放版本的数量。

2. 跟踪特征

轨迹的特征由向量$Q_t^i\in R^d$表示，这些特征是与时间相关的，以适应轨迹的变化。最初通过采样图像特征进行初始化，然后由神经网络进行更新。

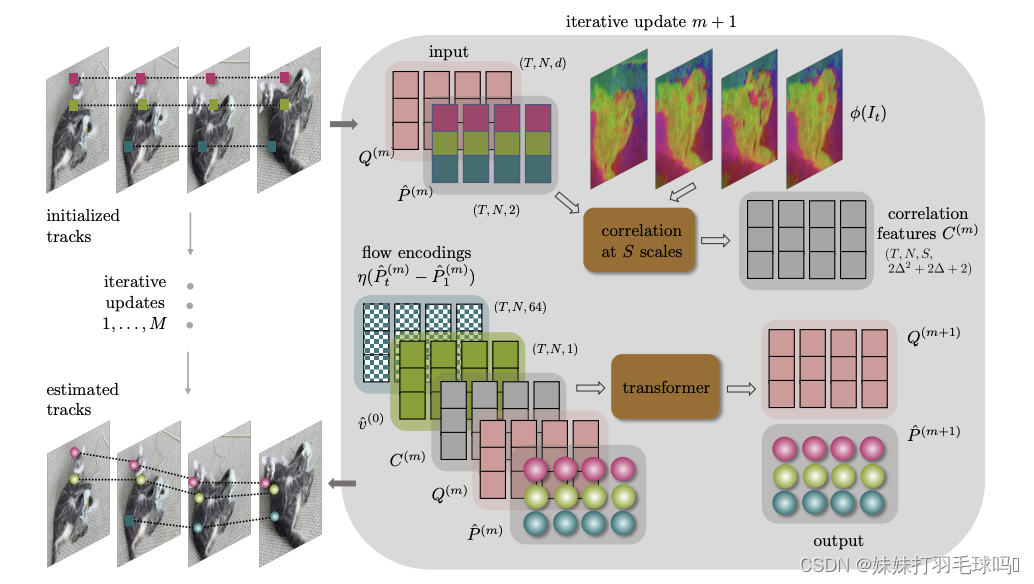
上图为CoTracker 架构。展示了一个滑动窗口和$M$次迭代更新的可视化。在一次迭代中，我们更新点轨迹$\hat{P}(m)$和轨迹特征$Q(m)$。对于所有滑动窗口，$Q(0)$初始化为$Q$，$\hat{P}(0)$初始化为未见过的帧的起始轨迹，并对上一滑动窗口中处理过的帧进行预测。可见性$\hat{v}$在最后一次更新$M$后计算。

特征$Q_t^i$的计算过程如下：

1. 初始化：首先，对于每个轨迹$i$和时间$t$，我们使用初始图像特征$\varphi (I_{t^i};s)$来初始化轨迹特征$Q_t^i$，其中$t^i$是轨迹$i$的起始时间。注意，$s$是缩放版本的索引，用于提取不同尺度的特征。
2. 神经网络更新：接下来，我们使用神经网络来更新轨迹特征$Q_t^i$。在代码中，这个神经网络是CoTracker模型中的一部分，使用Transformer网络来对轨迹特征进行迭代更新。

具体来说，轨迹特征$Q_t^i$是通过在每个时间步上应用神经网络层来更新的。这个神经网络层可能包含一些线性变换、非线性激活函数和归一化操作，具体的网络结构和参数是根据CoTracker模型的设计来确定的。

3. 相关特征

为了便于将轨迹与图像匹配，引入相关特征$C_t^i\in R^S$。这些特征通过比较轨迹特征Q和围绕当前轨迹位置${\hat{P}}_i^t$的图像特征$\varphi (I_t;s)$获得。具体地，向量 ${\hat{C}}_t^i$通过堆叠内积得到如下计算所示：

$$<Q_t^i,\varphi (I_t;s)[{\hat{P}}_t^i/ks+\delta ]>，s=1,...,S,\delta \in Z^2，||\delta |{|}_1\le \Delta ，\Delta \in N$$

其中偏移量$\delta$定义了点${\hat{P}}_i^t$ 的邻域。图像特征$\varphi (I_t;s)$是通过双线性插值和零填充在非整数位置采样得到的。${\hat{C}}_t^i$的维度为$2({\Delta }^2+\Delta )+1)S=164$，对于选择的$S$为 $S=\Delta =4$。

具体的计算过程如下：

1. 对于轨迹$i$和时间$t$，获取图像特征$\varphi (I_t;s)$，其中$s=1,...,S$是缩放版本的索引。这些缩小的特征是通过对$s\times s$邻域内的基本特征应用平均池化得到的，其中$S=4$。
2. 确定偏移量$\delta$：偏移量$\delta \in {\mathbb{Z}}^2$定义了点${\hat{P}}_i^t$的邻域。具体来说，对于每个$s$，我们在${\hat{P}}_i^t/ks$周围的邻域内选择偏移量$\delta$，并且满足$||\delta |{|}_1\le \Delta$，其中$\Delta \in \mathbb{N}$是选择的参数。
3. 通过堆叠内积计算${\hat{C}}_t^i$：对于每个$s$和$\delta$的组合，我们计算$Q_t^i$与$\varphi (I_t;s)[{\hat{P}}_i^t/ks+\delta ]$之间的内积。注意，$\varphi (I_t;s)[{\hat{P}}_i^t/ks+\delta ]$表示在图像特征$\varphi (I_t;s)$中通过双线性插值和零填充在非整数位置采样得到的值。
4. 最终的${\hat{C}}_t^i$：将所有$s$和$\delta$的组合得到的内积结果堆叠在一起，得到向量${\hat{C}}_t^i\in {\mathbb{R}}^S$。根据论文中的描述，${\hat{C}}_t^i$的维度为$2({\Delta }^2+\Delta )+1)S=164$（当$S=\Delta =4$时）。

这样，我们就得到了相关特征${\hat{C}}_t^i$，它度量了轨迹特征$Q_t^i$与图像特征$\varphi (I_t;s)$之间的相关性。这种相关性的度量对于将轨迹与图像进行匹配和跟踪是非常重要的，因为它帮助模型在视频中找到与轨迹相关的图像区域，并用于更新轨迹的估计。

代码示列：

import torch
import torch.nn.functional as Fdef compute_correlation_features(Q, image_features, grid_size, delta_range):"""Compute the correlation features for the given track features Q and image features.Args:Q (torch.Tensor): Track features tensor of shape (N, d), where N is the number of tracks and d is the feature dimension.image_features (torch.Tensor): Image features tensor of shape (S, d, H, W), where S is the number of scales, d is the feature dimension,H is the height, and W is the width.grid_size (int): Size of the grid used for correlation features calculation.delta_range (int): Maximum range of offsets (delta) used for correlation features calculation.Returns:torch.Tensor: Correlation features tensor of shape (N, S, grid_size, grid_size)."""N, d = Q.shapeS, _, H, W = image_features.shape# Reshape Q to (N, 1, 1, d) and image_features to (1, S, d, H, W) to enable element-wise multiplicationQ_reshaped = Q.view(N, 1, 1, d)image_features_reshaped = image_features.view(1, S, d, H, W)# Initialize correlation features tensorcorrelation_features = torch.zeros(N, S, grid_size, grid_size, device=Q.device)# Loop over grid positions and delta offsets to compute correlation featuresfor dy in range(-delta_range, delta_range+1):for dx in range(-delta_range, delta_range+1):delta = torch.tensor([dy, dx], dtype=torch.float32, device=Q.device)delta_scaled = delta / (grid_size * 8)  # Scale the delta to match the grid size# Compute the indices for the correlation gridgrid_y, grid_x = torch.meshgrid(torch.arange(grid_size, device=Q.device),torch.arange(grid_size, device=Q.device))grid_indices = torch.stack((grid_y, grid_x), dim=-1).view(1, 1, grid_size, grid_size, 2)grid_indices = grid_indices.repeat(N, S, 1, 1, 1).float()# Compute the image features at the grid positions using bilinear interpolationgrid_positions = (Q_reshaped + delta_scaled).view(N, 1, 1, 1, 2)  # Add delta to Q and reshape for broadcastingimage_features_grid = F.grid_sample(image_features_reshaped, grid_positions,mode='bilinear', padding_mode='zeros')# Compute the correlation features by element-wise multiplication and summingcorrelation_feature = torch.sum(Q_reshaped * image_features_grid, dim=-1)  # Element-wise multiplication and sum along the feature dimensioncorrelation_features[:, :, (grid_size-1)//2+dy, (grid_size-1)//2+dx] = correlation_feature.squeeze(-1)return correlation_features# Example usage
N = 10  # Number of tracks
d = 256  # Feature dimension
S = 4  # Number of scales
H, W = 128, 128  # Height and width of the image features
grid_size = 7  # Size of the grid for correlation features
delta_range = 4  # Maximum range of offsets (delta)# Create random track features and image features (for demonstration purposes)
Q = torch.rand(N, d)
image_features = torch.rand(S, d, H, W)# Compute correlation features
correlation_features = compute_correlation_features(Q, image_features, grid_size, delta_range)
print(correlation_features.shape)  # Output shape: (N, S, grid_size, grid_size)

补充：堆叠内积计算如下

滑动窗口推断

Transformer 设计的一个优势是它可以轻松支持滑动窗口应用，以处理非常长的视频。特别考虑一个长度为$T^{\prime }>T$的视频$V$，其长度超过了架构支持的最大窗口长度$T$。

为了在整个视频$V$中跟踪点，将视频分成 $J=\lceil 2T^{\prime }/T-1\rceil$个长度为$T$的窗口，其中窗口之间有 $T/2$ 帧的重叠。

为了处理视频，将 Transformer迭代 $MJ$次：第一个窗口的输出被用作第二个窗口的输入，依此类推。用 $(m,j)$ 上标表示迭代于第$j$个窗口的第$m$次 Transformer 更新。

因此，得到了一个 $M\times J$ 的量$({\hat{P}}^{(m,j)},{\hat{v}}^{(m,j)},Q^{(m,j)})$，横跨 Transformer 迭代和窗口。从$m=0$和 $j=1$ 开始，我们使用式 (1) 初始化这些量。然后，将 Transformer迭代M次，以获得状态 $({\hat{P}}^{(M,1)},{\hat{v}}^{(M,1)},Q^{(M,1)})$。从这个状态开始，为第二个窗口初始化$({\hat{P}}^{(0,2)},{\hat{v}}^{(0,2)},Q^{(0,2)})$，方式类似于式 (1)。具体来说，${\hat{P}}^{(0,2)}$ 的前$T/2$ 个分量是 ${\hat{P}}^{(M,1)}$ 的后 $T/2$ 个分量的副本；${\hat{P}}^{(0,2)}$的后 $T/2$个分量是 ${\hat{P}}^{(M,1)}$ 中 $t=T/2-1$ 时刻的副本。${\hat{v}}^{(0,2)}$ 的更新规则与此类似，而 $Q^{(0,j)}$总是使用初始轨迹特征 Q 进行初始化。在初始化 $({\hat{P}}^{(0,2)},{\hat{v}}^{(0,2)},Q^{(0,2)})$ 后，将 Transformer 再次迭代M次于第二个窗口，然后继续为下一个窗口重复该过程。最后，通过使用初始化 (1) 来扩展令牌格，添加任何新的轨迹。

展开学习

论文发现以展开的方式学习窗口式 Transformer 对于适当处理部分重叠的窗口很重要。主要的损失是轨迹回归损失，通过迭代 Transformer 应用和窗口进行求和：

$$L_1(\hat{P},P)=\sum _{j=1}^J\sum _{m=1}^M{\gamma }^{M-m}||{\hat{P}}^{m,j}-P^{(j)}||，(2)$$

其中$\gamma =0.8$是用于衰减早期 Transformer 更新的因子。这里，$P^{(j)}$包含了限制在窗口$j$中的真实轨迹（从窗口中间开始的轨迹向后填充）。第二个损失是可见性标志的交叉熵损失：$L_2(\hat{v},v)={\sum }_{j=1}^{J}CE({\hat{v}}^{(M,j)},v^{(j)})$。

在训练过程中，由于计算成本的原因，损失只对少量的窗口进行求和。但在测试时，可以任意展开窗口式 Transformer迭代，从而原则上处理任何视频长度。

展开推断允许跟踪后出现的点，只在点首次出现的滑动窗口开始跟踪点。同时，确保这样的点在训练数据中存在，通过在序列的中间帧中采样可见的点。

Transformer

Transformer 由交错的时间注意力块和组注意力块组成，两者都应用到输入和输出上的两个线性层。通过在时间和点轨迹之间分解注意力，使得模型的计算变得可行：复杂性从 $O(N^2{T}^2)$ 减少到 $O(N^2+T^2)$。除了输入估计轨迹的位置编码$\eta$外，此外还添加了标准的正弦位置编码：时间维度为 1 维，空间维度为 2 维。