💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码及数据

---

💥1 概述

基于水循环算法（Water Cycle Algorithm，WCA）优化的核极限学习机（KELM）回归预测是一种将WCA和KELM相结合的方法，用于提高回归预测的性能和准确度。

WCA是一种模拟水循环过程的优化算法，通过模拟水的蒸发、降水和径流等过程来搜索最优解。它具有全局搜索和自适应调整参数的能力，能够有效地优化复杂的非线性问题。

在WCA-KELM方法中，首先使用WCA来搜索最优的核函数参数和KELM的超参数。WCA通过不断迭代的过程，根据每个个体的适应度值来更新个体的位置和速度，以寻找最优解。在每次迭代中，根据适应度值的大小，更新个体的位置和速度，直到达到停止条件。

在优化过程中，WCA-KELM通过搜索最优的核函数参数和KELM的超参数，进一步提高了KELM的回归预测性能。通过优化核函数参数，可以更好地捕捉输入数据的非线性特征；通过优化KELM的超参数，可以调整模型的复杂度和泛化能力。

基于水循环算法优化的核极限学习机回归预测是一种将WCA和KELM相结合的方法，用于提高回归预测的性能和准确度。通过WCA的全局搜索和自适应调整参数的能力，可以优化核函数参数和KELM的超参数，进一步提高KELM的回归预测性能。在实际应用中，WCA-KELM可以应用于各种回归预测任务，并具有较好的性能表现。

📚2 运行结果

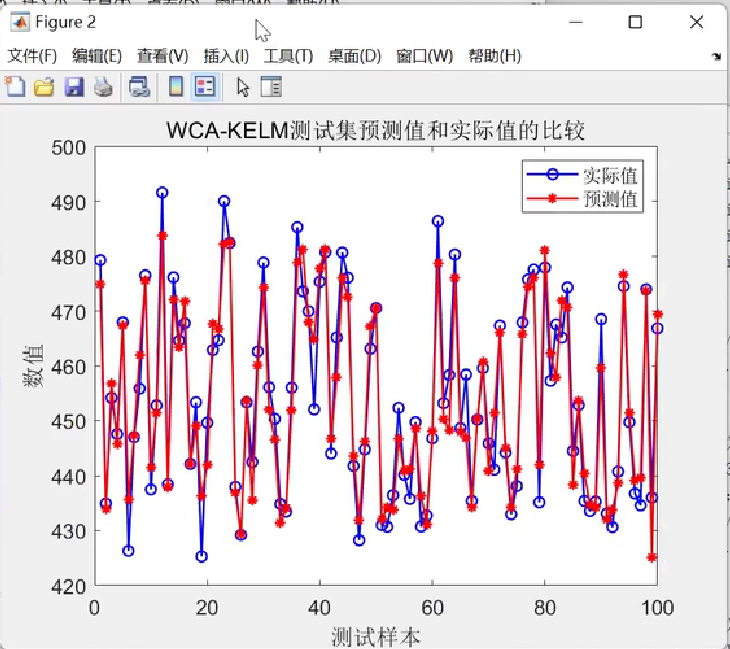
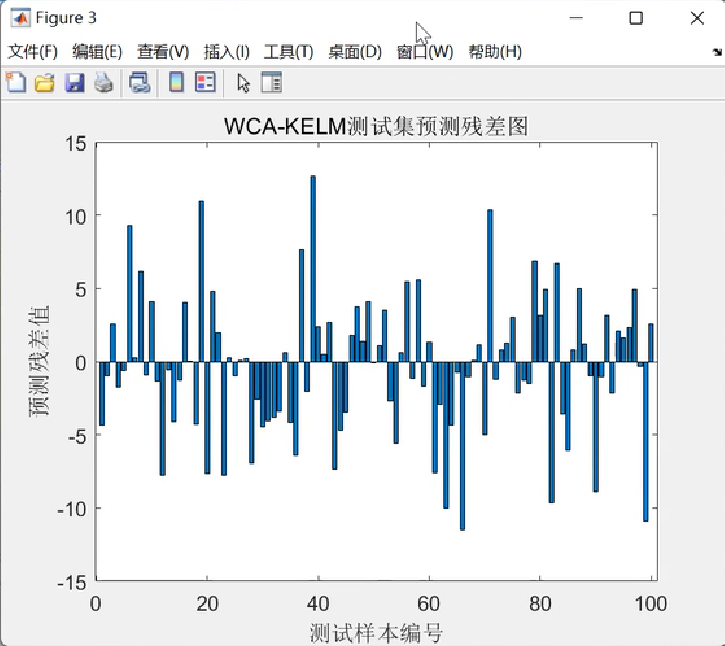
🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]周志琴.基于优化的核极限学习机在负荷预测中的研究[D].广东工业大学,2017.DOI:10.7666/d.D01243248.

[2]任瑞琪,李军.基于优化核极限学习机的中期电力负荷预测[J].测控技术, 2018, 37(06):20-24.DOI:10.19708/j.ckjs.2018.06.003.

[3]马飞燕,李向新.基于改进麻雀搜索算法-核极限学习机耦合算法的滑坡位移预测模型[J].科学技术与工程, 2022(005):022.

🌈4 Matlab代码及数据