模式识别——贝叶斯决策理论BDR
- 须知
- 基本原则
- 0-1损失下的BDR
- MAP(极大后验)
- log trick
须知
所有内容在分类问题下讨论。
基本原则
定义
- X X X为观测
- Y Y Y为状态
- g ( x ) g(x) g(x)用 x x x对 y y y进行预测
- 预测损失为 L [ g ( x ) , i ] L[g(x),i] L[g(x),i]
风险 R i s k Risk Risk为损失的期望,即对所有观测造成的损失的平均,即对大量观测判别的损失最低:
R i s k = E X , Y [ L ( X , Y ) ] = ∫ ∑ i = 1 M P Y , X ( i , x ) L [ g ( x ) , i ] d x R i s k=E_{X,Y}[L(X,Y)]=\\ \int\sum_{i=1}^{M}P_{Y,X}(i,x)L[g(x),i]d x Risk=EX,Y[L(X,Y)]=∫i=1∑MPY,X(i,x)L[g(x),i]dx
通过条件概率展开成如下形式:
R i s k = E X [ R ( x ) ] = ∫ P X ( x ) R ( x ) d x Risk=E_X[R(x)]\\ =\textstyle\int P_{X}(x)R(x)d x Risk=EX[R(x)]=∫PX(x)R(x)dx
其中 R ( x ) R(x) R(x)为条件风险,即给定观测下的风险:
R ( x ) = ∑ i = 1 M P Y ∣ X ( i ∣ x ) L [ g ( x ) , i ] R(x)=\sum_{i=1}^{M}P_{Y|X}(i\mid x)L[g(x),i] R(x)=i=1∑MPY∣X(i∣x)L[g(x),i]
我们的目标就是找一个最优的判别函数,在观测 x x x给定的情况,使得对状态的预测损失最小。
g ∗ ( x ) = arg min g ( x ) R ( x ) g^{*}(x)=\arg\operatorname*{min}_{g(x)}R(x) g∗(x)=argg(x)minR(x)
gpt给出的使用条件风险代替全局风险的原因,可以参考:

0-1损失下的BDR
通过推导可以得出结论,0-1损失下的BDR就是MAP(极大后验准则),这是非常符合认知的:
g ∗ ( x ) = a r g m a x i P Y ∣ X ( i ∣ x ) {\mathcal{g}}^{*}(x)=argmax_{i}P_{Y|X}(i\mid x) g∗(x)=argmaxiPY∣X(i∣x)
对应的损失为:
R ∗ = ∫ P Y , X ( y ≠ g ∗ ( x ) , x ) d x R^{*}=\int P_{Y,X}(y\neq g^{*}(x),x)d x R∗=∫PY,X(y=g∗(x),x)dx
MAP(极大后验)
考虑二分类问题,使用极大后验可以表示为:

使用贝叶斯公式对极大后验展开,由于展开后的分母相同可以约掉(观测x已知),可以得到:
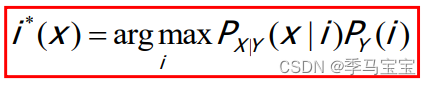
log trick
两边取对数等价,可以将决策函数化为以下形式,以简化计算: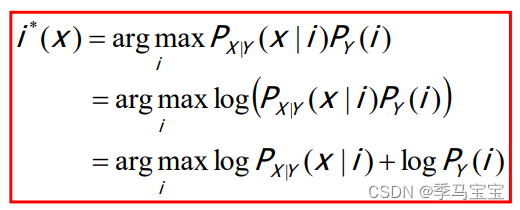
总而言之:
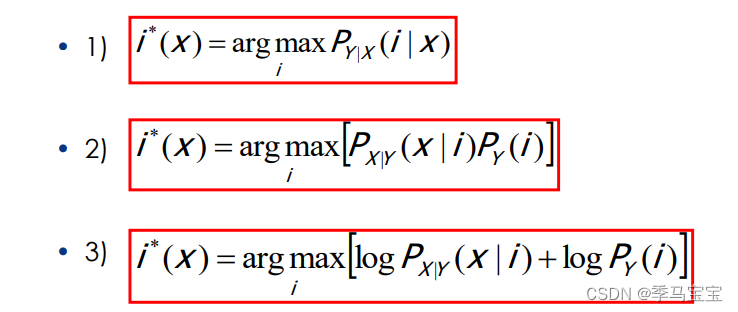








)




 等级考试试卷(一级))





)