@[TOC]([swift刷题模板] 树状数组(BIT/FenwickTree) )
一、 算法&数据结构
1. 描述
- [python刷题模板] 树状数组
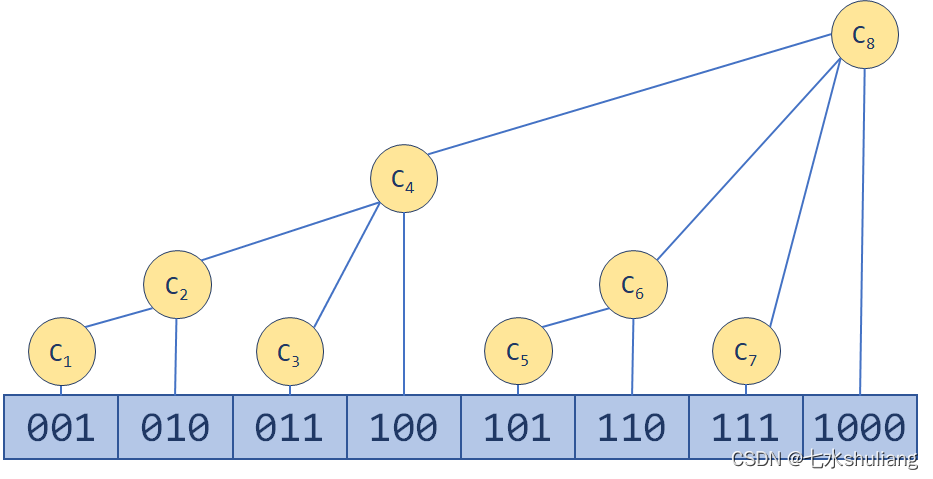
二、 模板代码
1. 单点赋值(增加),区间求和(PURQ)
例题: 307. 区域和检索 - 数组可修改
class BIT {var c: [Int]var n: Int init(_ n: Int){c = Array(repeating:0, count: n + 1)self.n = n }func add(_ i: Int, _ v: Int){var i = i while i <= n {c[i] += v i += i & -i }}func sum(_ i: Int) -> Int {var i = i var s = 0 while i > 0 {s += c[i] i &= i - 1}return s}
}class NumArray {let tree: BIT var nums: [Int]init(_ nums: [Int]) { tree = BIT(nums.count + 1)self.nums = nums for (i, v) in nums.enumerated() {tree.add(i + 1, v)}} func update(_ index: Int, _ val: Int) {tree.add(index+1, val - nums[index])nums[index] = val}func sumRange(_ left: Int, _ right: Int) -> Int {return tree.sum(right + 1) - tree.sum(left) }
}
- 以下待施工
2. 区间更新,单点询值(RUPQ)
例题: 1589. 所有排列中的最大和
这题其实应该用差分数组,可以省一层log。思想就是树状数组的IUPQ模型。
树状数组经典案例,要用差分数组理解:
这个实际上是用树状数组维护原数组的差分数组c[i]=a[i]-a[i-1]
求原数组的值a[i]实际上是差分数组的前缀sum(c[0]…c[i]),所以get a[i]可以用sum c[i]表示,
而原数组a区间[x,y]更新+v,产生的效果是:x位置比x-1位置大了v,y+1位置比y小了v;
对差分数组c来说,产生变化的就是c[x]增加了v,c[y+1]减小了v,因为c数组代表的是a中每个数比前一个数的差。
- sum[i]代替get[i],单点求值
- 两步add(l,v)和add(r+1,-v),区间更新
3.区间更新,区间求和(RURQ)
题目: P3372 【模板】线段树 1
- 记sigma(r,i)表示r数组的前i项和。
- 我们知道,在区间求和的BIT中,实际维护了原数组a的差分数组d。
- 于是有a[n] = d[1]+d[2]+…+d[n]
- 观察式子:
a[1]+a[2]+…+a[n]
= (d[1]) + (d[1]+d[2]) + … + (d[1]+d[2]+…+d[n])
= n * d[1] + (n-1) * d[2] +… +d[n]
= n * (d[1]+d[2]+…+d[n]) - (0 * d[1]+1 * d[2]+…+(n-1) * d[n])(式子①)
维护一个数组d2[n],其中d2[i] = (i-1)*d[i]
每当修改c的时候,就同步修改一下d2,这样复杂度就不会改变
那么 sigma(a,n) = 式子①=n*sigma(d,n) - sigma(d2,n)
5. 单点更新区间求极值
例题: CF522 D. Closest Equals
这是20220923的茶。
- 相同元素组成可以看成线段,问题转化为求区间内最短线段。
- 询问离线,按r排序,计算每个线段长度,记在左端点上。
- 查询区间最小值即可。
- 正常用线段树,但是py线段树过不了,于是上网查了个树状数组的模板
6. 单点赋值,区间询问最大(LIS II)
例题: 2407. 最长递增子序列 II
周赛T4,当时用线段树做的;实际测试线段树的表现甚至优于树状数组,奇怪极了。
7. 二维树状数组(IUPQ)
例题: 6292. 子矩阵元素加 1
- 周赛T2,这题卡一维树状数组;但是可以差分过;可以二维树状数或二维差分过。

.css()方法设置元素css样式问题随记)


第六周实验:全加器)
![[转]x86_64的基本架构](http://pic.xiahunao.cn/[转]x86_64的基本架构)








)




