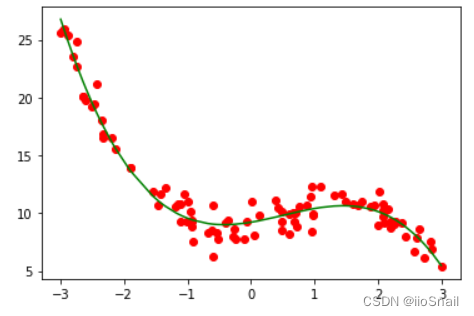
昨天一个客户要在RK3399 Linux开发板上面使用身份证读卡器,由于没有客户的开发板,故只能用本机ubuntu虚拟机来交叉编译,用客户发过来的交叉编译工具,已经编译好libusb然后编译libdonsee.so的时候提示找不到libusb,报错如下图。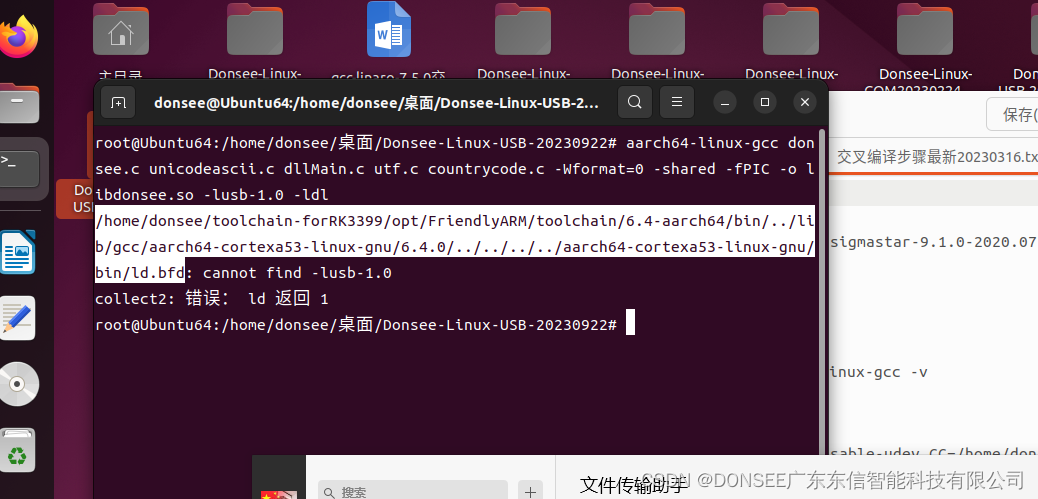
解决办法:
1.把编译好的libusb-1.0(含里面的libusb.h)文件夹拷贝到交叉编译器include文件夹里面
2.把编译好的libusb-1.0.a 到编译器的lib文件夹里面。cp /home/eastcoms/libusb/lib/libusb-1.0.*
我是所有libusb-1.0开头的所有文件都复制过去。
操作了上面两步即可完成编译读卡库libdonsee.so