文章目录
- 写在前面
写在前面
本文是论文A Survey on Over-the-Air Computation的阅读笔记:


通信和计算通常被视为独立的任务。 从工程的角度来看,这种方法是非常有效的,因为可以执行孤立的优化。
然而,对于许多面向计算的应用程序,主要关注的是设备上的本地信息的函数,而不是本地信息本身。
在这种情况下,信息论的结果表明,利用多址信道中的干扰进行计算,即空中计算(OAC)可以提供比分离通信和计算任务更高的计算速率。
而且,随着参与节点的增加,OAC和Department方案在计算速率方面的差距也越来越大。 基于这一动机,在本研究中,我们对实际的OAC方法进行了全面的综述。 在概述了与OAC相关的基本原理之后,我们讨论了可用的OAC方案及其优缺点。 我们概述了在无线信道中实现可靠计算的使能机制。 最后,我们总结了OAC的潜在应用,并指出了未来的发展方向。
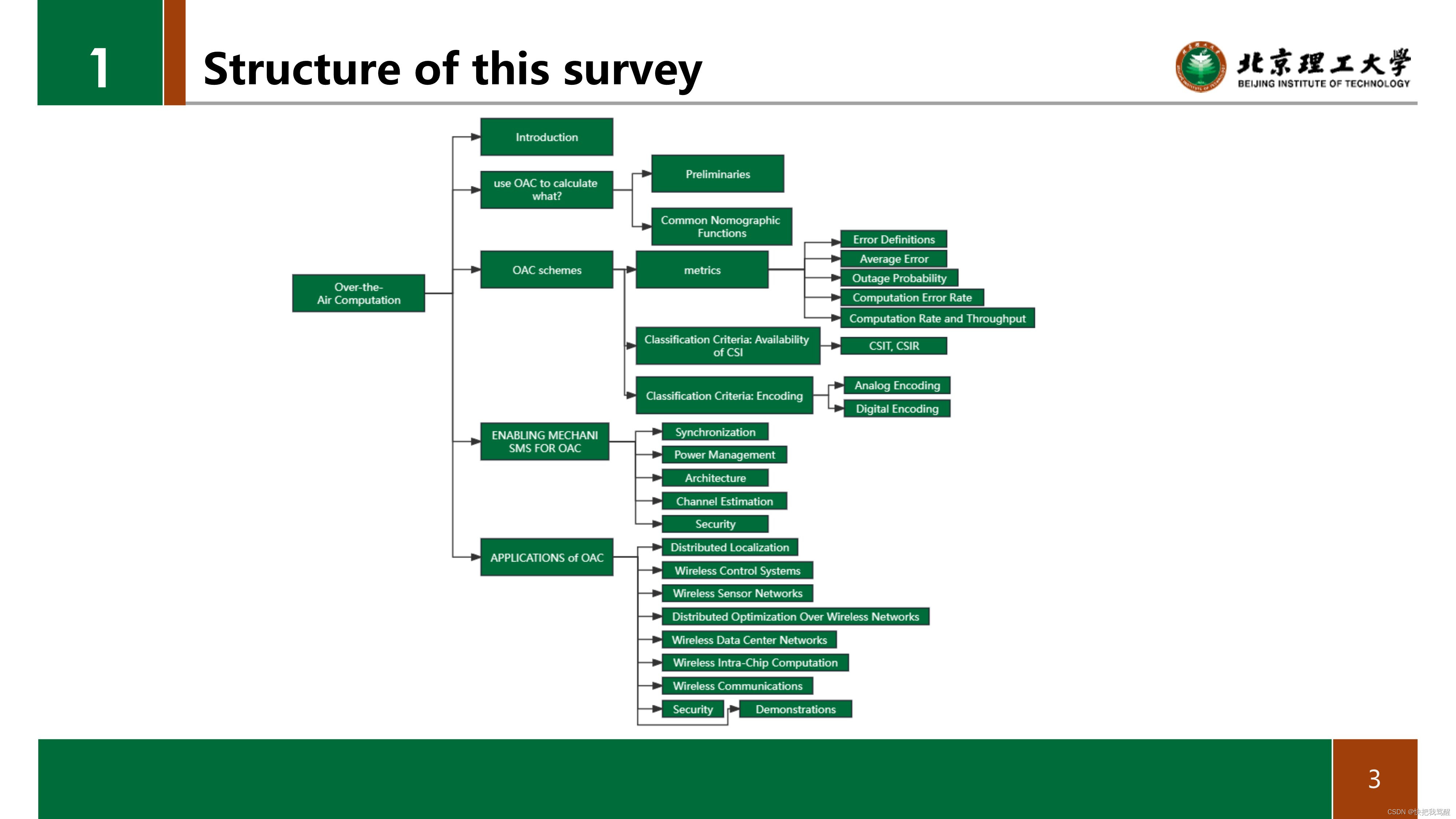
文章的结构


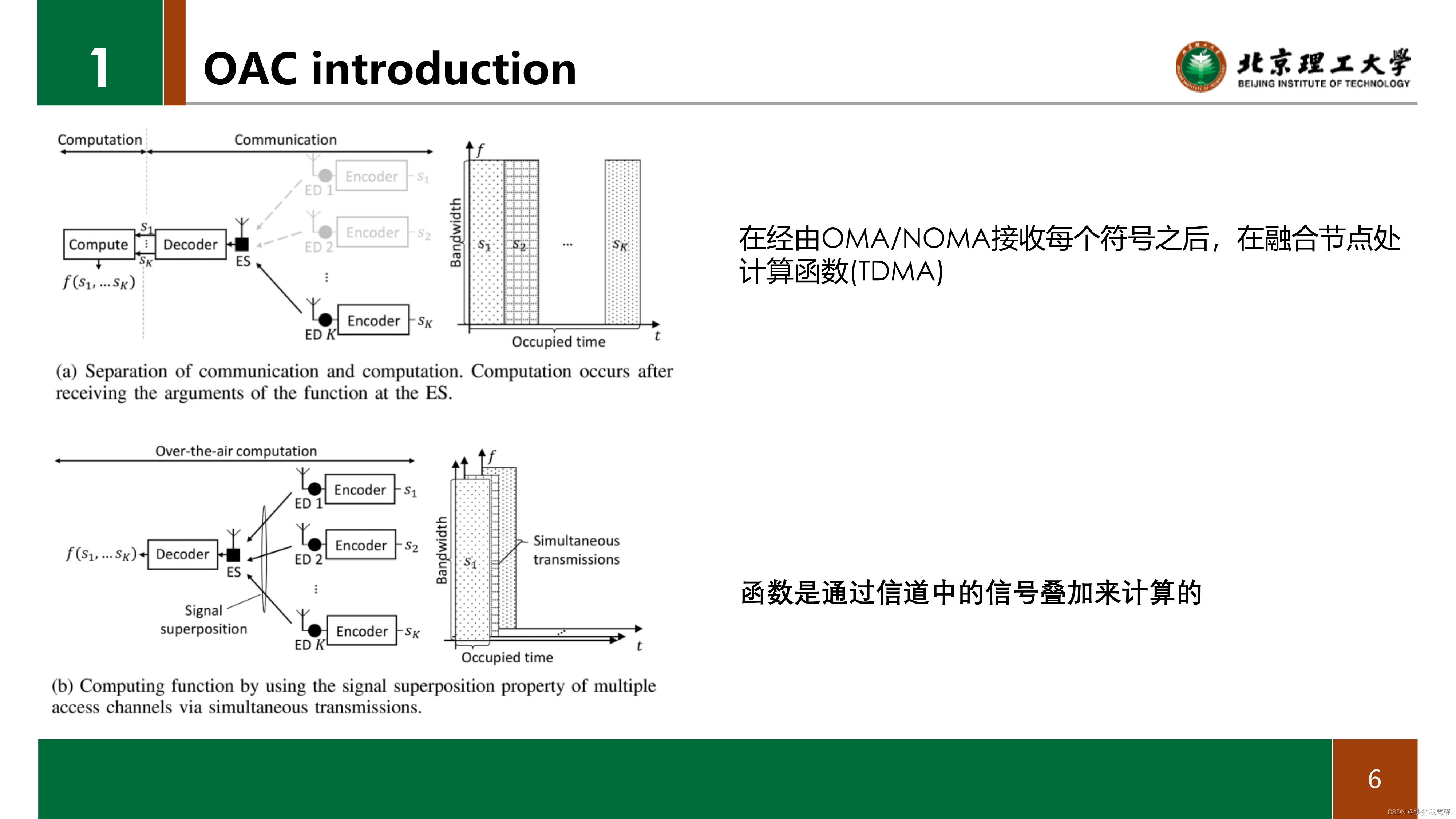
空中计算(OAC)是利用无线多址信道的信号叠加特性进行数学函数的计算。 OAC的显著特征是不通过正交信道获取边缘设备(如智能手机、膝上型计算机、平板电脑、车辆或传感器)处的本地数据以在融合节点(如基站或接入点处的边缘服务器)处执行计算任务。 相反,是通过同时传输并利用干扰来处理计算。 例如,假设目标是在ES(Edge Server)处求出函数F(S1,…,SK),其中SK是第K个ED(Edge Divice)处的符号。
从右面往左面看:
在通信和计算任务分离的情况下,在经由正交或非正交资源(即,正交多址(OMA)和非正交多址(NOMA))接收每个符号之后,在融合节点处计算函数,如图中的时域多址(TDMA)所示 1(a).
另一方面,在OAC中,函数是通过信道中的信号叠加来计算的,如图所示 1(b). 在这个例子中,关键的观察是,如果ES对本地信息不感兴趣,而只对它们的一个函数感兴趣,那么OAC为减少资源使用铺平了道路,否则资源使用会随着EDS的数量而增加。 因此,它对独立处理计算和通信任务的传统方式是一个根本性的、颠覆性的概念。





OAC的目标是通过依赖其表示来计算多元函数,该表示能够在结构上与多访问通道自然执行的底层操作相匹配。
在无线通信中,多接入信道具有可加性,即信号叠加特性。
有了这个属性,OAC问题可以归结为目标函数的一种表示方式,该表示方式是一个特殊的函数,称为nomographic函数,或多个无线资源上的nomographic函数集。
这些函数被称为列线图,因为它们与通过某些图(即模拟计算)解某些方程的列线图是内联的。
诺莫图的一个著名例子是史密斯图,它有助于解决与传输线有关的问题。虽然列线图允许快速和准确的计算,但由于数字计算机的有效性,列线图的使用案例在历史上减少了。
然而,关于nomography的基本理论是复杂的,可以说与神经网络有关,并为解决数字计算受延迟、功耗和有限的通信带宽影响的场景铺平了道路。在这一节中,我们讨论了关于列线图函数的初步研究,以揭示用OAC可以计算出什么。

定义1: (nomographic函数) 假设S^K, K>2, 是一个紧的度量空间。存在前处理函数和后处理函数,f可以表示为
方程(1)可以解释为理想上行链路(UL)信道中函数f的估计((i.e., no noise, no multi-path channel distortion)
SK和φ(内)K是第k个数据传递节点的符号和预处理函数(内函数),
来自K个节点的信号之和对应于信道中自然发生的叠加,
φ(外)后处理函数(外函数)· 是融合中心的后处理功能
值得注意的是,定义1中提到的紧性是一个重要的假设。 例如,连续函数F(S1,S2,…,SK)在紧空间SK上的值域是紧的。 因为函数是有界的,所以可以保证极限的存在,或者保证上界和下界被函数所占据。
从OAC的角度来看,紧凑性是由于实际的限制而继承的。 例如,传感器的测量空间通常是紧凑的,因为传感器可以在有限的封闭区间内量化值,
诺图函数的空间,带有连续的前,后处理函数的约束的表示诺图函数的空间,连续函数的空间;可以被表示为:EK,N(Ek) N0(Ek) C0(Ek)

Theorem1 每个函数f∈C0(EK)都可以用实的、单调递增的预处理函数表示,也可以用不连续的后处理函数表示。
Theorem2 每一个函数f∈F(ek)都是列示的nomographic(即n(ek)=F(ek))(任意的一个诺莫函数的函数都可以表示成带有连续前置处理函数约束的诺莫函数的形式)
Definition 2 如果预处理函数是固定的,预处理函数是通用的,他们可以用来计算F(EK)中的每个函数。 通用性是OAC的一个理想属性,因为如果目标函数随时间变化,预处理函数不需要重新设计(即减少通信开销)。这个特性在[2],[34]中被用于多集群计算,如第四节-c中所讨论的。它还提到,通用性提供了对网络拓扑变化(通过删除和连接设备)的鲁棒性,因为传输节点不需要调整其预处理功能。
Theorem 3 N0(EK)在C0(EK)中无处致密

Theorem 4 每一个函数f∈C0(EK)都可以表示为N0(EK)中至多2k+1个诺图函数的叠加,即,(f(。)=。。。。。)
其中,后处理函数ϕ依赖于f,而前处理函数ψk独立于f。
在几何上,上述公式中的2k+1内和保证了s1,…∈EK和(ϕ1(k=1 ψk (sK)),…ϕ2K+1(k=1 ψk (sk))∈R2K+1连续双射对应的存在性。因此,内和描述了一个连续将EK嵌入到R(2K+1)中的同胚函数。在[46]中,Sternfeld增强了定理4的表述,证明了上述公式(2)中的2K +1个 nomographic函数不能被简化来表示每个f∈C0(EK)。因此,从OAC的角度来看,定理4意味着至少需要分配2K +1个无线资源,其中每个资源都专用于N0(EK)中的一个nomographic函数,以计算C0(EK)中的每个函数。
在数学中,定理4,也被称为Kolmogorov叠加或Kolmogorov- arnold表示定理,因为它解决了[47]中希尔伯特的第十三问题的一个更受约束的(即函数f需要是连续的),但一个更一般的形式(即,只有一个变量函数的叠加)。还有其他变体的Kolmogorov的叠加和建设性证明,展示了如何获得预处理和后处理函数。要全面地讨论这些变体和结构,我们请读者参考[48,Ch。2]。OAC文献[2]中提到的一个变体如下。

Theorem 5对于每一个函数f∈C0(EK),在N0(EK)中存在2k+1个诺模函数,使得 f( … ) = …映射成
立,当预处理函数φ是定义良好的、连续的、单调的且与f无关时,系数αk、任意k、β是适当的非负实常数。
文[2]在定理5的基础上所做的主要观察是:对于2k+1资源的连续的列线函数,计算C0(EK)中的每一个函数,预处理函数可以设计为普适的。 注意,(3)中的叠加涉及2k+1个后处理函数和一个单一的前处理函数。 在文献中,通过引入对(3)中后处理函数的变元的转移,证明了叠加也可以用[48,th.1]和[50,th.2.14]中讨论的单个前处理函数和单个后处理函数来表示。 另外,Kolmogorov的叠加可以解释为一种特殊的前馈神经网络,并有助于预测神经网络的复杂性(参见[51]、[52]、[53]中的讨论)。
在某些情况下,可能希望不消耗2k+1无线资源来计算具有2k+1连续列线函数的特定连续函数。 在这种情况下,可以遵循两个不同的方向之一:操纵目标函数的定义域或构造逼近目标函数的列线函数。 在第一种方法中,部分区域被裁剪,这样就可以用连续的前处理和后处理函数计算出列线函数。 例如,如果对于α∈(0,1)选择S为[α,1],则几何平均值可以用S上的φ_k(x)=ln(x),k,和φ(x)=e^(x/k)的一个诺图函数来计算。在第二种方法中,诺图逼近可以定义如下[2]:

Definition 3 线图逼近 设 \epsilon > 0 为任意常数。 关于精度的可逼近的线图函数空间定义为 f(…) = … ,如果f∈N0(EK),我们写 。。。。
例如,在定义3下,EK上的几何平均值是N0(EK)中的一个函数,因为当P0()>0时,它可以近似为φk(x)=ln(x+1/P0())和参数=ex/k。 然而,由于可以用不同的方法来定义逼近线图函数的空间,逼近线图函数的完全刻画仍然是一个需要更多研究的领域。 例如,在[54,eq.(5)]中,近似的列图函数是以随机的方式定义的。 关于近似列线图的进一步理论研究,读者还可参考[54],[55],[56],[57]。

Definition 4 对称函数 设σ:SK→SK表示置换。 函数F:SK→R,它对其自变量的排列是不变的,即:
对称函数空间的一个显著特征是,只有数据本身是重要的,而不是它的原点。 从应用的角度来看,许多函数,如均值、最大值、最小值、中值和多数票(MV)都属于这类函数,这些函数要么具有精确的或近似的线图函数。 第二个重要特征是通过类型函数,即频率直方图[9]、[10]、[58]、[59]可以计算出该空间中的函数。 类型函数可以定义为指示函数的多重加权算术和,即基于某一集合计算设备的数量,在[9]、[10]中也研究了基于类型的多址接入(TBMA)。

在表I中,我们列出了文献中讨论过的几个精确和近似的线图函数。 算术平均、加权求和和Majority Vote在分布式学习应用中得到了广泛的应用,而在物理层网络编码中经常出现模2求和。 在[60]中,乘积操作用于密钥生成。 在WSN中使用最大值、最小值和计数函数(例如,如果温度上升,则生成警报)或计算直方图(例如,用TBMA[9]、[10]]计算测量统计量)。 几何平均、p-范数和多项式函数经常被提到,以提供可以在无线网络上计算的线图函数示例。 特别地,P范数用于计算平均池或最大池在空中在[61]。
一个有趣的方向是对给定的连续函数用连续单调的后处理函数和连续的前处理函数来计算近似的列线函数。 在[56]中,通过使用维数函数分解的组合得到了一个近似。 在这种方法中,目标函数被一个双射函数扭曲,这样得到的函数可以用一阶方差分析(ANOVA)分解很好地逼近。 为了计算斜函数,使用了Bernstein多项式。 值得注意的是,利用Bernstein多项式可以构造性地证明Weierstrass逼近定理,即每个连续函数
都可以用一个足够阶的多项式在任意有限区间上以任意精度逼近。
另一个有趣的方向是通过将目标函数表示为一个优化问题的解,并通过迭代求解该问题,这些迭代可以用一些初等列线函数表示。 例如,如第IV-E1节所讨论的,几何中值可以通过使用[62]中的Weiszfeld算法通过空中迭代计算。在[63]、[64]和[65]中,通过使用参数的二进制表示,提出了通过通信轮计算几个非线性函数,例如最大值或最小值。 例如,为了计算参数的最大值,在第一轮中,ES向EDS查询参数二进制表示的最高有效位位置中的位1。 如果对查询有任何响应,ES检测参数的最大值的最高有效位为1; 否则为0。 在第二轮中,如果检测到最高有效位为1,则ES向EDS查询最高有效位和第二有效位中的位1。 否则,ES查询第二有效位位置中位为1的所有EDS。 从对第二查询的响应中,ES确定第二有效位。 该过程继续进行,直到检测到最低有效位为止。 用参数的倒数计算最小函数也可以用同样的方法。 对于计算函数的连续分区,阅读器也参考[59]。


一种OAC方案旨在在具有保真度标准的无线多址信道(MAC)上实现(1)(OAC定义)(或(2)(科尔戈莫洛夫)。 为了对现有的OAC格式进行严格的分类和推广,考虑一个OAC格式,它的目标是计算符号向量S[n]=[S1[n],…,SK[n]]t的诺模函数Z[n]=F(S[n])_f(S1[n])_f(S1[n])_f(S1[n])_f(s1[n])_f(s1[n])_sk[n])_n,n∈{1,…,nf},nf≥1。 设sk=[sk[1],…,sk[nf]]t和pk=[pk[1],…,pk[nf]]t表示第k个Ed处的符号向量和预处理的符号向量,对于pk[n]=ík(sk[n])∈R,±n,第k个Ed计算编码向量ck∈Cb为
𝐵 是复值码字中调制符号的数目。
M是将B个调制符号映射到B个可用资源的资源映射器。
现在,考虑B个符号中的L个调制符号,由mk=[mk,1,…,mk,l]t表示,它们用线性预编码器𝑩_𝑘∈𝐶^(𝑁_𝑡×𝐿)处理为

NR是ES上的可用维数,pk∈R表示第kED的接收信号功率,它是大规模信道模型、功率控制、波形、功率放大器(PA)非线性和邻接信道泄漏比(ACLR)要求的函数(进一步讨论请参见第IV-B节)。
在ES处的接收机用线性解码器 A H ∈ C L × N r A^H∈C^L×N_r AH∈CL×Nr处理叠加向量y(例如,克服信道对叠加的影响以及bk,k)
通过使用线性解码器的𝑁_𝑎𝑐𝑐𝑒𝑠𝑠输出,资源解映射器𝑀^(−1)首先构造叠加码字 C = [ C 1 , . . . , C B ] t ∈ C B C=[C1,...,CB]t∈CB C=[C1,...,CB]t∈CB。 之后,接收机计算叠加的预处理符号的估计,作为
后处理函数对目标函数进行评估
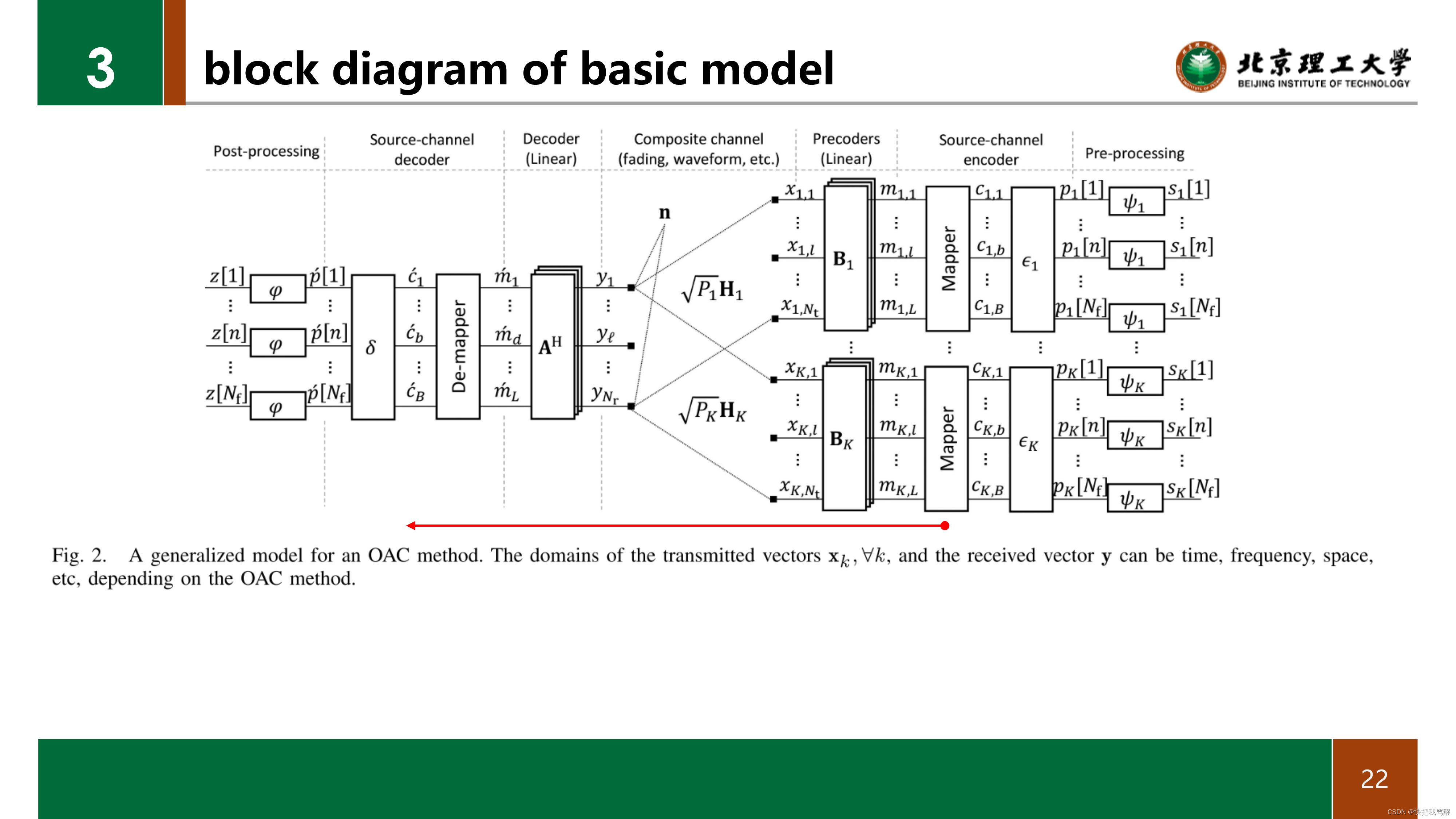
在图 2、给出了基于上述OAC发射机和接收机操作的框图。
值得注意的是,我们没有指定发送向量 x k , ∀ k x_k,\forall k xk,∀k和接收向量y的域。 在不丧失一般性的情况下,域可以是时间、频率或空间,这取决于方案。
另外,如果目标函数是基于Kolmogorov叠加的,则(2)中的2k+1个诺图函数可以用一般的OAC方案在正交资源上计算(见[36]例)。

给出定义如下
Average Error : 计算用的经典均方误差(MSE)[67],[68],归一化MSE
Outage Probability:与MSE相比,中断概率提供了计算误差的统计视图。 通过使用(12),可以将其定义为归一化费用大于或等于 epsilon[39]、[66]的概率,即。阻塞中断概率。
Computation Error Rate: 计算错误率(CER)类似于通信系统中的误码率。 当函数的自变量为离散值时,它可以用来评估计算量。 设𝑠_𝑘[n]为离散随机变量,forall k,n。 CER可以定义为 。块中断概率BCER

计算速率R和计算吞吐量R可以分别定义为每信道使用[3]、[4]、[69]计算的函数数和每秒计算的函数数。 它们可以分别表示为(如)
其中D=2NaccessNr和T是实维数和用于计算Nf个函数的间隔。值得注意的是,对于给定的带宽W和时间间隔T,单输入单输出场景的实维数大约等于2WT[70,sec.4.6]。 因此,对于S个空间流,计算吞吐量可以近似地计算为R≈2WS×R
可实现计算速率(Achievable Computation Rate 定义:设𝒔_𝒌[n]为离散随机变量 任意k,n。如果存在一个长度为B的分组码序列,使得Limb→∞PBCER=0,则称速率R是可达到的。(分组码长度无穷时,块计算错误率为0,速率可以达到)
文[7]研究了高斯信道上的模p和函数,即f(S[n])=kk=1qksk[n],对于sk[n],qk∈FP,即cb=kk=1hkck,b+nb(见图2)。 在[7,TH.2]中,对于𝑛_𝑏在实数域,Nazer和Gastpar证明了Nb∈R的可达计算速度为
(左下式)
定义6(可实现的计算速率[4]):如果存在一个方案,对于每个速率r<rcomp(f,),且每个δ>0,满足Pbout()<δ,则参数rcomp(f,)被称为fand的可实现的计算速率。
基于定义6和[1]和[7]中嵌套格码的性质,对于实值加性高斯白噪声(AWGN)信道和算术和,Goldenbaum在[4,TH.5和EQ.(54)]中证明了
其中b0(f,)是在第III-C2A节中为给定函数f定义的位数和最大失真量。
The achievable computation rate with the separation of communication and computation can be dramatically lower than the ones with OAC.

在图 3.基于文[3]中给出的算术和的例子,我们证明了在给定数目的EDs下可实现的计算速度。 假设符号s_k[n],k,n是概率为1/2的独立同分布(IID)伯努利随机变量,信噪比为15 dB。 从[71]可以计算出H(f(s[n]))=K-2-kk=1kklog2kk≤12log2(πek/2),且b0(f,)=1足以表示符号。 通信与计算分离的可达到的计算速率可计算为1 2k log2(1+kp/σ2n)[3],[72,等式(6.13)] 3、
通信与计算分离的计算速度明显低于通信与计算联合的计算速度。
ED数 K = 100, OAC承诺比分离的可靠计算快大约10倍。
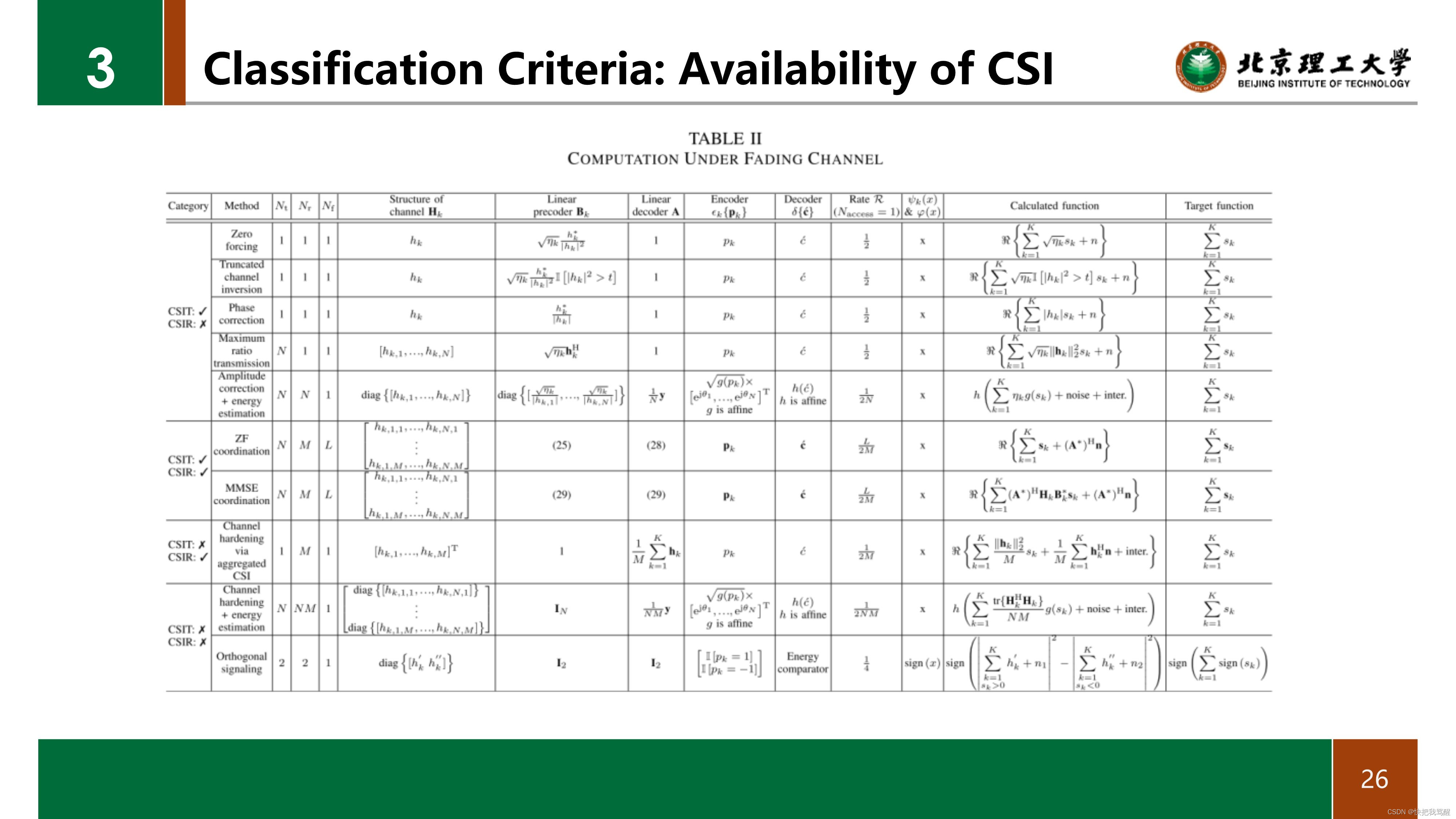
使用OAC方法计算的一个挑战是由于在叠加之前发生多径失真对来自EDS(即,H_k X_k)的发送符号的影响,如(8)所表示的。因此,估计在ES处的函数输出的估计器可能无法实现,即,它可能不只是作为接收符号的函数而被写入。 例如,考虑一个场景,其中H是IID,并且遵循瑞利衰落,并且功率控制确保平均接收信号功率完全对齐,例如,pk=1,±k。 因为在这种情况下ES处的叠加符号不能表示为
Balabala
其中H∈CNR×NT是一个独立于向量xk,±k的矩阵(即不存在一致衰落矩阵H[67]),不能实现依赖于h的可用性来获得k k=1xk的均衡器。 鉴于这一观察,在本小节中,我们根据如何通过预编码器BK、K和解码器A处理由无线信道引起的衰落对现有的方法进行分类。我们根据发射机(CSIT)和接收机(CSIR)的CSI可用性对它们进行分组。 为了简化分类,我们假定pk=1,k。 对于采用叠加符号的实部进行计算时的不同策略,我们也给出了表II中相应的方程式。

A channel reverse 为了扭转无线信道对所发送符号的影响,如果相应信道系数的绝对平方大于预先设置的阈值T,则符号与信道系数的逆相乘。
B phase correction基于信道起的相位失真量旋转所发送符号的相位来实现相干叠加的预均衡
C


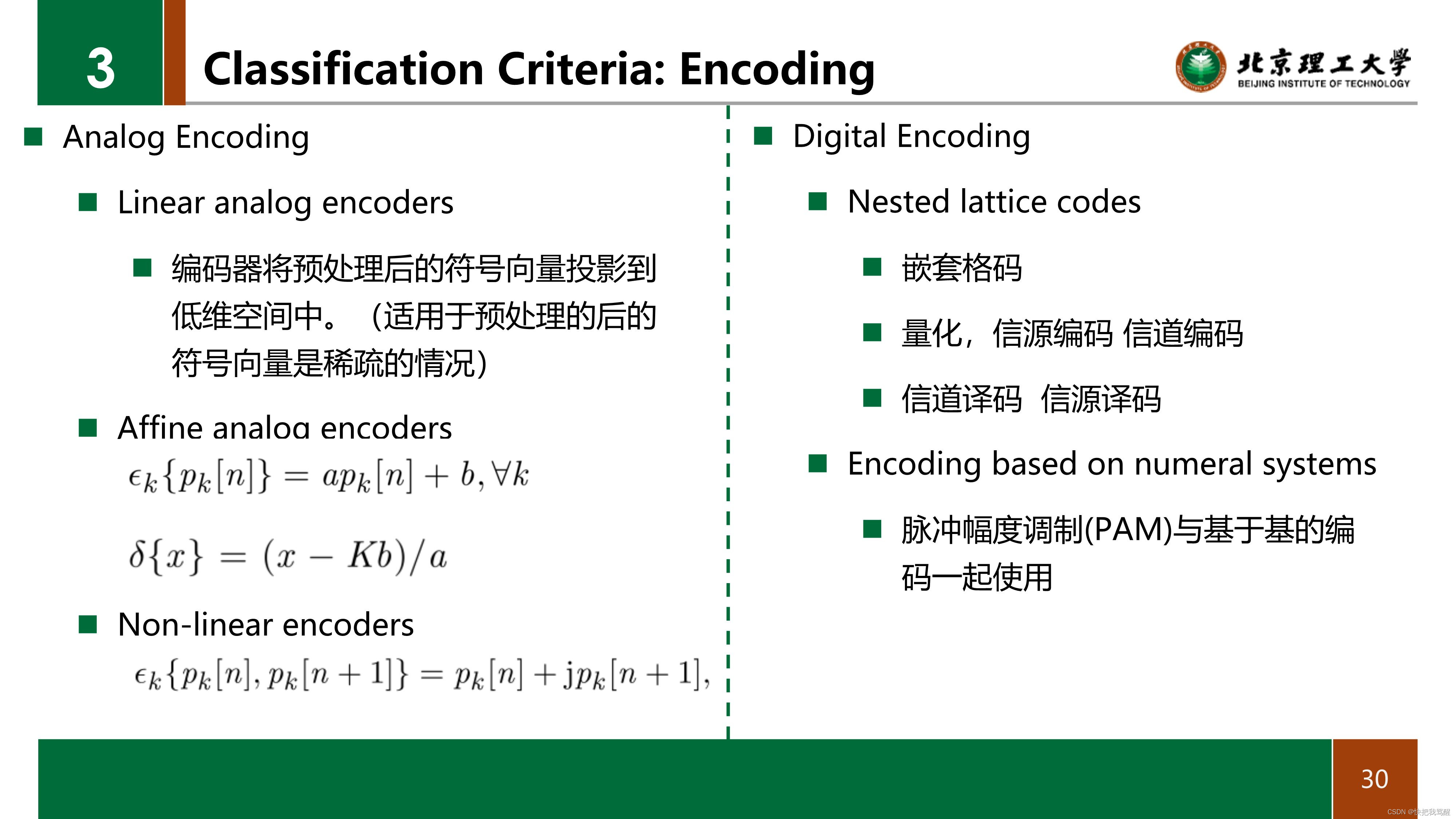
在这一类别中的分类特别关注:如何在以克服衰落信道为目标的线性编码器发生之前处理预处理函数的输出。 我们将这些方法分为模拟编码和数字编码。 当模拟编码处理连续值符号以实现所需的线图功能(通过模拟调制)时,数字编码使用某种形式的量化、压缩和/或信源信道编码用于相同的目标(通过数字调制)。
Analog encoding: 在文献中,大多数OAC方法利用可用的DOF而不需要特定的编码,只要在衰落信道下借助预编码器BK、K和解码器A保持可靠的叠加。然而,已经证明附加处理仍然有助于某些目标。

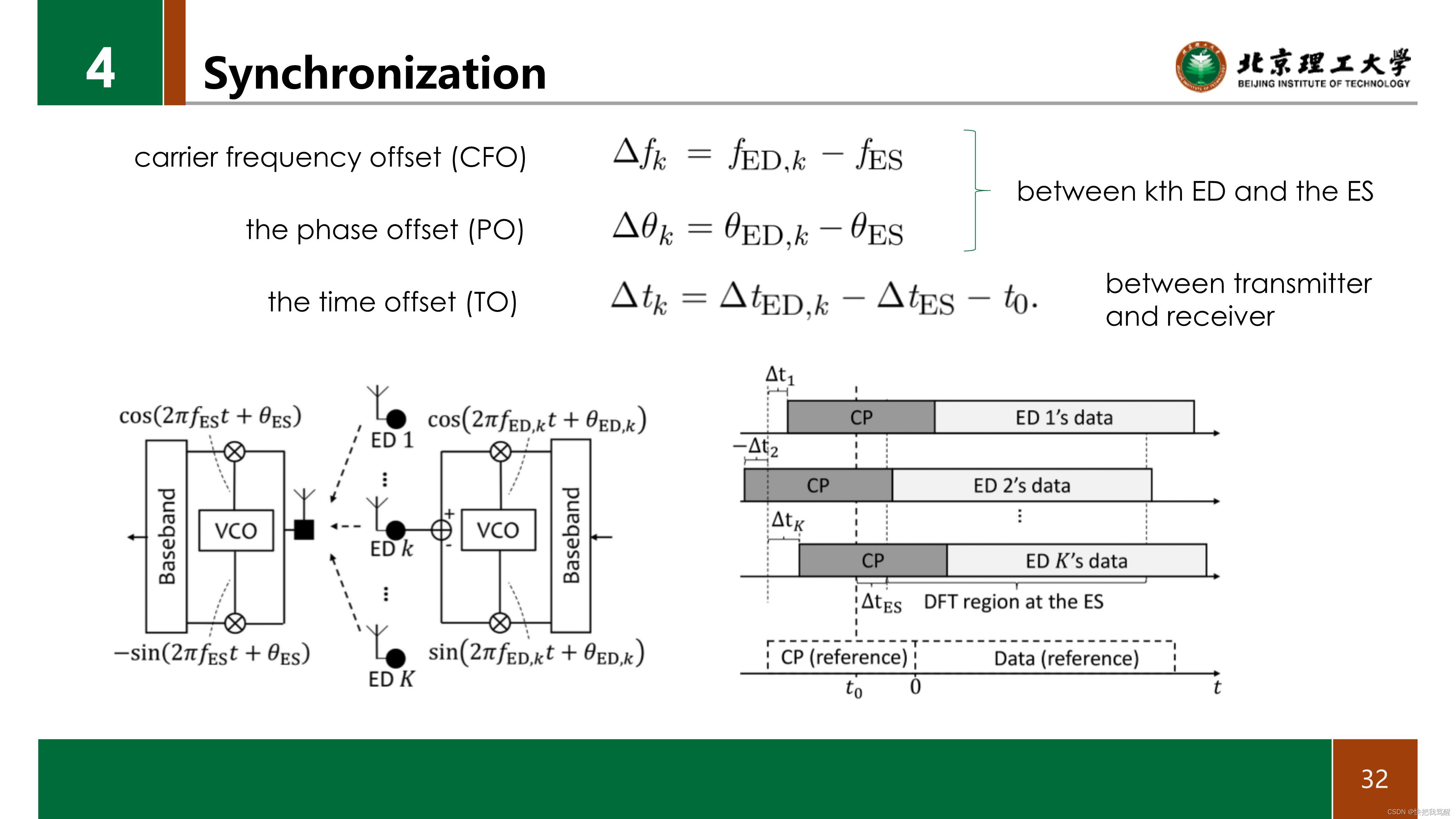
时间偏移(to): 让t0表示ES处的理想同步点。 假定在ES处的同步点和在ES位置处的第KED信号的到达时间瞬时分别偏离δTES秒和δTED,K秒。 因此,总TO可以表示为δtk=δted,k-δtes-t0。
设sk(t)∈C是要传输的第k个ED的基带信号。因此,从ES的角度来看,第k个ED的通带信号可以表示为

设sk(t)∈C是要传输的第k个ED的基带信号。因此,从ES的角度来看,第k个ED的通带信号可以表示为
1 EDS或ES的定时误差不仅在时间上转换信号,而且还引起额外的相位旋转。
2 CFO会导致相位误差累积,这种积累会随着时间的推移而增长。
3 根据时间偏移和路径延迟,CFO会导致额外的阶段旋转。
OFDM中
1 CFO的存在导致载波间干扰。
2 TO由于到达时间不完美或ES处的同步误差导致相位旋转随子载波下标缩放。
3 剩余的PO导致了与子载波索引无关的失真。
现在,假设OAC是基于OFDM的。对于t∈[0,Tsym),我们可以将第k个ED的基带信号表示为sk(t)= M−1 l=0 xk, e j2π l Tsym t,其中Tsym为符号持续时间,M为有源子载波数,xk为(7)中所示的传输符号。假设信道是理想信道,即P =1, ak, P =1, τk, P =0, k。同时,假设接收基带信号开始应用n点DFT的理想同步点在CP持续时间内,即在t0≤0时,如图4(b).5所示在同步损伤下,ES处第th子载波上接收到的符号可以表示为(42),如下一页底部所示,其中,ηFO,kΔfkTsym和ηTO,kΔtk/Tsym分别为第k ED的标准化CFO和TO,和DN(x)1 N N−1 N =0 j2π N N x = jπx N−1 N N sin(πx) sin(πx/N)是Dirichlet sinc核。由(42)可以看出,CFO的存在导致载波间干扰,而TO由于到达时间不完美或ES处的同步误差导致相位旋转随子载波指标缩放。


大多数研究仅考虑单小区,未考虑多小区的协作或利用多小区之间的干扰进行全局计算或消除信道大尺度衰落
在文献中,大多数关于OAC的论文考虑的要么是单细胞场景,要么是细胞之间没有合作的网络。另一方面,在处理大规模无线信道衰落时,通过一定的协调利用细胞间的干扰也会导致更全局的计算。
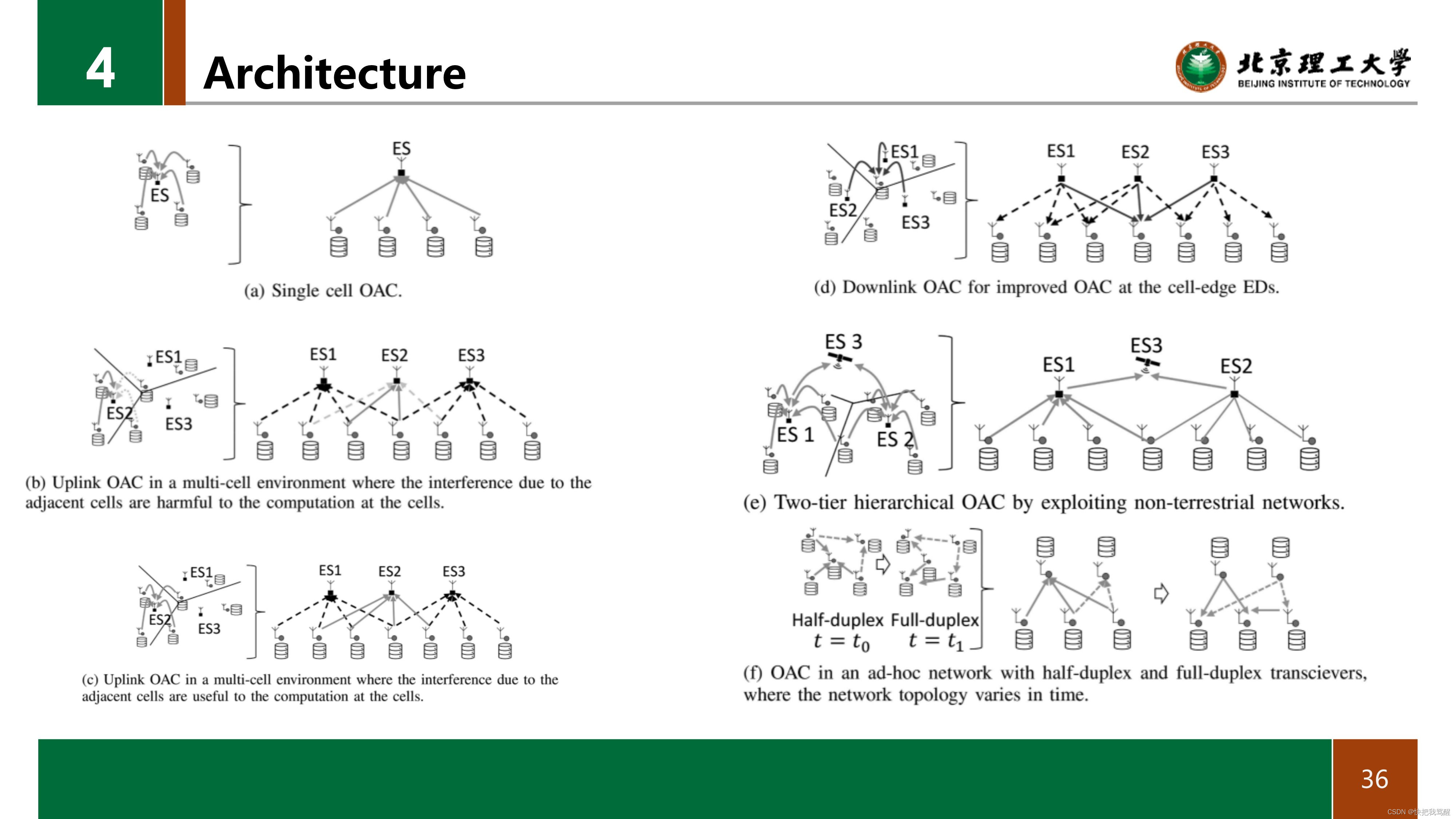
在图5中,我们说明了OAC的几个架构。与图5(a)中的单细胞场景相比,在多细胞场景中,相邻细胞的干扰可能被认为对OAC有害,如图5(b)所示,或用于图5©所示的计算。
与UL OAC类似,OAC也可以在DL中实现,如图5(d)所示。
在图5(e)中,我们展示了一种两层分层计算,中间ESs可以是基站,而最终融合节点可以是非地面网络中的卫星(以低地球轨道卫星为例,不需要分层计算,见[210])。
最后,图 5(f)示出了Ad-hoc网络中的OAC,例如,以在EDS之间实现关于功能输出的一致意见,其中网络拓扑可以随着时间而改变,并且EDS可以在考虑全双工收发器的情况下在向其他节点发送时执行OAC。




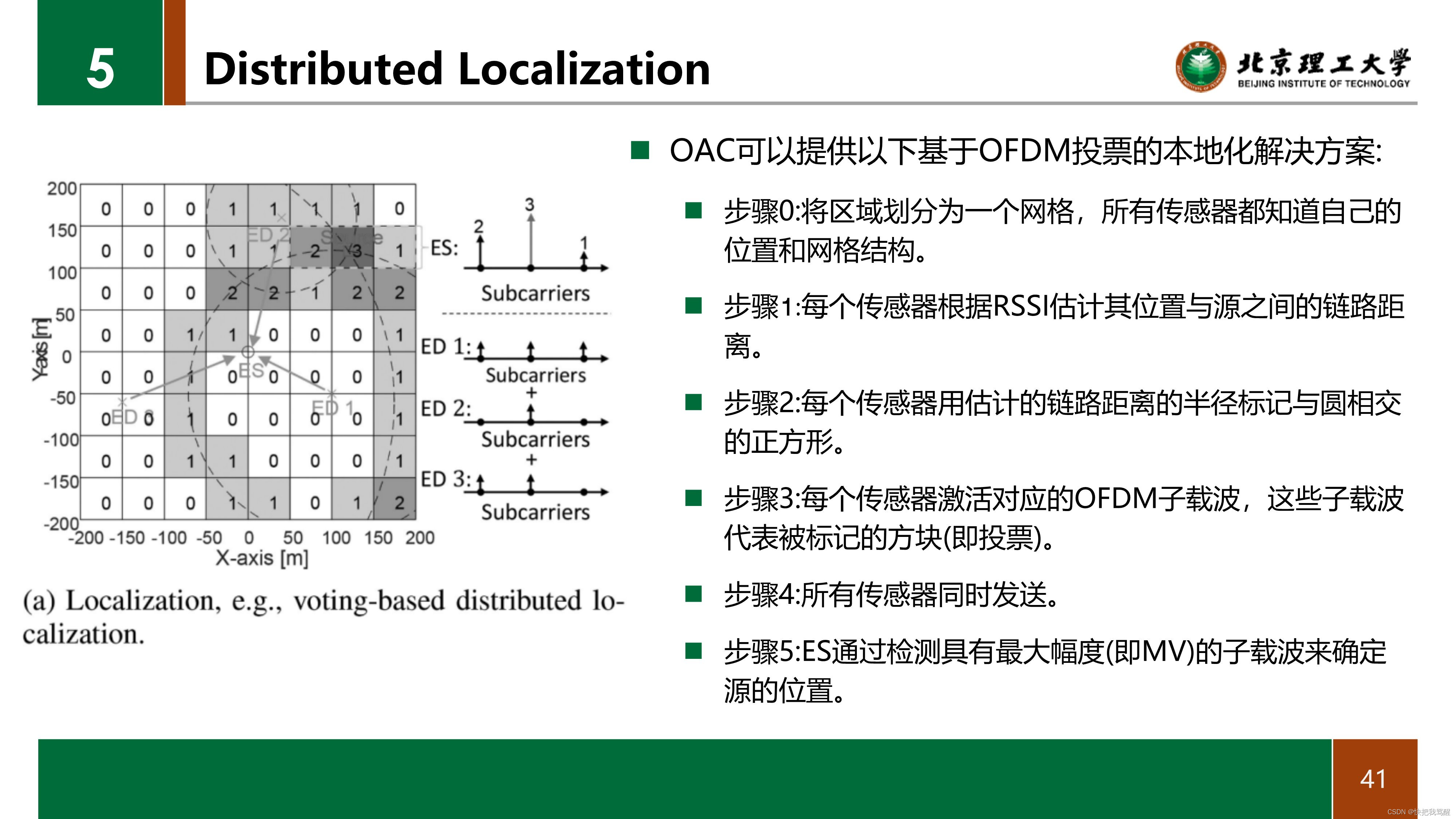
考虑这样一个场景,在一个区域中部署了许多传感器,以通过接收到的信号强度信息(RSSI),确定发射具有已知发射功率的信号的无线电源的位置。OAC可以提供以下基于OFDM投票的本地化解决方案[162]:
•步骤0:将区域划分为一个网格,所有传感器都知道自己的位置和网格结构。
•步骤1:每个传感器根据RSSI估计其位置与源之间的链路距离。
•步骤2:每个传感器用估计的链路距离的半径标记与圆相交的正方形。
•步骤3:每个传感器激活对应的OFDM子载波,这些子载波代表被标记的方块(即投票)。
•步骤4:所有传感器同时发送。
•步骤5:ES通过检测具有最大幅度(即MV)的子载波来确定源的位置。
这个过程不使用正交信道而是接收叠加的信号。

在控制理论中,动态对象是指当前状态随时间演化的状态空间模型。 它可以被建模为一组一阶线性差分方程,如x(t+1)=ax(t)+bu(t)+w(t),其中A和B是实值矩阵,u(t)是被控对象的控制行为,x(t)是被控对象的状态,w(t)是被控对象的噪声[12]。 动态对象的一个简单例子是摆,其中向量x(t)表示摆的角位置和速度[239]。 向量x(t)可能涉及大量空间分布的状态变量。 例如,对于化工厂,状态变量可能是温度、湿度和压力,而对于飞机,状态变量可能是大气压力、推力、阻力、速度和加速度。 在文献[12]中,考虑了一个用分布式传感器监测动态对象稳定性的场景。 其主要目标是通过尽可能快地获取当前状态,在有限的无线资源上稳定潜在不稳定的设备。 通过将多址信道引入动态对象相应的状态空间方程中,利用OAC支持大量传感器。我们还请读者参考[190],[239],[240]了解动态控制的进一步细节,其中主要目标是利用OAC恢复状态向量x(t)。 文献[241]将OAC应用于一般控制系统。 该方案考虑了传感器的发射功率,在发射功率受限的情况下尽量减少无线信道对控制系统的影响。 文献[101]提出了一种基于OAC的分布式一致性控制方法。 OAC用于计算车辆的平均位置,用于计算每辆车的加速器以稳定排。 对于OAC,作者提出在发射机处将参数(车辆位置的缩放版本)与信道实部的符号相乘,以便在接收机处获得相干加法。 只有实部分符号用于计算。 在文献[218]中,用OAC研究了图神经网络在多机器人群体中的实现
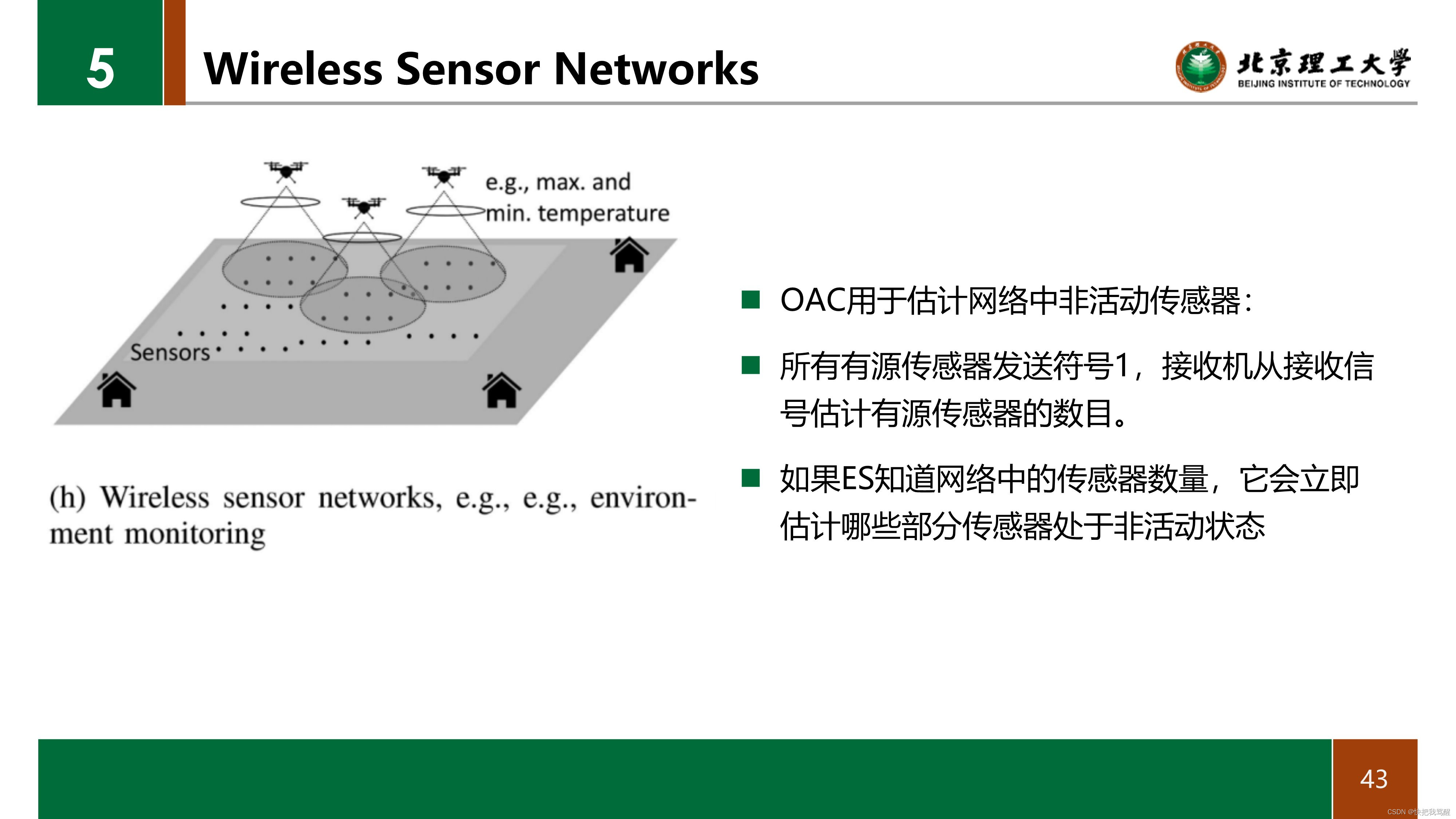
在[37]中,OAC用于估计网络中非活动传感器的部分。 对于该应用,所有有源传感器发送符号1,接收机从接收信号估计有源传感器的数目。 如果ES知道网络中的传感器数量,它会立即估计哪些部分传感器处于非活动状态。 在[37]中可以找到一个OAC的例子,用于计算由250个传感器测量的环境监测温度的算术平均值。文献[63]中给出了OAC在无线传感器网络领域的其他应用,如计算读数满足某一阈值的传感器的数量、测量温度的方差或与观测测量的最佳线性拟合,即回归。 在文献[92]中,基于环境感知和无线电地图构建的动机,研究了分布式网络上基于专家乘积的高斯过程回归,其中所研究的OAC方案是基于ZF预编码器和PC机的。 在[119]中,作者考虑了一个分布式传感应用,其中所有传感器观察数据的线性组合。 在[90],[242]中,利用无人机的机动性来改善ZF基OAC的功率对准。 通过对簇内信号进行协调,同时减少簇间干扰,对簇内调度、关联和无人机轨迹进行了联合优化。 文[96]也研究了基于无人机的聚合。 类似地,在[243]中研究了考虑多时隙OAC的无人机轨迹优化问题,在[87]中,作者考虑了基于OAC的远程监控应用中,在时变环境下,除了MSE之外,还考虑了聚合数据的新鲜度。 在文献[164]中,考虑了OAC通过低功耗广域网构建地理热量分布,以探测森林火灾
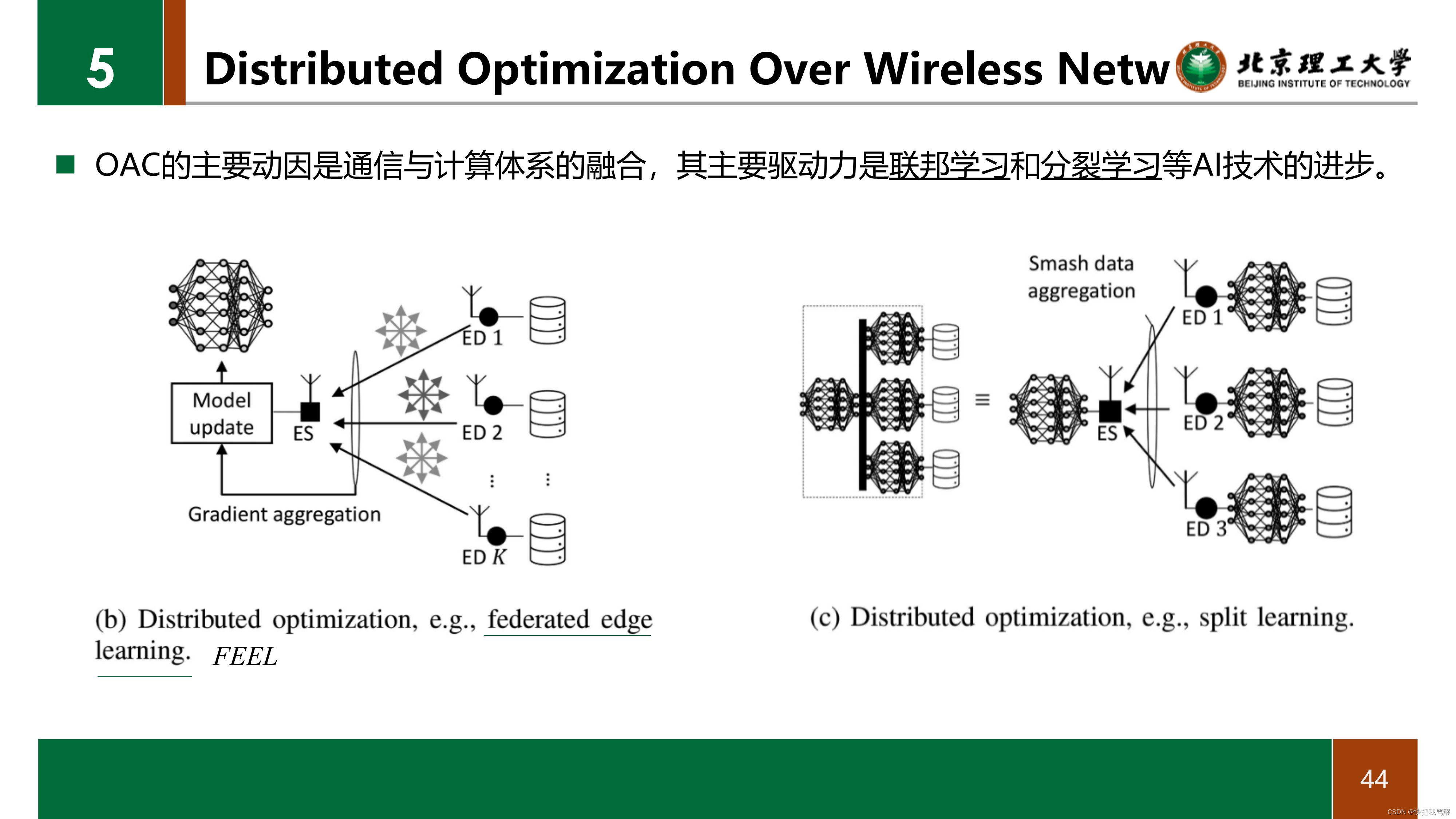
FL [26] is one of the most studied distributed learning frameworks. The task of model training is distributed across multiple EDs and data uploading is avoided to promote the user-privacy. Instead of data samples, EDs share a large number of local stochastic gradients or local model parameters with an ES for aggregation. 联邦学习是很有名的分布式学习框架。模型训练的任务分布在多个边缘设备。从而避免了用户数据上传来提高保密性。EDs向ES共享大量的局部随机梯度或局部模型参数,而不是数据样本。
federated edge learning (FEEL), i.e., implementation of federated learning (FL) [26] over a wireless network, 在联邦边缘学习中,通过OAC将通信与计算结合,可以极大加快训练速度。例如用OAC所有ED同时传输,上传局部梯度的加权平均值,其开销仅相当于单个ED的开销。
FEEL中UL或者DL传输的信息,由于其特性,在UL中,即使传输其sign,也能收敛。DL中,OAC广播聚合后的梯度对位于小区边缘的Eds的聚合有益。
SL(分裂学习):在EDs和ES上分裂神经网络, 这样EDS可以保护其局部数据集的私密性,同时减少ED方面的计算负担。EDS将网络训练到一个特定的层,称为剪切层,并将剪切层的输出,即smashed数据,与标签一起发送给ES。ES从聚合EDs的smash数据的层(即聚合层)开始完成前进步骤的其余部分。然后,ES开始将梯度从ES的神经网络的最后一层向第一层反向传播,并将关于smash数据的梯度发送给EDS。 前向和后向传播一直持续到网络收敛。与FL相比SL的优点是具有更少的层数。
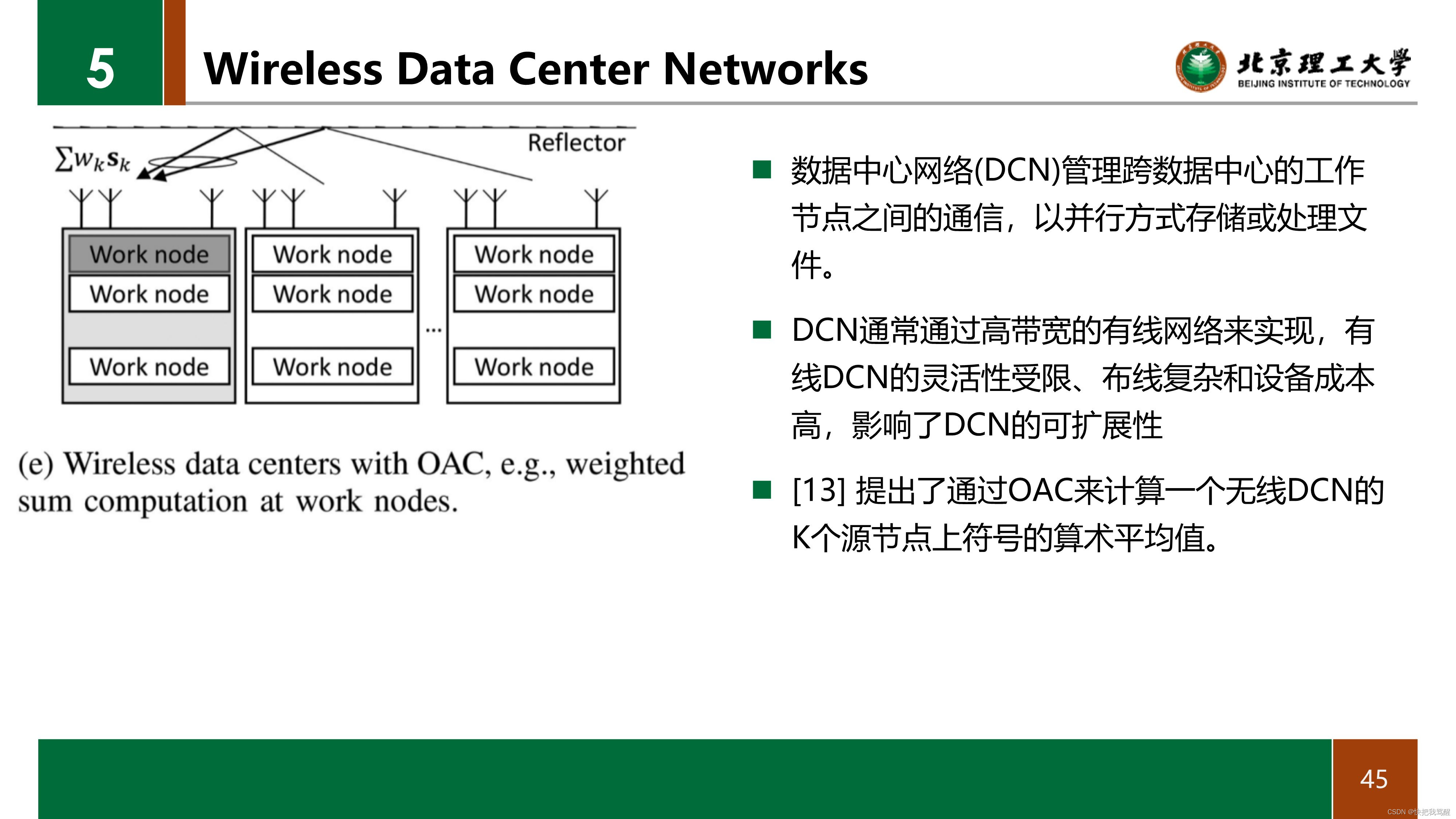
数据中心网络(DCN)管理跨数据中心的工作节点之间的通信,以并行方式存储或处理文件。 它通常通过高带宽的有线网络来实现。 另一方面,有线DCN的灵活性有限、布线复杂和设备成本高,影响了DCNS的可扩展性。 为了解决这些问题,在文献[13]中,提出了OAC来计算一个无线DCN的K个源节点上符号的算术平均值。
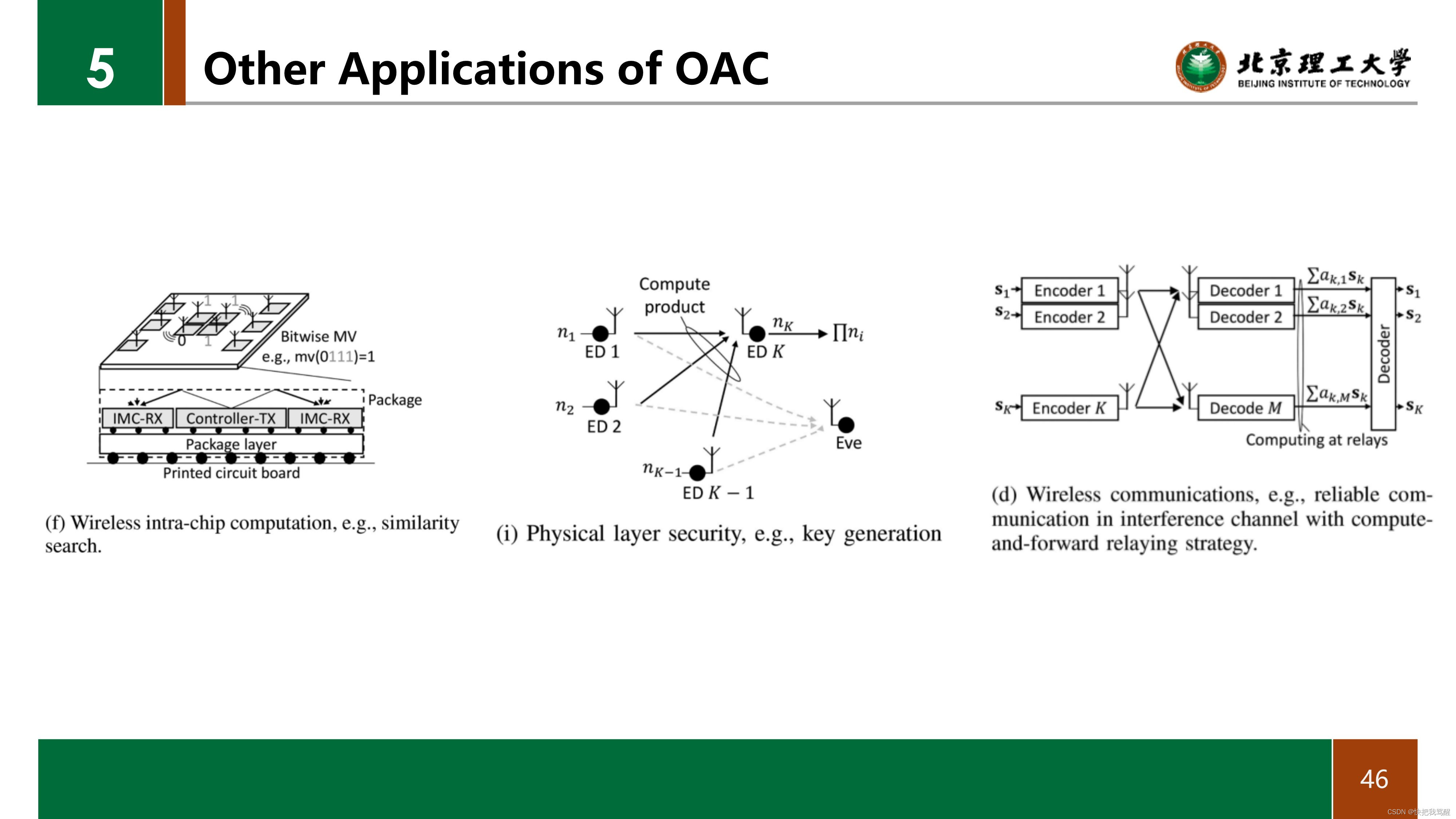
除了上述。还介绍了无线片内计算。
物理层安全与秘钥生成(OAC乘以高斯质数来计算可用于任何加密过程或生成密钥的秘密密钥, 具体来说每个节点被分配一个数字,所有EDs通过顺序改变目的节点来计算OAC的乘积).
计算,转发,中继策略:当信道上发生冲突时,非基于调度的信道接入协议,要求相关设备使用退避机制再次访问信道,会造成速率减小。
此时为了解决这个问题,可以在节点处利用冲突,并且节点将消息的线性组合连同用于解码的相应系数一起转发给基站。










栈)












)
)

 认识Vue)
