392. 判断子序列 - 力扣（LeetCode）
给定字符串 s 和 t ，判断 s 是否为 t 的子序列。字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。
进阶：如果有大量输入的 S，称作 S1, S2, ... , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？
示例 1：
输入：s = "abc", t = "ahbgdc" 输出：true
示例 2：
输入：s = "axc", t = "ahbgdc" 输出：false
>>思路和分析
- 只需要计算删除的情况
（一）动规五部曲
1.确定dp数组（dp table）以及下标的含义
- dp[i][j] : 表示以下标 i-1 为结尾的字符串 s ，和以下标 j-1 为结尾的字符串 t ，相同子序列的长度为dp[i][j]
2.确定递推公式
- ① if(s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] + 1
- ② if(s[i-1] != t[j-1]) dp[i][j] = dp[i][j-1]
如果 s[i-1] == t[j-1]，说明当前在遍历串t 时找到了一个字符和 串s的字符 匹配，那么相同子序列长度就在dp[i-1][j-1]的基础上加1
如果 s[i-1] != t[j-1]，说明当前在遍历串t 时这个字符和 串s的字符 不匹配，此时相当于 t 要删除元素，若 t 把当前元素t[j-1]删除，那么 dp[i][j] 的数值就是看 s[i-1] 与 t[j-2] 的比较结果，即：dp[i][j] = dp[i][j-1];
3.dp数组初始化
- 从递推公式可以看出 dp[i][j] 都是依赖于 dp[i-1][j-1] 和 dp[i][j-1] ，所以 dp[0][0] 和 dp[i][0] 是一定要初始化的
vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
4.确定遍历顺序
- 从递推式可以看出 dp[i][j] 依赖于 dp[i-1][j-1] 和 dp[i][j-1]，遍历顺序应该是从上到下，从左到右
5.举例推导dp数组
- dp[i][j] : 表示以下标 i-1 为结尾的字符串 s ，和以下标 j-1 为结尾的字符串 t ，相同子序列的长度为dp[i][j]
那么dp[s.size()][t.size()] = 3，而s.size() = 3，故 s 是 t 的子序列，返回 true
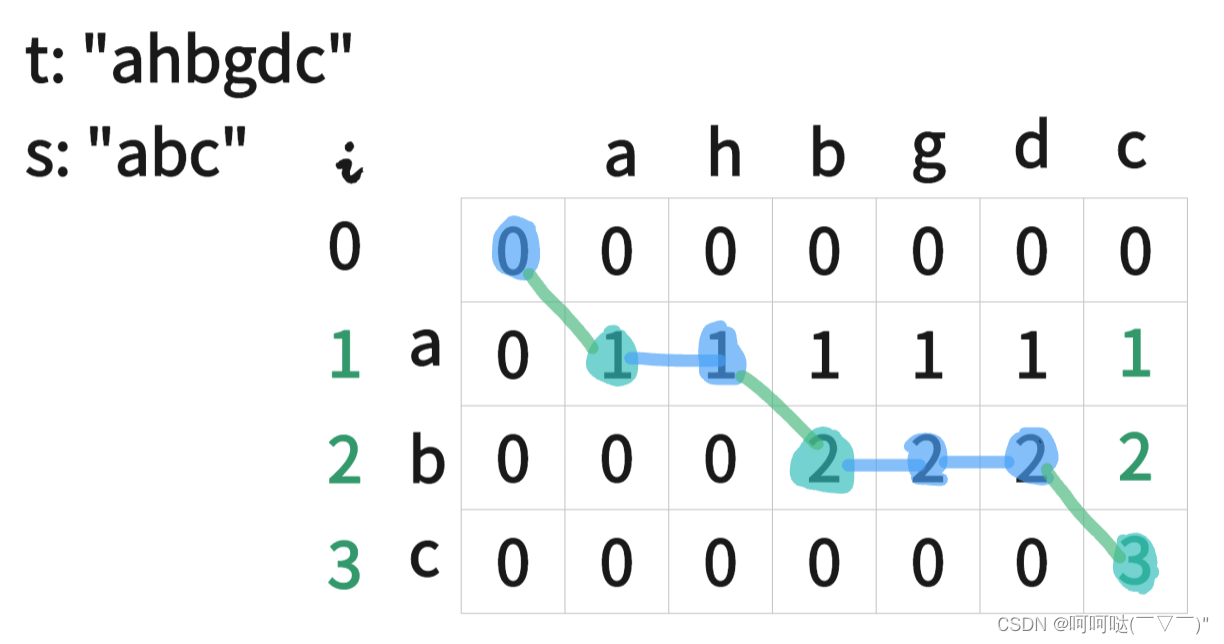
注：观察此表格我们可以发现，当串s在串t中寻找某一个字符成功时，每一行的最后一个数值都等于当前的 i 值。所以下文代码中有一句 if(dp[i][t.size()] !=i) return false; 说明 串s 中的某一个字符在 串t 中实在无法找不到了，就直接返回false
（1）动态规划 二维dp
class Solution {
public: // 动态规划 二维dpbool isSubsequence(string s, string t) {vector<vector<int>> dp(s.size()+1,vector<int>(t.size()+1,0));for(int i=1;i<=s.size();i++) {for(int j=1;j<=t.size();j++) {if(s[i-1] == t[j-1]) {dp[i][j] = dp[i-1][j-1] + 1;}else dp[i][j] = dp[i][j-1];}if(dp[i][t.size()] !=i) return false;}return dp[s.size()][t.size()] == s.size();}
};- 时间复杂度：O(n × m)
- 空间复杂度：O(n × m)
（2）二维dp 优化空间
class Solution {
public:// 二维dp 优化空间复杂度bool isSubsequence(string s, string t) {vector<vector<int>> dp(2,vector<int>(t.size()+1,0));for(int i=1;i<=s.size();i++) {for(int j=1;j<=t.size();j++) {if(s[i-1] == t[j-1]) dp[i % 2][j] = dp[(i-1)%2][j-1] + 1;else dp[i % 2][j] = dp[i % 2][j-1];}if(dp[i%2][t.size()] !=i) return false;}return dp[s.size() % 2][t.size()] == s.size();}
};- 时间复杂度：O(n × m)
- 空间复杂度：O(m)
（3）一维dp 优化空间
class Solution {
public: // 一维dp 滚动数组 优化空间复杂度bool isSubsequence(string s, string t) {vector<int> dp(t.size()+1,0);for(int i=1;i<=s.size();i++) {int pre = dp[0];for(int j=1;j<=t.size();j++) {int tmp = dp[j];if(s[i-1] == t[j-1]) dp[j] = pre + 1;else dp[j] = dp[j-1];pre = tmp;}if(dp[t.size()] !=i) return false;}return dp[t.size()] == s.size();}
};- 时间复杂度：O(n × m)
- 空间复杂度：O(m)
- 我思考之后发现内层for循环里的 j 的起始位置可以改一下
class Solution {
public: bool isSubsequence(string s, string t) {vector<vector<int>> dp(s.size()+1,vector<int>(t.size()+1,0));int tmp=1;for(int i=1;i<=s.size();i++) {bool flag = 0;for(int j=tmp;j<=t.size();j++) {if(s[i-1] == t[j-1]) {dp[i][j] = dp[i-1][j-1] + 1;if(!flag) tmp=j;flag=1;}else dp[i][j] = dp[i][j-1];}if(dp[i][t.size()] !=i) return false;}return dp[s.size()][t.size()] == s.size();}（二）双指针
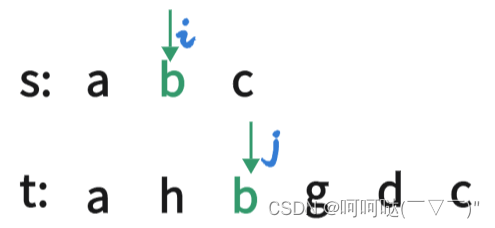
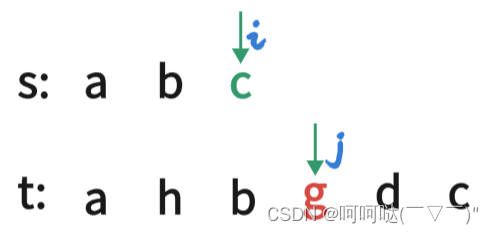
（1）while循环写法
class Solution {
public:bool isSubsequence(string s,string t) {int i=0,j=0;while(i<s.size() && j<t.size()) {if(s[i] == t[j]) {i++;j++;}else j++; }if(i == s.size()) return true;return false;}
};（2）for循环写法
class Solution {
public:bool isSubsequence(string s,string t) {if(s.size()==0) return true;int i=0;for(auto c:t) {if(s[i] == c) {i+=1;if(i == s.size()) return true;}}return false;}
};参考和推荐文章、视频：
代码随想录 (programmercarl.com)
https://www.programmercarl.com/0392.%E5%88%A4%E6%96%AD%E5%AD%90%E5%BA%8F%E5%88%97.html#%E6%80%9D%E8%B7%AF动态规划，用相似思路解决复杂问题 | LeetCode：392.判断子序列_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1tv4y1B7ym/?spm_id_from=pageDriver&vd_source=a934d7fc6f47698a29dac90a922ba5a3来自代码随想录课堂视频截图：
- 我写的另一个版本（串 s 用双指针，串 t 也用双指针）：
class Solution {
public:bool isSubsequence(string s,string t) {int sl=0,sr=s.size()-1;int tl=0,tr=t.size()-1;int count = 0;if(s.size()==0) return true;while(sl<=sr && tl <= tr) {if(s[sl] == t[tl]) {sl++;tl++;count++;}else tl++;if(tl < tr && s[sr] == t[tr]) {sr--;tr--;count++;}else tr--;}if(s.size() == count) return true;return false;}
};把串s看作是一个装着 串s 字符的栈 ：
class Solution {
public:bool isSubsequence(string s,string t) {if(s.empty()) return true;for(int i=t.size()-1;i>=0;i--) {if(t[i] == s.back()) {s.pop_back();if(s.empty()) return true;};}return false;}
};
