❓ 289. 生命游戏

难度：中等

根据 百度百科 ， 生命游戏 ，简称为 生命 ，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

1. 如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
2. 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
3. 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
4. 如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

示例 1：

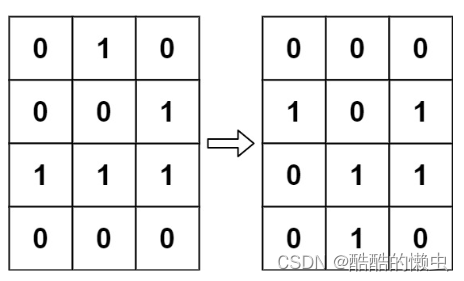
输入：board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出：[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

示例 2：

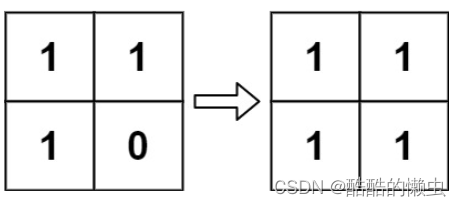
输入：board = [[1,1],[1,0]]
输出：[[1,1],[1,1]]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 25
• board[i][j] 为 0 或 1

进阶：

• 你可以使用原地算法解决本题吗？请注意，面板上所有格子需要同时被更新：你不能先更新某些格子，然后使用它们的更新后的值再更新其他格子。
• 本题中，我们使用二维数组来表示面板。原则上，面板是无限的，但当活细胞侵占了面板边界时会造成问题。你将如何解决这些问题？

💡思路：(位运算，原地解决)

由题意细胞的出生和死亡是同时发生的，所以当前时刻的所有状态都要被保存，在不使用额外空间的情况下，可以使用原数组进行保存，原数组 只是用了一位来记录细胞状态，所以我们可以使用 高一位 来记录下一刻所有细胞的状态。

规则总结：p 细胞周围8个位置(中的不越界部分)存在

• 1、小于2个或多余3个活细胞1时，p下一状态必然是死细胞 0。
• 2、当 p 周围有2个时，p不变，周围有3个 1 时，若 p 是 0 则复活变为 1，若 p是 1 则不变。

位运算状态存储 ：

• 原数组值仅有 1 或 0 ，那么可以用二进制高一位存储其变更后的状态；
• 每个点 p 在作为周边位置参与统计 1 时使用 最低位 数字，p 作为中心点时根据统计结果得到的下一步状态存储在最高位(第二位)。

🍁代码：(C++、Java)

C++

class Solution {
public:int dir[8][2] = {{-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1}};void gameOfLife(vector<vector<int>>& board) {int m = board.size(), n = board[0].size();for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){int cnt = 0;for(int k = 0; k < 8; ++k){int row = i + dir[k][0], col = j + dir[k][1];if(row >= 0 && row < m && col >= 0 && col < n && (board[row][col] & 1) == 1){++cnt;}}if(cnt == 3){board[i][j] |= (1 << 1);}else if(cnt == 2){board[i][j] |= (board[i][j] << 1);}}}for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){board[i][j] >>= 1;}}}
};

Java

class Solution {int [][] dir = {{-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1}};public void gameOfLife(int[][] board) {int m = board.length, n = board[0].length;for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){int cnt = 0;for(int k = 0; k < 8; ++k){int row = i + dir[k][0], col = j + dir[k][1];if(row >= 0 && row < m && col >= 0 && col < n && (board[row][col] & 1) == 1){++cnt;}}if(cnt == 3){board[i][j] |= (1 << 1);}else if(cnt == 2){board[i][j] |= (board[i][j] << 1);}}}for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){board[i][j] >>= 1;}}}
}

🚀 运行结果：

🕔 复杂度分析：

• 时间复杂度：$O(mn)$，其中m， n 分别为 board 的行数和列数。
• 空间复杂度：$O(1)$，除原数组外只需要常数的空间存放若干变量。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我LeetCode主页 / CSDN—力扣专栏，每日更新！

注： 如有不足，欢迎指正！