基于深度优先搜索的无向图遍历

使用深度优先搜索遍历无向图，将无向图用邻接表存储：

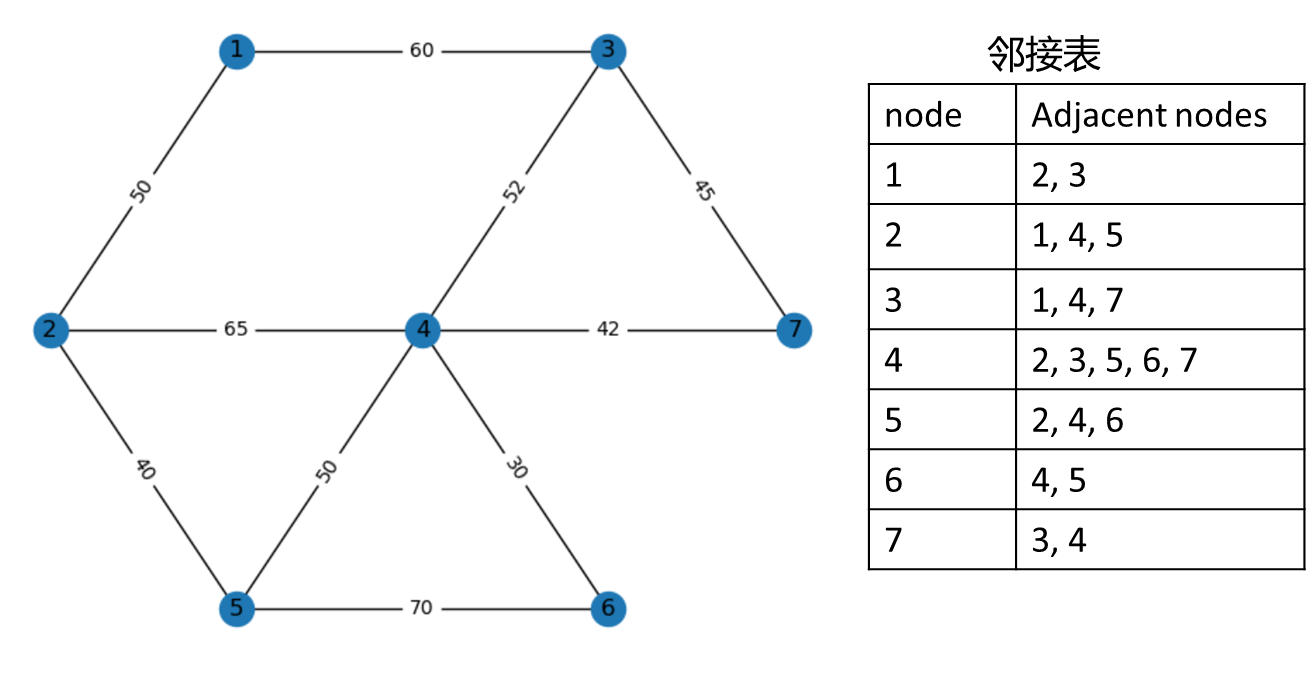
算法流程图

1. 初始化起点 source，当前节点v为起点，终点 target，路径path为空，路径集合 paths 为空
2. 将当前节点v添加到 path 中
3. 判断当前节点v是否为终点，是转step4，否转step5
4. 保存 path 至 paths 中，转step7
5. 获取当前节点的所有邻接点，用集合N表示
6. 遍历N，若 N_i 不在 path 中，令v=N_i ，转step2；若N_i 在path 中，i +=1。
7. 删除 path 中最后一个节点,令v=path中最后一个节点，转step5
8. 以上步骤遍历了所有每一个点的邻接点，算法结束，输出起点到终点的所有路径paths

Python实现

from typing import Listdef dfs(adjacent_list, source, target):""":param adjacent_list: 邻接表:param source: 起点:param target: 终点:return: 起点-终点的所有路径"""def dfs_helper(adjacent_list, source, current_node, target):path.append(current_node)  # 压栈if current_node == target:paths.append(path.copy())else:neighbors = adjacent_list[current_node]for neighbor in neighbors:if neighbor not in path:dfs_helper(adjacent_list, source, neighbor, target)path.pop()  # 弹栈paths = []path = []dfs_helper(adjacent_list, source, source, target)return pathsif __name__ == "__main__":# 邻接表adjacent_list = {1: [2, 3],2: [1, 4, 5],3: [1, 4, 7],4: [2, 3, 5, 6, 7],5: [2, 4, 6],6: [4, 5],7: [3, 4]}# 深搜paths: List[List] = dfs(adjacent_list, 1, 6)[print(path) for path in paths]

Java实现

package org.example;import java.util.*;public class DepthFirstSearch {//    List<Integer> path = new ArrayList<>();Stack<Integer> path = new Stack<>();List<List<Integer>> paths = new ArrayList<>();void dfs(Map<Integer, List<Integer>> adjacent_list, int source, int current_node, int target) {path.push(current_node);if (current_node == target) {paths.add(new ArrayList<>(path));path.remove(path.size() - 1);} else {List<Integer> neighbors = adjacent_list.get(current_node);for (Integer neighbor : neighbors) {if (!path.contains(neighbor)) {dfs(adjacent_list, source, neighbor, target);}}path.pop();}}public static void main(String[] args) {Map<Integer, List<Integer>> adjacent_list = new HashMap<>();adjacent_list.put(1, Arrays.asList(2, 3));adjacent_list.put(2, Arrays.asList(1, 4, 5));adjacent_list.put(3, Arrays.asList(1, 4, 7));adjacent_list.put(4, Arrays.asList(2, 3, 5, 6, 7));adjacent_list.put(5, Arrays.asList(2, 4, 6));adjacent_list.put(6, Arrays.asList(4, 5));adjacent_list.put(7, Arrays.asList(3, 4));System.out.println(adjacent_list);DepthFirstSearch dfs = new DepthFirstSearch();dfs.dfs(adjacent_list, 1, 1, 6);for (List<Integer> path : dfs.paths) {System.out.println(path);}}
}

基于深度优先搜索的有向图遍历

和无向图遍历一样，建立邻接矩阵即可。

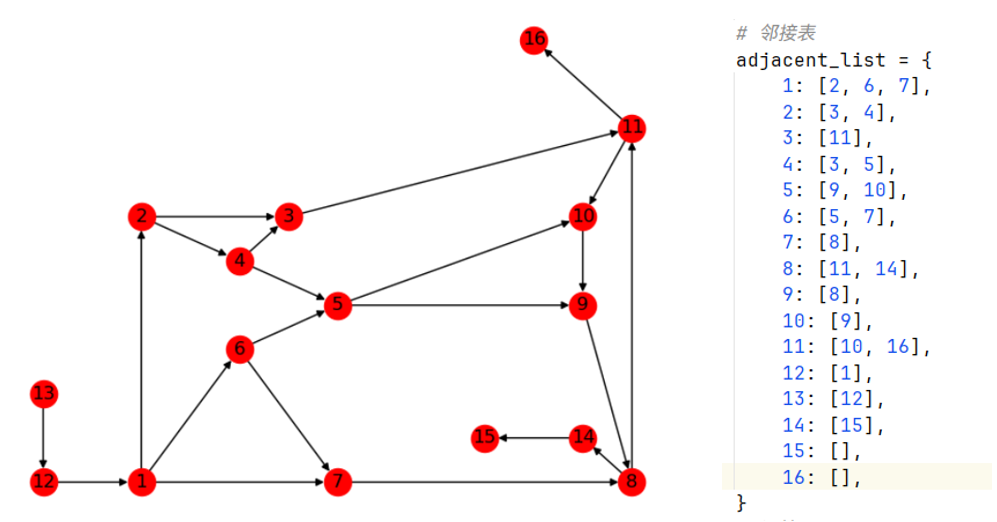
Python实现

from typing import List, Tuple, Any, Dict
import networkx
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from typing import Listdef paint_topological_graph(nodes,edges: List[Tuple],coordinates: Dict[Any, Tuple] = None,directed=False):print(nodes)print(edges)print(coordinates)graph = networkx.DiGraph() if directed else networkx.Graph()  # 全连通 有向图graph.add_nodes_from(nodes)graph.add_edges_from(edges)networkx.draw(graph, pos=coordinates, with_labels=True, node_color='red', )plt.show()print(networkx.has_path(graph, 1, 12))return graphdef dfs(adjacent_list, source, target):""":param adjacent_list: 邻接表:param source: 起点:param target: 终点:return: 起点-终点的所有路径"""def dfs_helper(adjacent_list, source, current_node, target):path.append(current_node)if current_node == target:paths.append(path.copy())path.pop()else:neighbors = adjacent_list[current_node]for neighbor in neighbors:if neighbor not in path:dfs_helper(adjacent_list, source, neighbor, target)path.pop()paths = []path = []dfs_helper(adjacent_list, source, source, target)return pathsif __name__ == "__main__":# 点坐标node_coord = {1: (1, 0), 2: (1, 3), 3: (2.5, 3), 4: (2, 2.5), 5: (3, 2), 6: (2, 1.5), 7: (3, 0), 8: (6, 0), 9: (5.5, 2),10: (5.5, 3), 11: (6, 4), 12: (0, 0), 13: (0, 1), 14: (5.5, 0.5), 15: (4.5, 0.5), 16: (5, 5),}edges = [(13, 12), (1, 2), (2, 4), (2, 3), (4, 3), (4, 5), (1, 6), (1, 7), (6, 7), (6, 5), (7, 8), (5, 9), (5, 10),(3, 11), (11, 10), (9, 8), (10, 9), (8, 11), (14, 15), (8, 14), (12, 1), (11, 16),]# 画图paint_topological_graph(nodes=np.arange(1, 17, 1),edges=edges,directed=True,coordinates=node_coord)# 邻接表adjacent_list = {1: [2, 6, 7],2: [3, 4],3: [11],4: [3, 5],5: [9, 10],6: [5, 7],7: [8],8: [11, 14],9: [8],10: [9],11: [10, 16],12: [1],13: [12],14: [15],15: [],16: [],}# 深搜paths: List[List] = dfs(adjacent_list, 1, 11)[print(path) for path in paths]