4.23 推导
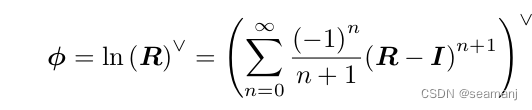
f ( x ) f(x) f(x)在点a处的泰勒展开
f ( x ) = ∑ n = 0 ∞ f ( n ) a n ! ( x − a ) n f(x) = \sum_{n=0}^\infty \frac{f^{(n)}a}{n!}(x-a)^n f(x)=∑n=0∞n!f(n)a(x−a)n
l n x lnx lnx的n阶导数
l n ( n ) x = ( − 1 ) n − 1 ( n − 1 ) ! x n ln^{(n)}x = \frac{(-1)^{n-1}(n-1)!}{x^n} ln(n)x=xn(−1)n−1(n−1)!
l n ( R ) ln(R) ln(R)在 I I I处展开
l n ( R ) = ∑ n = 0 ∞ l n ( n ) I ( R − I ) n n ! = ∑ n = 1 ∞ l n ( n ) I ( R − I ) n n ! = ∑ n = 1 ∞ ( − 1 ) n − 1 ( R − I ) n n = ∑ n = 0 ∞ ( − 1 ) n ( R − I ) n + 1 n + 1 \begin{aligned} ln(R) & =\sum_{n=0}^\infty\frac{ln^{(n)}I(R-I)^n}{n!} \\ & = \sum_{n=1}^\infty\frac{ln^{(n)}I(R-I)^n}{n!} \\ & = \sum_{n=1}^\infty\frac{(-1)^{n-1}(R-I)^n}{n}\\ & = \sum_{n=0}^\infty\frac{(-1)^{n}(R-I)^{n+1}}{n+1} \end{aligned} ln(R)=n=0∑∞n!ln(n)I(R−I)n=n=1∑∞n!ln(n)I(R−I)n=n=1∑∞n(−1)n−1(R−I)n=n=0∑∞n+1(−1)n(R−I)n+1
4.24 推导
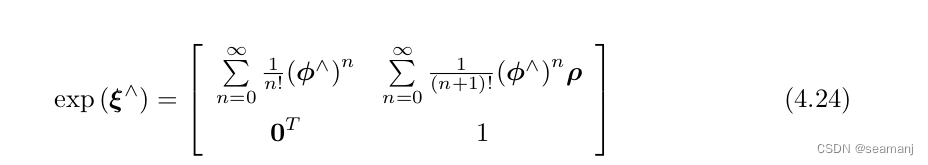
ξ ∧ = [ ϕ ∧ ρ 0 T 0 ] \begin{aligned} \xi ^ \wedge = \begin{bmatrix} \phi ^ \wedge & \rho\\ 0^T & 0 \end{bmatrix} \end{aligned} ξ∧=[ϕ∧0Tρ0]
e x p ( ξ ∧ ) = ∑ n = 0 ∞ 1 n ! [ ϕ ∧ ρ 0 T 0 ] n = I + ∑ n = 1 ∞ 1 n ! [ ϕ ∧ ρ 0 T 0 ] n = [ I 0 0 T 1 ] + ∑ n = 1 ∞ 1 n ! [ ( ϕ ∧ ) n ( ϕ ∧ ) n − 1 ρ 0 T 0 ] = [ I + ∑ n = 1 ∞ 1 n ! ( ϕ ∧ ) n ∑ n = 1 ∞ 1 n ! ( ϕ ∧ ) n − 1 ρ 0 T 1 ] = [ ∑ n = 0 ∞ 1 n ! ( ϕ ∧ ) n ∑ n = 0 ∞ 1 ( n + 1 ) ! ( ϕ ∧ ) n ρ 0 T 1 ] \begin{aligned} exp(\xi ^ \wedge) &= \sum_{n=0}^{\infty}\frac{1}{n!}\begin{bmatrix} \phi ^ \wedge & \rho\\ 0^T & 0 \end{bmatrix}^n=I + \sum_{n=1}^{\infty}\frac{1}{n!}\begin{bmatrix} \phi ^ \wedge & \rho\\ 0^T & 0 \end{bmatrix}^n = \begin{bmatrix}I & 0\\ 0^T & 1 \end{bmatrix} + \sum_{n=1}^{\infty}\frac{1}{n!}\begin{bmatrix} (\phi ^ \wedge)^n & (\phi ^ \wedge)^{n-1}\rho\\ 0^T & 0 \end{bmatrix} \\ &=\begin{bmatrix}I + \sum_{n=1}^{\infty}\frac{1}{n!}(\phi ^ \wedge)^n & \sum_{n=1}^{\infty}\frac{1}{n!}(\phi ^ \wedge)^{n-1}\rho\\ 0^T & 1 \end{bmatrix} \\ &=\begin{bmatrix}\sum_{n=0}^{\infty}\frac{1}{n!}(\phi ^ \wedge)^n & \sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi ^ \wedge)^{n}\rho\\ 0^T & 1 \end{bmatrix} \end{aligned} exp(ξ∧)=n=0∑∞n!1[ϕ∧0Tρ0]n=I+n=1∑∞n!1[ϕ∧0Tρ0]n=[I0T01]+n=1∑∞n!1[(ϕ∧)n0T(ϕ∧)n−1ρ0]=[I+∑n=1∞n!1(ϕ∧)n0T∑n=1∞n!1(ϕ∧)n−1ρ1]=[∑n=0∞n!1(ϕ∧)n0T∑n=0∞(n+1)!1(ϕ∧)nρ1]




实现一个简单的聊天)
】14 - Passthrough配置文件 /mnt/vm/images/linux-la.config 内容分析)





)





进行换行展示)

