文章目录
- 1、导数的概念
- 1.1、引例
- 1.1.1、变速直线运动瞬时速度
- 1.1.2、曲线的切线
- 1.2、导数的定义
- 1.3、证明常用导数
- 1.4、导数的几何意义
- 1.5、可导与连续的关系
- 2、函数的求导法则
- 2.1、函数的和、差、积、商的求导法则
- 2.2、反函数的求导法则
- 2.3、复合函数的求导法则
- 2.4、基本初等函数的导数公式
- 3、高阶导数
- 3.1、高阶导数的公式
- 4、隐函数和参数方程确定的函数的导数
- 4.1、隐函数的导数
- 4.2、由参数方程所确定的函数的导数
- 4.3、相关变化率
- 5、函数的微分
- 5.1、引例
- 5.2、定义
- 5.3、可微与可导
- 5.4、微分的几何意义
- 5.5、微分的运算法则

1、导数的概念
1.1、引例
1.1.1、变速直线运动瞬时速度
这个问题描述的是,假设有一个物品从 a a a时刻一直运动到 b b b时刻,如何刻画它在 ( a , b ) (a,b) (a,b)上的某一点的速度呢?
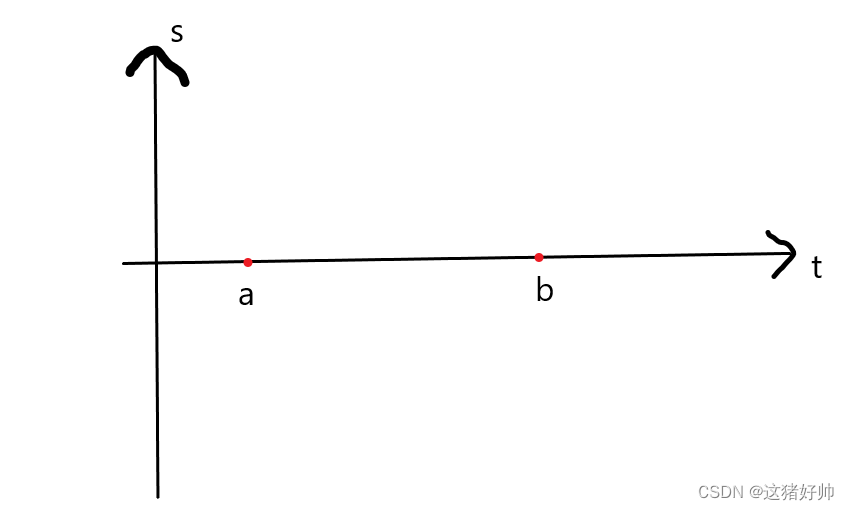
s = f ( t ) s = f(t) s=f(t)
第一种情况:匀速
如果是匀速直线运动的话,即我们算出这一段路程的位移,再算出它的时间,两个相除即为速度
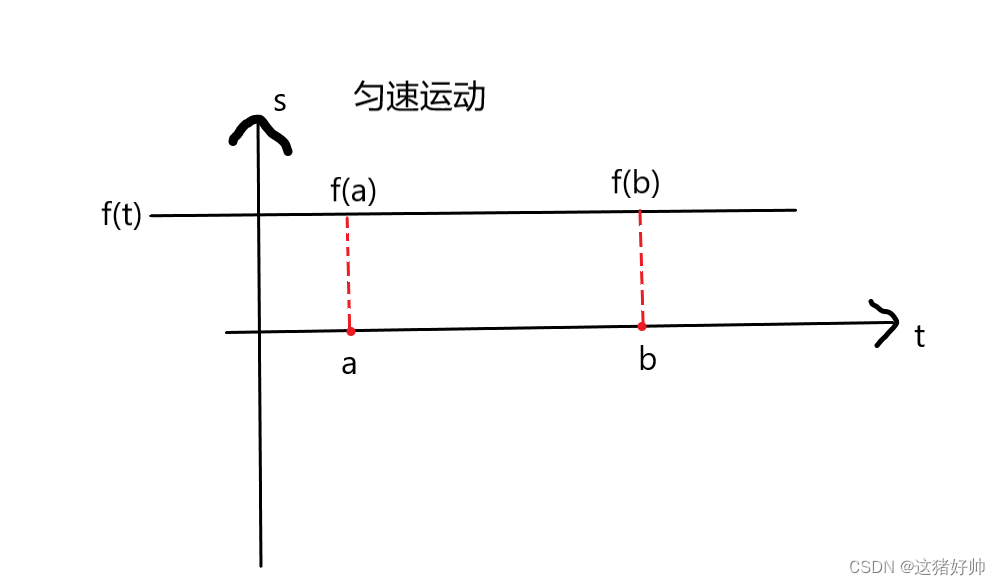
v = f ( b ) − f ( a ) b − a v=\frac{f(b)-f(a)}{b-a} v=b−af(b)−f(a)
第二种情况:变速
变速运动我们想要看某一点上的瞬时速度,尝试能不能转化为第一种匀速的情况呢?
如果我们想看一点 t 0 t_0 t0的瞬时速度,那么我们就想到取一个 Δ t \Delta t Δt,如果这个 Δ t \Delta t Δt足够小, t 0 + Δ t t_0+\Delta t t0+Δt的变化肯定小,那么它的速度变化也肯定是比较小的,也就近似可以看成是一段匀速运动
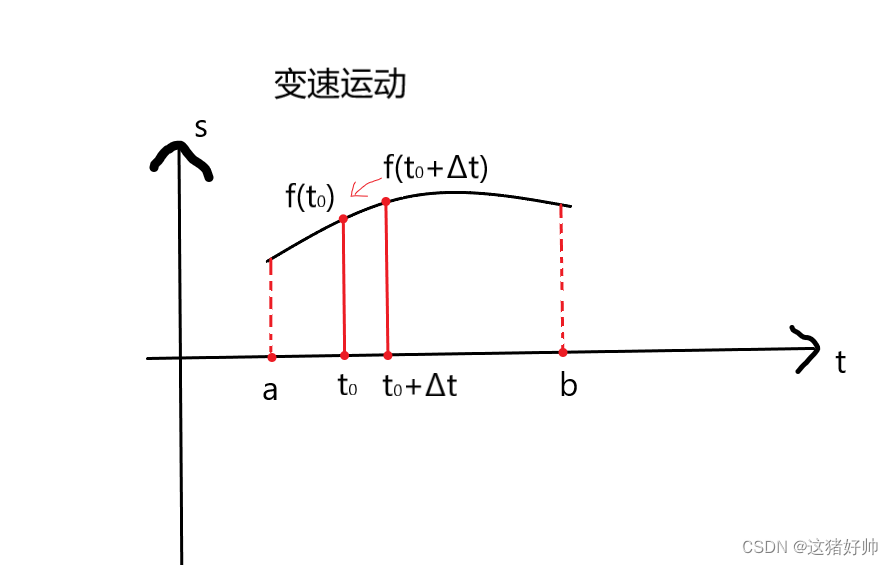
当 t 0 t_0 t0与 t 0 + Δ t t_0+\Delta t t0+Δt非常接近时,近似一个匀速运动,匀速运动的平均速度即为:
f ( t 0 + Δ x ) − f ( t 0 ) Δ x = 平均速度 ≈ 瞬时速度 \frac{f(t_0+\Delta x)-f(t_0)}{\Delta x}=平均速度\approx 瞬时速度 Δxf(t0+Δx)−f(t0)=平均速度≈瞬时速度
而上面的接近过程就可以用极限来表示:
lim Δ t → 0 f ( t 0 + Δ t ) − f ( t 0 ) Δ t \lim_{\Delta t \to 0}\frac{f(t_0+\Delta t)-f(t_0)}{\Delta t} Δt→0limΔtf(t0+Δt)−f(t0)
此时平均速度就转化为了 t 0 t_0 t0这一点的瞬时速度
1.1.2、曲线的切线
f ( x ) f(x) f(x)上有两点 ( x 0 , f ( x 0 ) ) , ( x 0 + Δ x , f ( x 0 + Δ x ) ) , (x_0,f(x_0)),(x_0+\Delta x,f(x_0+\Delta x)), (x0,f(x0)),(x0+Δx,f(x0+Δx)),过这两点做一条直线,记为割线
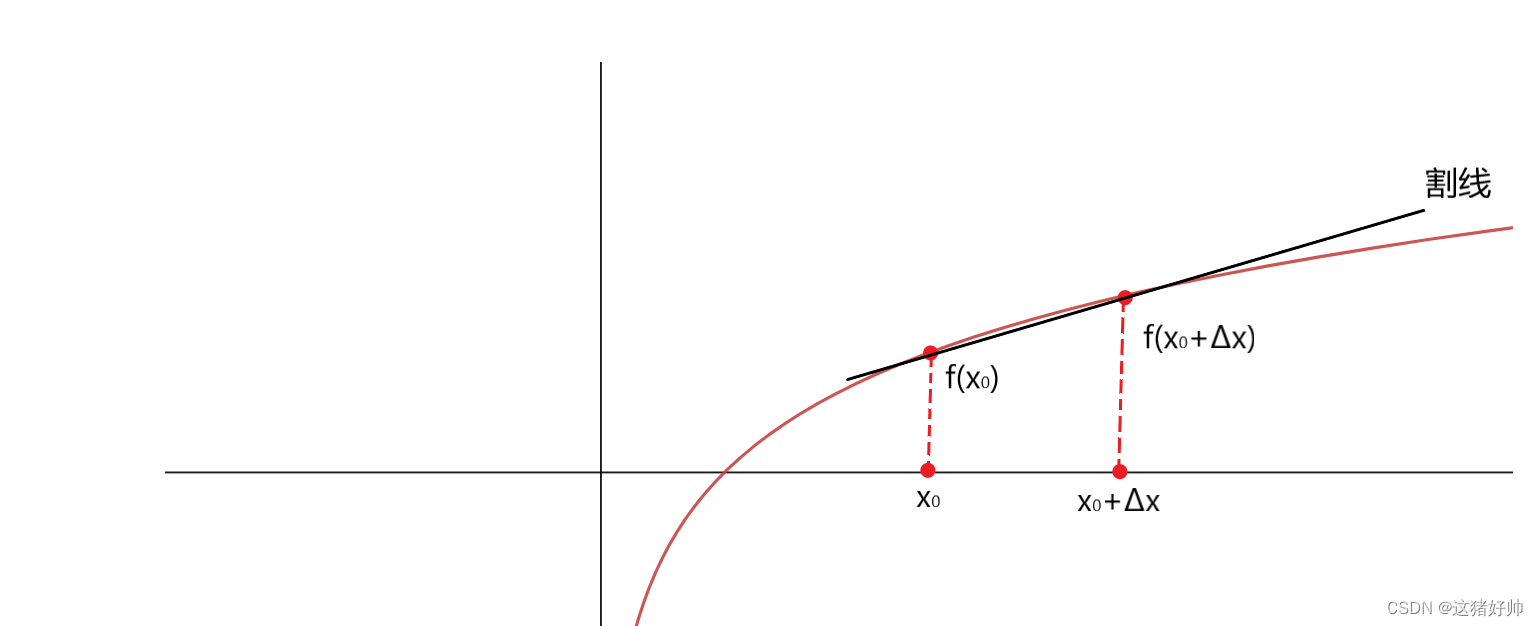
割线的斜率 k 割 = f ( x 0 + Δ x ) − f ( x 0 ) Δ x k_割=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} k割=Δxf(x0+Δx)−f(x0)
而当 x 0 + Δ x 与 x 0 x_0+\Delta x与x_0 x0+Δx与x0无限接近时按照做割线的方法再做一条线,即割线的极限,记为切线
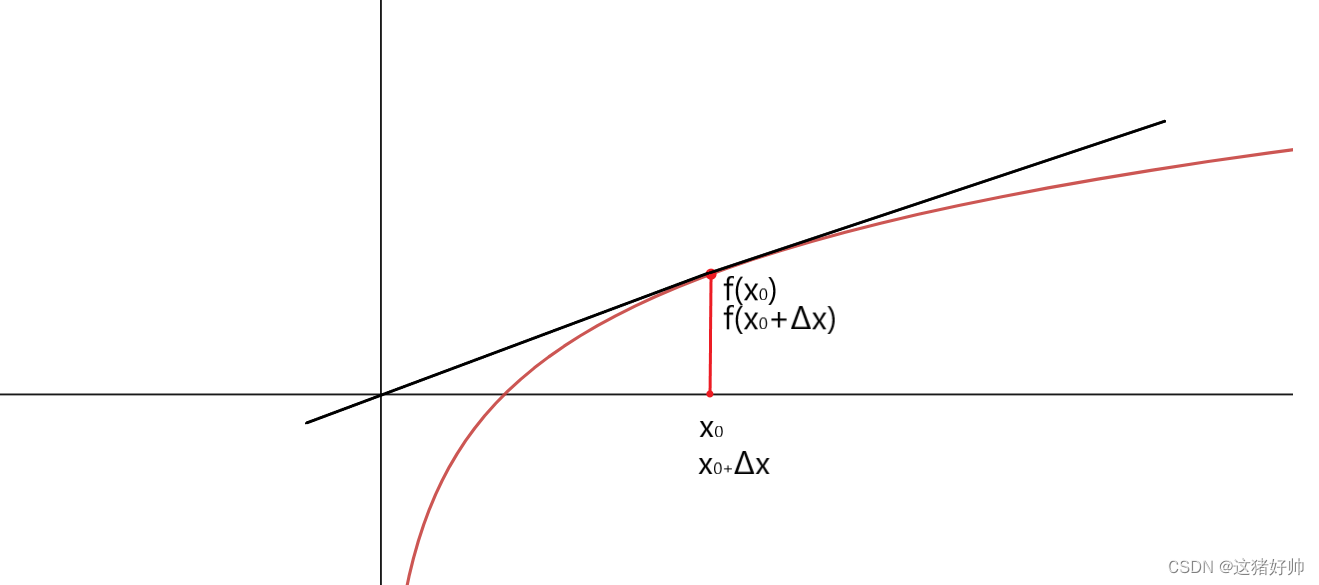
而既然割线的斜率我们知道怎么求,那自然切线的斜率也就出来了,只要取一个极限即可
k 切 = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x k_切=\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} k切=limΔx→0Δxf(x0+Δx)−f(x0)
1.2、导数的定义
定义:若 lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x \lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} limΔx→0Δxf(x0+Δx)−f(x0)存在
则称 f ( x ) f(x) f(x)在 x 0 x_0 x0点可导,记作: f ′ ( x ) = y ′ ∣ x = x 0 = d y d x ∣ x = x 0 f^\prime(x)=y\prime|_{x = x_0}=\frac{dy}{dx}|_{x = x_0} f′(x)=y′∣x=x0=dxdy∣x=x0
f ′ ( x 0 ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 = lim Δ x → 0 Δ y Δ x f^\prime(x_0)=\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\lim_{x \to x_0}\frac{f(x)-f(x_0)}{x - x_0}=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x} f′(x0)=Δx→0limΔxf(x0+Δx)−f(x0)=x→x0limx−x0f(x)−f(x0)=Δx→0limΔxΔy
若以上极限不存在,则称 f ( x ) f(x) f(x)在 x 0 x_0 x0处不可导
若极限为无穷大,则称 f ( x ) f(x) f(x)在 x 0 x_0 x0处导数为无穷大
左导数定义: f − ′ ( x 0 ) = lim Δ x → 0 − f ( x 0 + Δ x ) − f ( x 0 ) Δ x = lim x → x 0 − f ( x ) − f ( x 0 ) x − x 0 f^\prime_-(x_0)=\lim_{\Delta x \to 0^-}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\lim_{x \to x_0^-}\frac{f(x)-f(x_0)}{x - x_0} f−′(x0)=Δx→0−limΔxf(x0+Δx)−f(x0)=x→x0−limx−x0f(x)−f(x0)
右导数定义: f + ′ ( x 0 ) = lim Δ x → 0 + f ( x 0 + Δ x ) − f ( x 0 ) Δ x = lim x → x 0 + f ( x ) − f ( x 0 ) x − x 0 f^\prime_+(x_0)=\lim_{\Delta x \to 0^+}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\lim_{x \to x_0^+}\frac{f(x)-f(x_0)}{x - x_0} f+′(x0)=Δx→0+limΔxf(x0+Δx)−f(x0)=x→x0+limx−x0f(x)−f(x0)
左右导数与导数的关系:可导 ⇚ ⇛ \Lleftarrow\Rrightarrow ⇚⇛左右导数存在且相等
区间上可导:
1、若 f ( x ) f(x) f(x)开区间 ( a , b ) (a,b) (a,b)上每一点都可导,而每一点的函数值形成的新函数我们称为导函数,记为 f ′ ( x ) , x ∈ ( a , b ) f^\prime(x),x\in(a,b) f′(x),x∈(a,b)
2、若上述区间为闭区间 [ a , b ] [a,b] [a,b],那么不仅要求区间内每点可导,而且还要求端点 a a a右可导,端点 b b b左可导
1.3、证明常用导数
(1)、 ( x α ) ′ = a x α − 1 ( x > 0 ) (x^\alpha)^\prime = ax^{\alpha-1}(x >0) (xα)′=axα−1(x>0)
【证明】
lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = ( x + Δ x ) α − x α Δ x \lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{(x+\Delta x)^\alpha-x^\alpha}{\Delta x} limΔx→0Δxf(x+Δx)−f(x)=Δx(x+Δx)α−xα
= x α [ ( 1 + Δ x x ) α − 1 ] Δ x = x α α Δ x x Δ x = α x α − 1 =\frac{x^\alpha[(1+\frac{\Delta x}{x})^\alpha-1]}{\Delta x}=\frac{x^\alpha\alpha\frac{\Delta x}{x}}{\Delta x}=\alpha x^{\alpha -1} =Δxxα[(1+xΔx)α−1]=ΔxxααxΔx=αxα−1
(2)、 ( a x ) ′ = a x ln a ( a > 0 , a ≠ 1 ) (a^x)^\prime=a^x\ln a (a>0,a≠1) (ax)′=axlna(a>0,a=1)
【证明】
由 lim x → 0 a x − 1 ∼ x ln a \lim_{x \to 0}a^x-1\sim x\ln a limx→0ax−1∼xlna
lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = lim Δ x → 0 a x + Δ x − a x Δ x = lim Δ x → 0 a x [ a Δ x − 1 ] Δ x = lim Δ x → 0 a x Δ x ln a Δ x = a x ln a \lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\lim_{\Delta x \to 0}\frac{a^{x+\Delta x}-a^x}{\Delta x}=\lim_{\Delta x \to 0}\frac{a^x[a^{\Delta x}-1]}{\Delta x}=\lim_{\Delta x \to 0}\frac{a^x\Delta x\ln a}{\Delta x}=a^x\ln a limΔx→0Δxf(x+Δx)−f(x)=limΔx→0Δxax+Δx−ax=limΔx→0Δxax[aΔx−1]=limΔx→0ΔxaxΔxlna=axlna
(3)、 ( log a x ) ′ = 1 x ln a ( a > 0 , a ≠ 1 ) (\log_ax)^\prime=\frac{1}{x\ln a}(a>0,a≠1) (logax)′=xlna1(a>0,a=1)
【证明】
由 lim x → 0 log a ( 1 + x ) ∼ x ln a \lim_{x \to 0}\log_a(1+x)\sim x\ln a limx→0loga(1+x)∼xlna
lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = lim Δ x → 0 log a ( x + Δ x ) − log a x Δ x = lim Δ x → 0 log a ( 1 + Δ x x ) Δ x = lim Δ x → 0 Δ x x ln x Δ x = 1 x ln x \lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\lim_{\Delta x \to 0}\frac{\log_a(x+\Delta x)-\log_a{x}}{\Delta x}=\lim_{\Delta x \to 0}\frac{\log_a(1+\frac{\Delta x}{x})}{\Delta x}=\lim_{\Delta x \to 0}\frac{\frac{\Delta x}{x\ln x}}{\Delta x}=\frac{1}{x\ln x} limΔx→0Δxf(x+Δx)−f(x)=limΔx→0Δxloga(x+Δx)−logax=limΔx→0Δxloga(1+xΔx)=limΔx→0ΔxxlnxΔx=xlnx1
(4)、 ( sin x ) ′ = cos x (\sin x)^\prime=\cos x (sinx)′=cosx
【证明】
lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = sin ( x + Δ x ) − sin x Δ x = 2 sin ( Δ x 2 ) × cos ( 2 x + Δ x 2 ) Δ x = 2 Δ x 2 cos ( 2 x + Δ x 2 ) Δ x = cos x \lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{\sin(x+\Delta x)-\sin x}{\Delta x}=\frac{2\sin(\frac{\Delta x}{2})\times \cos(\frac{2x+\Delta x}{2})}{\Delta x}=\frac{2\frac{\Delta x}{2}\cos(\frac{2x+\Delta x}{2})}{\Delta x}=\cos x limΔx→0Δxf(x+Δx)−f(x)=Δxsin(x+Δx)−sinx=Δx2sin(2Δx)×cos(22x+Δx)=Δx22Δxcos(22x+Δx)=cosx
(5)、 ( cos x ) ′ = − sin x (\cos x)^\prime=-\sin x (cosx)′=−sinx
【证明】
lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = cos ( x + Δ x ) − cos x Δ x = − 2 sin ( 2 x + Δ x 2 ) sin ( Δ x 2 ) Δ x = − 2 Δ x 2 sin ( 2 x + Δ x 2 ) Δ x = − sin x \lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{\cos(x+\Delta x)-\cos x}{\Delta x}=\frac{-2\sin(\frac{2x+\Delta x}{2})\sin(\frac{\Delta x}{2})}{\Delta x}=\frac{-2\frac{\Delta x}{2}\sin(\frac{2x+\Delta x}{2})}{\Delta x}=-\sin x limΔx→0Δxf(x+Δx)−f(x)=Δxcos(x+Δx)−cosx=Δx−2sin(22x+Δx)sin(2Δx)=Δx−22Δxsin(22x+Δx)=−sinx
1.4、导数的几何意义
在引例中,我们详细说过导数的几何意义
导数 f ′ ( x 0 ) f^\prime(x_0) f′(x0)在几何上表示曲线 y = f ( x ) y=f(x) y=f(x)在点 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0))处切线的斜率
切线方程: y − y 0 = f ′ ( x 0 ) ( x − x 0 ) y-y_0=f^\prime(x_0)(x-x_0) y−y0=f′(x0)(x−x0)
法线方程: y − y 0 = − 1 f ′ ( x 0 ) ( x − x 0 ) y-y_0 = -\frac{1}{f^\prime(x_0)}(x-x_0) y−y0=−f′(x0)1(x−x0)
1.5、可导与连续的关系
可导 ⇛ ⇛ ⇛ 连续
【证明】
即证: lim Δ x → 0 Δ y = 0 \lim_{Δ x → 0}Δ y=0 limΔx→0Δy=0
∵ Δ y = Δ y Δ x Δ x ∵Δ y=\frac{Δ y}{Δ x}Δ x ∵Δy=ΔxΔyΔx
∵ Δ y Δ x → 0 , Δ x → 0 ∵\frac{Δ y}{Δ x}\to 0,Δ x→0 ∵ΔxΔy→0,Δx→0
∴ lim Δ x → 0 Δ y = 0 ∴\lim_{Δ x\to0}Δ y=0 ∴limΔx→0Δy=0
证毕
注意:连续无法推出可导
例如:
1、 y = ∣ x ∣ y=|x| y=∣x∣在 x = 0 x=0 x=0处虽然连续,并且左右导数都存在,但它的左右导数并不相等,故不可导
2、 y = x 1 3 y=x^\frac{1}{3} y=x31在 x = 0 x=0 x=0处虽然连续,并且也有一条切线y轴,但它的导数是无穷大,故也不可导
3、 y = { x sin 1 x x ≠ 0 0 , x = 0 y=\begin{cases} x\sin\frac{1}{x} & x≠0 \\ 0, & x=0 \\ \end{cases} y={xsinx10,x=0x=0,虽然这个函数连续,但左右导数都不存在,故不可导
2、函数的求导法则
2.1、函数的和、差、积、商的求导法则
定理1、设 u ( x ) , v ( x ) u(x),v(x) u(x),v(x)都可导,则
1、 ( u ± v ) ′ = u ′ ± v ′ (u ± v)^′=u^′±v^′ (u±v)′=u′±v′
2、 ( u v ) ′ = u ′ v + u v ′ (uv)^′=u^′v+uv^′ (uv)′=u′v+uv′
3、 ( u v ) ′ = u ′ v − v ′ u v 2 ( v ≠ 0 ) (\frac{u}{v})^′=\frac{u^′v-v^′u}{v^2}(v≠0) (vu)′=v2u′v−v′u(v=0)
【证明: ( u + v ) ′ = u ′ + v ′ (u+v)^′=u^′+v^′ (u+v)′=u′+v′】
f ( x + Δ x ) − f ( x ) Δ x = u ( x + Δ x ) + v ( x + Δ x ) − u ( x ) − v ( x ) Δ x \frac{f(x+Δx)-f(x)}{Δx}=\frac{u(x+Δx)+v(x+Δx)-u(x)-v(x)}{Δx} Δxf(x+Δx)−f(x)=Δxu(x+Δx)+v(x+Δx)−u(x)−v(x)
故: lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = lim Δ x → 0 u ( x + Δ x ) − u ( x ) Δ x + lim Δ x → 0 v ( x + Δ x ) − v ( x ) Δ x = u ′ + v ′ \lim_{Δx→0}\frac{f(x+Δx)−f(x)}{Δx}=\lim_{Δx→0}\frac{u(x+Δx)-u(x)}{Δx}+\lim_{Δx→0}\frac{v(x+Δx)-v(x)}{Δx}=u^′+v^′ limΔx→0Δxf(x+Δx)−f(x)=limΔx→0Δxu(x+Δx)−u(x)+limΔx→0Δxv(x+Δx)−v(x)=u′+v′
证毕
【证明: ( u v ) ′ = u ′ v + u v ′ (uv)^′=u^′v+uv^′ (uv)′=u′v+uv′】
f ( x + Δ x ) − f ( x ) Δ x = u ( x + Δ x ) v ( x + Δ x ) − u ( x ) v ( x ) Δ x \frac{f(x+Δx)-f(x)}{Δx}=\frac{u(x+Δx)v(x+Δx)-u(x)v(x)}{Δx} Δxf(x+Δx)−f(x)=Δxu(x+Δx)v(x+Δx)−u(x)v(x)
= u ( x + Δ x ) v ( x + Δ x ) − u ( x ) v ( x + Δ x ) + u ( x ) v ( x + Δ x ) − u ( x ) v ( x ) Δ x =\frac{u(x+Δx)v(x+Δx)-u(x)v(x+Δx)+u(x)v(x+Δx)-u(x)v(x)}{Δx} =Δxu(x+Δx)v(x+Δx)−u(x)v(x+Δx)+u(x)v(x+Δx)−u(x)v(x)
故: lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = lim Δ x → 0 u ( x + Δ x ) v ( x + Δ x ) − u ( x ) v ( x + Δ x ) Δ x + lim Δ x → 0 u ( x ) v ( x + Δ x ) − u ( x ) v ( x ) Δ x \lim_{Δx→0}\frac{ f(x+Δx)−f(x) }{Δx}=\lim_{Δx→0}\frac{u(x+Δx)v(x+Δx)−u(x)v(x+Δx)}{Δx}+\lim_{Δx→0}\frac{u(x)v(x+Δx)−u(x)v(x)}{Δx} limΔx→0Δxf(x+Δx)−f(x)=limΔx→0Δxu(x+Δx)v(x+Δx)−u(x)v(x+Δx)+limΔx→0Δxu(x)v(x+Δx)−u(x)v(x)
= u ′ v + u v ′ =u^′v+uv^′ =u′v+uv′
证毕
【证明: ( u v ) ′ = u ′ v − v ′ u v 2 ( v ≠ 0 ) (\frac{u}{v})^′=\frac{u^′v-v^′u}{v^2}(v≠0) (vu)′=v2u′v−v′u(v=0)】
f ( x + Δ x ) − f ( x ) Δ x = u ( x + Δ x ) v ( x + Δ x ) − u ( x ) v ( x ) Δ x = u ( x + Δ x ) v ( x ) − u ( x ) v ( x + Δ x ) v ( x + Δ x ) v ( x ) Δ x \frac{f(x+Δx)-f(x)}{Δx}=\frac{\frac{u(x+Δx)}{v(x+Δx)}-\frac{u(x)}{v(x)}}{Δx}=\frac{u(x+Δx)v(x)-u(x)v(x+Δx)}{v(x+Δx)v(x)Δx} Δxf(x+Δx)−f(x)=Δxv(x+Δx)u(x+Δx)−v(x)u(x)=v(x+Δx)v(x)Δxu(x+Δx)v(x)−u(x)v(x+Δx)
= u ( x + Δ x ) v ( x ) − u ( x ) v ( x ) + u ( x ) v ( x ) − u ( x ) v ( x + Δ x ) v ( x + Δ x ) v ( x ) Δ x =\frac{u(x+Δx)v(x)-u(x)v(x)+u(x)v(x)-u(x)v(x+Δx)}{v(x+Δx)v(x)Δx} =v(x+Δx)v(x)Δxu(x+Δx)v(x)−u(x)v(x)+u(x)v(x)−u(x)v(x+Δx)
即: lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = lim Δ x → 0 u ( x + Δ x ) v ( x ) − u ( x ) v ( x ) + u ( x ) v ( x ) − u ( x ) v ( x + Δ x ) v ( x + Δ x ) v ( x ) Δ x = u ′ v − u v ′ v 2 \lim_{Δx →0}\frac{f(x+Δx)-f(x)}{Δx}=\lim_{Δx \to 0}\frac{u(x+Δx)v(x)-u(x)v(x)+u(x)v(x)-u(x)v(x+Δx)}{v(x+Δx)v(x)Δx}=\frac{u^′v-uv^′}{v^2} limΔx→0Δxf(x+Δx)−f(x)=limΔx→0v(x+Δx)v(x)Δxu(x+Δx)v(x)−u(x)v(x)+u(x)v(x)−u(x)v(x+Δx)=v2u′v−uv′
证毕
2.2、反函数的求导法则
定理:设区间 I I I上严格单调且连续的函数 x = f ( y ) x=f(y) x=f(y)在 y y y处可导,且 f ′ ( y ) ≠ 0 , f^′(y)≠0, f′(y)=0,则它的反函数 y = f − 1 ( x ) y=f^{-1}(x) y=f−1(x)在对应点可导,且 ( f − 1 ) ′ ( x ) = 1 f ′ ( y ) , d y d x = 1 d x d y (f^{-1})^′(x)=\frac{1}{f^′(y)},\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}} (f−1)′(x)=f′(y)1,dxdy=dydx1
注意:严格单调且连续是为了保证一定有反函数
1 、 ( arcsin x ) ′ = 1 1 − x 2 1、(\arcsin x)^′ = \frac{1}{\sqrt{1-x^2}} 1、(arcsinx)′=1−x21
2 、 ( arccos x ) ′ = − 1 1 − x 2 2、(\arccos x)^′=-\frac{1}{\sqrt{1-x^2}} 2、(arccosx)′=−1−x21
3 、 ( arctan x ) ′ = 1 1 + x 2 3、(\arctan x)^′=\frac{1}{1+x^2} 3、(arctanx)′=1+x21
4 、 ( a r c c o t x ) ′ = − 1 1 + x 2 4、(arccot\ x)^′=-\frac{1}{1+x^2} 4、(arccot x)′=−1+x21
【证明 ( arcsin x ) ′ = 1 1 − x 2 (\arcsin x)^′ = \frac{1}{\sqrt{1-x^2}} (arcsinx)′=1−x21】
y = arcsin x y = \arcsin x y=arcsinx 的反函数为 x = sin y x=\sin y x=siny
根据反函数的求导反则: ( arcsin x ) ′ = 1 ( sin y ) ′ = 1 cos y = 1 1 − sin 2 y = 1 1 − x 2 (\arcsin x)^′=\frac{1}{(\sin y)^′}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-\sin^2y}}=\frac{1}{\sqrt{1-x^2}} (arcsinx)′=(siny)′1=cosy1=1−sin2y1=1−x21
另外三个同理
2.3、复合函数的求导法则
定理(链式法则):设 u = g ( x ) u=g(x) u=g(x)在 x x x可导, y = f ( u ) y=f(u) y=f(u)在对应 u u u处可导,则 y = f [ g ( x ) ] y=f[g(x)] y=f[g(x)]在 x x x处可导,且 d y d x = d y d u d u d x = f ′ ( u ) g ′ ( x ) \frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}=f^′(u)g^′(x) dxdy=dudydxdu=f′(u)g′(x)
2.4、基本初等函数的导数公式
1 、 ( C ) ′ = 0 1、(C)^′=0 1、(C)′=0
2 、 ( x a ) ′ = a x a − 1 2、(x^a)^′=ax^{a-1} 2、(xa)′=axa−1
3 、 ( a x ) ′ = a x ln a 3、(a^x)^′=a^x\ln a 3、(ax)′=axlna
4 、 ( e x ) ′ = e x 4、(e^x)^′=e^x 4、(ex)′=ex
5 、 ( log a x ) ′ = 1 x ln a 5、(\log_ax)^′=\frac{1}{x\ln a} 5、(logax)′=xlna1
6 、 ( ln ∣ x ∣ ) ′ = 1 x 6、(\ln |x|)^′=\frac{1}{x} 6、(ln∣x∣)′=x1
7 、 ( sin x ) ′ = cos x 7、(\sin x)^′=\cos x 7、(sinx)′=cosx
8 、 ( cos x ) ′ = − sin x 8、(\cos x)^′=-\sin x 8、(cosx)′=−sinx
9 、 ( tan x ) ′ = sec 2 x 9、(\tan x)^′=\sec^2x 9、(tanx)′=sec2x
10 、 ( cot x ) ′ = − csc 2 x 10、(\cot x)^′=-\csc^2x 10、(cotx)′=−csc2x
11 、 ( sec x ) ′ = sec x tan x 11、(\sec x)^′=\sec x\tan x 11、(secx)′=secxtanx
12 、 ( csc x ) ′ = − csc x cot x 12、(\csc x)^′=-\csc x\cot x 12、(cscx)′=−cscxcotx
13 、 ( arcsin x ) ′ = 1 1 − x 2 13、(\arcsin x)^′=\frac{1}{\sqrt{1-x^2}} 13、(arcsinx)′=1−x21
14 、 ( arccos x ) ′ = − 1 1 − x 2 14、(\arccos x)^′=-\frac{1}{\sqrt{1-x^2}} 14、(arccosx)′=−1−x21
15 、 ( arctan x ) ′ = 1 1 + x 2 15、(\arctan x)^′=\frac{1}{1+x^2} 15、(arctanx)′=1+x21
16 、 ( a r c c o t x ) ′ = − 1 1 + x 2 16、(arccot\ x)^′=-\frac{1}{1+x^2} 16、(arccot x)′=−1+x21
3、高阶导数
在前面,我们学习了的都是一阶导数,也就是对一个函数求一次导得到的函数就叫做一阶导数
当我们对一个函数求了一次导数后,会得到一个导函数,如果这个导函数是可导的,我们再对他求导,就会得到二阶导数,以此类推
二阶导数: ( y ′ ) ′ = y ′ ′ = d 2 y d x 2 (y')'=y''=\frac{d^2y}{dx^2} (y′)′=y′′=dx2d2y
三阶: y ′ ′ ′ y''' y′′′
四阶: y ( 4 ) y^{(4)} y(4)
. . . ... ...
n阶: y ( n ) = d n y d x n y^{(n)}=\frac{d^ny}{dx^n} y(n)=dxndny
若 f ( n ) ( x ) f^{(n)}(x) f(n)(x)在区间 I I I上连续,称 f ( x ) f(x) f(x)在 I I I上n阶连续可导
3.1、高阶导数的公式
设 u , v u,v u,v都是 n n n阶可导,则:
1 、 ( u ± v ) ( n ) = u ( n ) ± v ( n ) 1、(u±v)^{(n)}=u^{(n)}±v^{(n)} 1、(u±v)(n)=u(n)±v(n)
2 、 L e i b n i z 2、Leibniz 2、Leibniz公式 ( u v ) ( n ) = ∑ k = 0 n C n k u ( n − k ) v k (uv)^{(n)}=\sum_{k=0}^nC^k_nu^{(n-k)}v^k (uv)(n)=∑k=0nCnku(n−k)vk
3 、 ( sin x ) ( n ) = sin ( x + n π 2 ) 3、(\sin x)^{(n)}=\sin(x+n\frac{π}{2}) 3、(sinx)(n)=sin(x+n2π)
4 、 ( cos x ) ( n ) = cos ( x + n π 2 ) 4、(\cos x)^{(n)}=\cos(x+n\frac{π}{2}) 4、(cosx)(n)=cos(x+n2π)
4、隐函数和参数方程确定的函数的导数
4.1、隐函数的导数
显函数:因变量 f ( x ) f(x) f(x)可以通过自变量 x x x表示的函数叫做显函数
例如: y = cos x , y = x 1 + x y = \cos x,y=\frac{x}{1+x} y=cosx,y=1+xx
隐函数: 因变量 f ( x ) f(x) f(x)不能通过自变量 x x x表示出来叫做隐函数
例如: 3 y + x + 1 = 0 3y+x+1=0 3y+x+1=0
上述的隐函数可以显化为显函数 y = − x + 1 3 y=-\frac{x+1}{3} y=−3x+1
但并不是每一个隐函数都可以显化为显函数的
例如: y − x − ϵ sin y = 0 ( 0 < ϵ < 1 ) y-x-ϵ\sin y=0(0<ϵ<1) y−x−ϵsiny=0(0<ϵ<1)
那么,既然有上述这种很难显化的隐函数,那么我们就要确定一种隐函数的通用求导法则,即:
F ( x , y ) = 0 , y = f ( x ) , F ( x , f ( x ) ) = 0 F(x,y)=0,y=f(x),F(x,f(x))=0 F(x,y)=0,y=f(x),F(x,f(x))=0
此时两边同时对x求导,即可
例如:求由方程 y 5 + 2 y − x = 0 y^5+2y-x=0 y5+2y−x=0确定的隐函数 y = f ( x ) y=f(x) y=f(x)的导数
解: ( y 5 + 2 y − x ) ′ = 5 y 4 y ′ + 2 y ′ − 1 (y^5+2y-x)'=5y^4y'+2y'-1 (y5+2y−x)′=5y4y′+2y′−1
y ′ ( 5 y 4 + 2 ) = 1 y'(5y^4+2)=1 y′(5y4+2)=1
y ′ = 1 5 y 4 + 2 y'=\frac{1}{5y^4+2} y′=5y4+21
4.2、由参数方程所确定的函数的导数
定理:设 x = φ ( t ) , y = ψ ( t ) x=φ(t),y=ψ(t) x=φ(t),y=ψ(t)在 ( α , β ) (α,β) (α,β)上可导, φ ′ ( t ) ≠ 0 , φ'(t)≠0, φ′(t)=0,则 d y d x = ψ ′ ( t ) φ ′ ( t ) \frac{dy}{dx}=\frac{ψ'(t)}{φ'(t)} dxdy=φ′(t)ψ′(t)
若 φ ( t ) , ψ ( t ) φ(t),ψ(t) φ(t),ψ(t)二阶可导,则 d 2 y d x 2 = ψ ′ ′ ( t ) φ ′ ( t ) − φ ′ ′ ( t ) ψ ′ ( t ) φ ′ 3 ( t ) \frac{d^2y}{dx^2}=\frac{ψ''(t)φ'(t)-φ''(t)ψ'(t)}{φ'^3(t)} dx2d2y=φ′3(t)ψ′′(t)φ′(t)−φ′′(t)ψ′(t)
首先根据条件: φ ′ ( t ) ≠ 0 φ'(t)≠0 φ′(t)=0我们可以得到 φ ( t ) φ(t) φ(t)在 ( α , β ) (α,β) (α,β)上是单调的,那么 x = φ ( t ) x=φ(t) x=φ(t)就有反函数 t = φ − 1 ( x ) t=φ^{-1}(x) t=φ−1(x)
① y = ψ ( t ) , ② t = φ − 1 ( x ) ①y=ψ(t),②t=φ^{-1}(x) ①y=ψ(t),②t=φ−1(x)
由①②得它的导数为 d y d x = d y d t d t d x = ψ ′ ( t ) φ ′ ( t ) \frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}=\frac{ψ'(t)}{φ'(t)} dxdy=dtdydxdt=φ′(t)ψ′(t)
而若 ψ ( t ) , φ ( t ) ψ(t),φ(t) ψ(t),φ(t)二阶可导,则两边再同时对x求一次导得:
d 2 y d x 2 = d d t ( ψ ′ ( t ) φ ′ ( t ) ) × d t d x \frac{d^2y}{dx^2}=\frac{d}{dt} (\frac{ψ'(t)}{φ'(t)})×\frac{dt}{dx} dx2d2y=dtd(φ′(t)ψ′(t))×dxdt
= ψ ′ ′ ( t ) φ ′ ( t ) − φ ′ ′ ( t ) ψ ′ ( t ) φ ′ 2 ( t ) × 1 φ ′ ( t ) =\frac{ψ''(t)φ'(t)-φ''(t)ψ'(t)}{φ'^2(t)}×\frac{1}{φ'(t)} =φ′2(t)ψ′′(t)φ′(t)−φ′′(t)ψ′(t)×φ′(t)1
4.3、相关变化率
相变变化率:即 x = x ( t ) , y = y ( t ) x=x(t),y=y(t) x=x(t),y=y(t),并且 x x x和 y y y之间又满足某种关系 F ( x , y ) = 0 F(x,y)=0 F(x,y)=0,那么我们如果知道了 x / y x/y x/y中任意一个变量对t的变化率就可以求出另一个变量与t之间的变化率
例:设有一个倒置的圆锥形容器,其底面圆直径为10cm,高为5cm,现以每秒3cm 3 ^3 3给容器中加水,试求t = 1秒时水面上升的速率
【解】
设水的高度为 h ( t ) h(t) h(t),则水的体积 V ( t ) = π 3 h 2 ( t ) × h ( t ) V(t)=\frac{π}{3}h^2(t)×h(t) V(t)=3πh2(t)×h(t)
V ′ ( t ) = π h 2 ( t ) d h d t = 3 V'(t)=πh^2(t)\frac{dh}{dt}=3 V′(t)=πh2(t)dtdh=3
由题得: V ( 1 ) = 3 = π 3 h 3 ( 1 ) , h ( 1 ) = 3 9 π V(1)=3=\frac{π}{3}h^3(1),h(1)=^3\sqrt{\frac{9}{π}} V(1)=3=3πh3(1),h(1)=3π9
那么 V ′ ( 1 ) = 3 = π ( 9 π ) 2 3 d h d t V'(1)=3=π(\frac{9}{π})^\frac{2}{3}\frac{dh}{dt} V′(1)=3=π(π9)32dtdh
d h d t = 3 π ( 9 π ) − 2 3 \frac{dh}{dt}=\frac{3}{π}(\frac{9}{π})^{-\frac{2}{3}} dtdh=π3(π9)−32
相关变化率解题方法:
1.先建立两个相关变化率的关系式 F ( x , y ) F(x,y) F(x,y)如例题中的体积变化率与高度变化率的关系
2.两边同时对t求导,得到未知相关变化率
5、函数的微分
5.1、引例
当我们得到一个函数时,我们需要计算它从某点 x 0 x_0 x0经过一个变化到达 x 0 + Δ x x_0+Δx x0+Δx时的函数值的改变量
例如: f ( x ) = x 2 f(x)=x^2 f(x)=x2
函数改变量: Δ y = f ( x 0 + Δ x ) − f ( x 0 ) Δy=f(x_0+Δx)-f(x_0) Δy=f(x0+Δx)−f(x0)
其中 x 0 x_0 x0是定点, Δ x Δx Δx是动点
Δ y = ( x 0 + Δ x ) 2 − ( x 0 ) 2 = 2 x 0 Δ x + ( Δ x ) 2 Δy=(x_0+Δx)^2-(x_0)^2=2x_0Δx+(Δx)^2 Δy=(x0+Δx)2−(x0)2=2x0Δx+(Δx)2
我们观察上述式子, ( Δ x ) 2 (Δx)^2 (Δx)2其实是 Δ x Δx Δx的高阶无穷小, 2 x 0 Δ x 2x_0Δx 2x0Δx其实才是 Δ x Δx Δx的同阶无穷小
那么 Δ y ≈ 2 x 0 Δ x Δy\approx 2x_0Δx Δy≈2x0Δx
5.2、定义
微分的定义:若 f ( x 0 + Δ x ) − f ( x 0 ) = A Δ x + o ( Δ x ) f(x_0+Δx)-f(x_0)=AΔx+o(Δx) f(x0+Δx)−f(x0)=AΔx+o(Δx)则称 f ( x ) f(x) f(x)在 x 0 x_0 x0点可微, A Δ x AΔx AΔx称为 f ( x ) f(x) f(x)在 x 0 x_0 x0点的微分,记为: d y = A Δ x dy=AΔx dy=AΔx
1. A Δ x AΔx AΔx是 Δ x Δx Δx的线性函数
2. A Δ x AΔx AΔx是 Δ x Δx Δx的同阶无穷小(主要部分), o ( Δ x ) o(Δx) o(Δx)是 Δ x Δx Δx的高阶无穷小
3. d y dy dy是 Δ y Δy Δy的线性主部
5.3、可微与可导
定理:函数 y = f ( x ) y=f(x) y=f(x)在点 x 0 x_0 x0处可微的充分必要条件是 f ( x ) f(x) f(x)在点 x 0 x_0 x0处可导,且有 d y = f ′ ( x 0 ) Δ x = f ′ ( x ) d x dy=f'(x_0)Δx=f'(x)dx dy=f′(x0)Δx=f′(x)dx
证明:可导 ⇛ \Rrightarrow ⇛可微
f ( x 0 ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x ) Δ x = f ′ ( x 0 ) + α ( x ) f(x_0)=\lim_{Δx \to 0}\frac{f(x_0+Δx)-f(x)}{Δx}=f'(x_0)+α(x) f(x0)=limΔx→0Δxf(x0+Δx)−f(x)=f′(x0)+α(x)
lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) = f ′ ( x 0 ) Δ x + α ( x ) Δ x = f ′ ( x 0 ) Δ x + o ( Δ x ) \lim_{Δx \to 0}f(x_0+Δx)-f(x_0)=f'(x_0)Δx+α(x)Δx=f'(x_0)Δx+o(Δx) limΔx→0f(x0+Δx)−f(x0)=f′(x0)Δx+α(x)Δx=f′(x0)Δx+o(Δx)
证明:可导 ⇚ \Lleftarrow ⇚可微
f ( x 0 + Δ x ) − f ( x 0 ) = A Δ x + o ( Δ x ) f(x_0+Δx)-f(x_0)=AΔx+o(Δx) f(x0+Δx)−f(x0)=AΔx+o(Δx)
f ( x 0 + Δ x ) − f ( x 0 ) Δ x = A + o ( Δ x ) Δ x \frac{f(x_0+Δx)-f(x_0)}{Δx}=A+\frac{o(Δx)}{Δx} Δxf(x0+Δx)−f(x0)=A+Δxo(Δx)
5.4、微分的几何意义
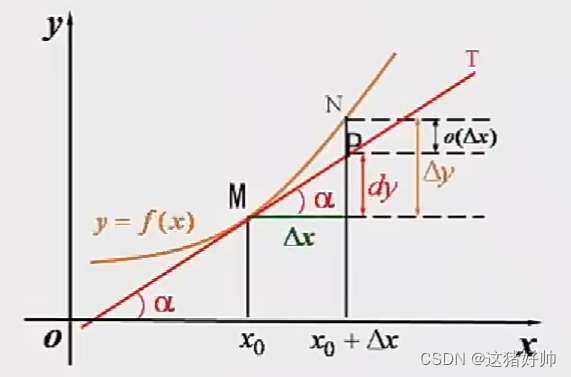
导数的几何意义在一点处的导数就是这一点切线的斜率,就是图中的 tan α \tan α tanα
tan α = d y Δ x , d y = t a n α Δ x = f ′ ( x ) Δ x \tan α=\frac{dy}{Δx},dy=tanαΔx=f'(x)Δx tanα=Δxdy,dy=tanαΔx=f′(x)Δx
微分 d y = f ′ ( x ) d x dy=f'(x)dx dy=f′(x)dx在几何上表示曲线 y = f ( x ) y=f(x) y=f(x)的切线上的增量
用通俗的语言来说,函数在这一点处的微分 d y dy dy表示的是在这一点的切线上两个函数值之间的差,而 Δ y Δy Δy表示的是在这一曲线上两个函数值之间的差, Δ y Δy Δy是精确值,而 d y dy dy是近似值,微分的思想就是把曲线用值线表示,把非均匀变化用均匀变化表示
5.5、微分的运算法则
设 u u u和 v v v都可微,则:
1、 d ( u ± v ) = d u ± d v d(u \pm v)=du\pm dv d(u±v)=du±dv
2、 d ( u v ) = v d u + u d v d(uv)=vdu+udv d(uv)=vdu+udv
3、 d ( u v ) = v d u − u d v v 2 ( v ≠ 0 ) d(\frac{u}{v})=\frac{vdu-udv}{v^2}(v ≠0) d(vu)=v2vdu−udv(v=0)
复合函数微分法则
设 y = f ( u ) y=f(u) y=f(u)可微, u = g ( x ) u=g(x) u=g(x)可微,则 y = f ( g ( x ) ) y=f(g(x)) y=f(g(x))可微,且 d y = y x ′ d x = y u ′ u x ′ d x = y u ′ d u dy=y'_xdx=y'_uu'_xdx=y'_udu dy=yx′dx=yu′ux′dx=yu′du
d y = dy= dy=中间变量导数✖中间变量微分=自变量导数✖自变量微分
我们把这个性质就叫做微分形式不变性





)

主机,vmware,virtualbox安装linux/ubuntu/kali/centos stream9/arch)

是什么和重要知识点?)
附源码)




)



