文章目录
- 混淆矩阵
- F-score
- AUC-ROC

更多内容: 茶桁的AI秘籍
Hi, 你好。我是茶桁。
上一节课,咱们讲到了评测指标,并且在文章的最后提到了一个矩阵,我们就从这里开始。
混淆矩阵
在我们实际的工作中,会有一个矩阵,这个矩阵是分析结果常用的。
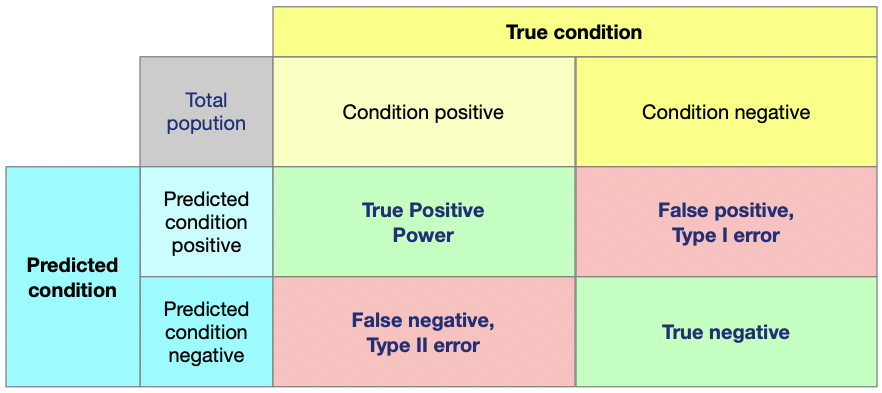
我们来看看具体是什么意思。
所谓的True condition, 指的是真实值, Predicted condition,指的是预测值。
其中行表示,Predicted condition positive表示预测值是1,Predicted condition negative表示预测值是0。
列表示则为:Condition positive表示真实值是1, Condition negative表示真实值是0。
这样行列交叉就组成了这样一个矩阵。这个矩阵叫做混淆矩阵, 英文名字叫做Confusion Matrix.
这个混淆矩阵是什么意思呢?
True Positive 意思就是预测值是1, 预测对了,True negative意思是预测值是0, 预测对了。那相对的, False positive意思就是预测值是1, 预测错了, False negative意思就是预测值是0, 预测错了。
混淆矩阵在常见的机器学习里边是一个很重要的分析工具:
from sklearn.metrics import confusion_matrix
confusion_matrix(true_labels, predicated_labels)—
array([[59, 6],[ 6, 29]])
我们可以直接看看这个方法的源码里有相关说明:
??confusion_matrix---
def confusion_matrix(...the count of true negatives is :math:`C_{0,0}`, false negatives is :math:`C_{1,0}`, true positives is :math:`C_{1,1}` false positives is :math:`C_{0,1}`....
tp实际上是1预测值是1,tn实际是0预测是0, fp实际是0预测是1 fn实际是1预测是0。
這個時候我們再回頭來看上节课结尾处的那个公式:
P r e c i s i o n = t p t p + f p R e c a l l = t p t p + f n \begin{align*} Precision & = \frac{tp}{ tp + fp} \\ Recall & = \frac{tp}{tp + fn} \end{align*} PrecisionRecall=tp+fptp=tp+fntp
很多人看到这个就有点晕, 其实很简单. 切换成我们刚才查看源码时查询到的就就成了这样:
P r e c i s i o n = C ( 0 , 0 ) C ( 0 , 0 ) + C ( 1 , 0 ) R e c a l l = C ( 0 , 0 ) C ( 0 , 0 ) + C ( 0 , 1 ) \begin{align*} Precision & = \frac{C(0, 0)}{ C(0, 0) + C(1, 0)} \\ Recall & = \frac{C(0, 0)}{C(0, 0)+ C(0, 1)} \end{align*} PrecisionRecall=C(0,0)+C(1,0)C(0,0)=C(0,0)+C(0,1)C(0,0)
tp是实际上是positive, 预测也是positive. fp就是实际上并不是positive,但是预测的值是positive. 那么tp+fp就是所有预测为positive的值. 所以precision就是预测对的positive比上所有预测的positive.
fn指的是实际上是positive, 但是预测值并不是positive的值. 所以tp+fn就是所有实际的positive值, recall就是预测对的positive比上所有实际的positive值.
我们这样对比着矩阵和公式来理解Precision和Recall是不是就清晰了很多? 这就是position和recall根据混淆矩阵的一种定义方式.
刚刚讲了baseline, baseline是在做评估的时候要知道结果一定要比什么好才行.如果是个二分类问题, 基本上是一半一半, 准确度是50%, 那基本上就没用.
Precision和recall这两个是针对于分类问题进行评价, 那我们怎么解决回归问题的评价呢?
回归问题,它也有一个accuracy如下:
a c c ( y , y ^ ) = ∑ i ∈ N ∣ y i − y ^ i ∣ a c c ( y , y ^ ) = ∑ i ∈ N ∣ y i − y ^ i ∣ 2 a c c ( y , y ^ ) = ∑ i ∈ N ∣ y i − y i ^ ∣ ∣ y i ∣ acc(y, \hat y) = \sum_{i \in N}|y_i - \hat y_i| \\ acc(y, \hat y) = \sum_{i \in N}|y_i - \hat y_i|^2 \\ acc(y, \hat y) = \sum_{i \in N} \frac{|y_i - \hat{y_i}|}{|y_i|} acc(y,y^)=i∈N∑∣yi−y^i∣acc(y,y^)=i∈N∑∣yi−y^i∣2acc(y,y^)=i∈N∑∣yi∣∣yi−yi^∣
除此之外, regression问题里面有一个比较重要的评价方式叫做R2-scoree:
R 2 ( y , y ^ ) = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 R^2(y, \hat y) = 1 - \frac{\sum_{i=1}^n(y_i - \hat y_i)^2}{\sum_{i=1}^n(y_i - \bar y)^2} R2(y,y^)=1−∑i=1n(yi−yˉ)2∑i=1n(yi−y^i)2
- 第一种情况: 如果所有的y_i和yhat_i的值都相等, 那么R2(y, yhat) = 1
- 第二种情况: 如果所有的yhat_i是y_i的平均值, 那么R2(y, yhat) = 0
- 第三种情况: 如果R2的值比0还小, 就意味着它还不如我们做统计求平均值,瞎猜的结果. 也就是连baseline都没达到.
R2-scoree之所以常常会被用于进行回归问题的评测, 主要的原因就是它防止了机器作弊.
比方说我们现在有一组数据, 这组数据实际都是0.99, 0.97, 0.98…, 这些数字都很小, 而且都很密集. 那么给机器使用的时候随便做一个平均值, 感觉到准确度还挺高, 那就被骗了.
F-score
在precision和recall之外, 还有一个比较重要的内容, 叫做F-score.
首先我们要知道, precision和recall这两个值在实际工作中往往是相互冲突的. 为了做个均衡, 就有了F-score.
F − s c o r e = ( 1 + β 2 ) ∗ p r e c i s i o n × r e c a l l β 2 ∗ p r e c i s i o n + r e c a l l \begin{align*} F-score & = \frac{(1+\beta^2) * precision \times recall}{\beta^2 * precision + recall} \end{align*} F−score=β2∗precision+recall(1+β2)∗precision×recall
β \beta β是自行定义的参数,由这个式子可见F-score能同时考虑precision和recall这两种数值。分子为precision和recall相乘,根据式子,只要precision或recall趋近于0,F-score就会趋近于0,代表着这个算法的精确度非常低。一个好的算法,最好能够平衡recall和precision,且尽量让两种指标都很高。所以有一套判断方式可以同时考虑recall和precision。当 β → 0 \beta \to 0 β→0, F-score就会退化为precision, 反之, 当 β → ∞ \beta \to \infty β→∞, F-socre就会退化为recall.
我们一般说起来, F-score没有特别定义的话, 就是说 β \beta β为1, 一般我们写成F1-score.
F 1 − s c o r e = 2 × p r e c i s i o n × r e c a l l p r e c i s i o n + r e c a l l \begin{align*} F1-score & = 2 \times \frac{precision \times recall}{precision + recall} \end{align*} F1−score=2×precision+recallprecision×recall
F1-score是仅当precision和recall都为1的时候,其值才等于1. 而如果这两个值中任意一个不为1时,其值都不能等于1. 也就是说,当2*1/2 = 1时, F1-score=100%, 代表该算法有着最佳的精确度.
AUC-ROC
除了F-score之外,还有比较重要的一个概念: AUC-ROC. 这个也是为了解决样本不均衡提出来的一个解决方案.
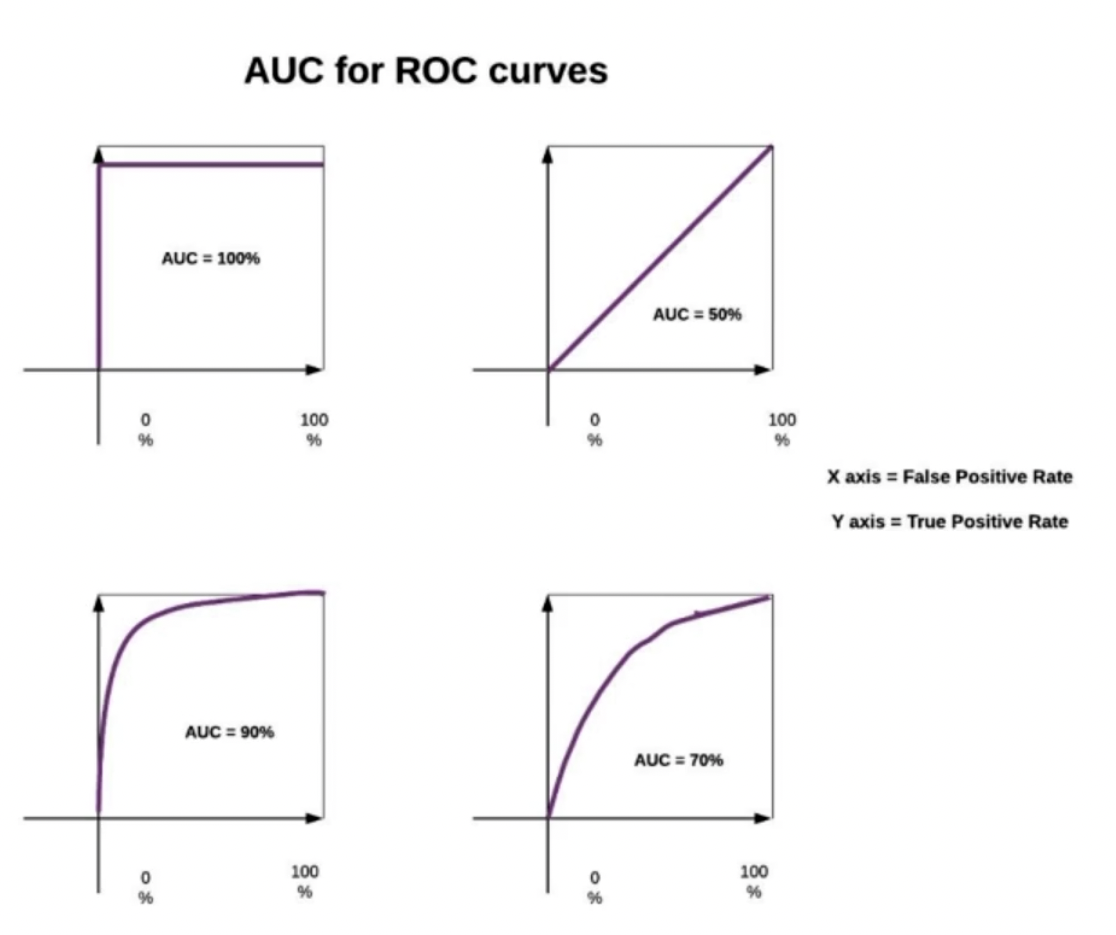
首先我们要先了解ROC曲线(receiveroperating characteristic), ROC曲线上的每一个点反映着对同一信号刺激的感受. AOC(Area under Curve), 是ROC曲线下的面积, 取值是在0.1 ~ 1 之间.
我们直接来看看,它在实际场景下是怎么用的.
还记得咱们在之前设定的阈值decision_boundary = 0.5, 我们就拿这个阈值来看. threshold:0.5. 在我们二分类问题中, 当预测值大于0.5的时候,也就等于1了. 也就是说,只要超过0.5, 我们就判定为positive值.
好,现在还是的请我们劳烦了无数次的警察a同志来帮帮我们. 当警察a去抓罪犯的时候,盘但一个人是不是犯了罪, 他的决策很重要. 在事实清晰之前,警察a的决策只有超过0.5的时候,才能判定这个人是positive,也就是罪犯. 这个时候呢,我们假设precision是0.7.
现在又需要警察b出场了, 这个警察b的threshold为0.1的时候, 其precision就为0.7. 也就是说,他预计出的值,只要大于0.1, 就判定为positive, 这种情况下, 警察b判定的precision为0.7.
别急,这次需要的演员有点多,所以,警察c登场了. 那么警察c的threshold为0.9. 也就是说,警察c比较谨慎, 只有非常确定的时候, 才能判定positive. 警察c的情况,判定的precision也是0.7.
好,现在我们来用脑子思考下, 这三个警察哪个警察能力最强?
必须是警察b最厉害.
就如我们上面的那四个坐标轴, X轴代表threshold, Y轴表实positive, 当threshold轴上的取值还很小的时候, positive已经很大了.那明显紫色线条和threshold轴圈住的区域面积越大, 这个面积就是越大越好.
这就是AUC for ROC curves, 这个主要就是为了解决那些样本及其不均衡的问题. 因为样本非常不均衡的时候, position和recall你有可能都会很低, 这个时候就不好对比. AUC曲线对于这种情况就比较好用一些.
其实在真实情况下, 绝大多数问题都不是很均衡的问题. 比方说预测病, 找消费者, 找高潜力用户. 换句话说, 如果高潜用户多就不用找了.
我们在研究ROC曲线实际应用的时候,依然会用到上面给大家所讲的tp, fp, fn, tn. 这里会引出另外两个东西, TPR和FPR, 如下:
T P R = t p t p + f n F P R = f p f p + t n \begin{align*} TPR & = \frac{tp}{tp+fn} \\ FPR & = \frac{fp}{fp+tn} \end{align*} TPRFPR=tp+fntp=fp+tnfp
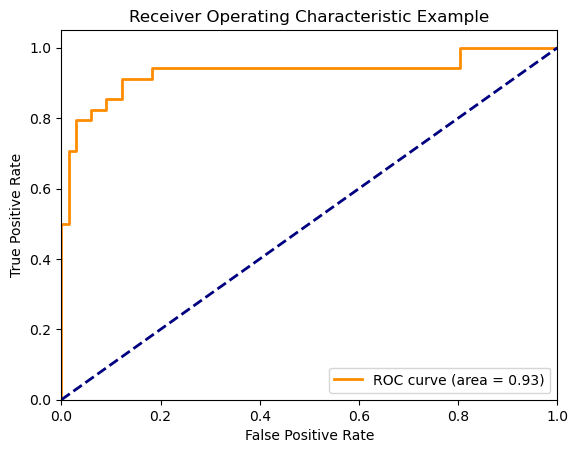
我们来看看咱们之前的这组数据的AUC值:
from sklearn.metrics import roc_curve, aucfpr, tpr, thresholds = roc_curve(true_labels, losses)roc_auc = auc(fpr, tpr)
print('AUC: {}'.format(roc_auc))---
AUC: 0.9300356506238858
下一节课,咱们来说一个非常重要的概念:拟合和欠拟合.









 — 训练机器学习模型用GPU还是NUP更有优势(基于文心一言的回答))

)







