一元函数极值问题

0 引言

在高等数学课程中，我们应该都学习过一元函数的极值问题，这篇文章我们再来回顾一下相关知识点。为什么要对一元函数的极值问题进行回顾？因为后面我会出一篇非线性规划问题的极值问题，其中会涉及到多元函数的极值，所以这篇文章的内容相当于是为后面文章做铺垫，也能够让读者进行对比理解！

1 定义

函数极值(Relative/Local Extrema)的定义：
若$\exists \delta >0$，使得：
$\forall x\in U(x_0,\delta )$，恒有$f(x)\ge f(x_0)$,则称$f(x)在x_0$处取得极小值；
$\forall x\in U(x_0,\delta )$，恒有$f(x)\ge f(x_0)$,则称$f(x)在x_0$处取得极大值。

上述的定义可解释为：
极大值(local/ relative maximum):某点附近的函数值都比该点的函数值小；
极小值(local/ relative minimum): 某点附近的函数值都比该点的函数值大。

函数的极值指的是函数在某点附近($U(x_0,\delta )$就是指$x_0$附近的区域)的最大值或者最小值，所以极值是函数局部的性质。

需要注意的，某点附近最大或者最小指的是必须比左右两边都大或者都小才能叫极值。如下图，图a是极大值，x=c处的值比它附近（附近可以理解为黑色圆圈范围）的值都大；图b是极的x=c处的值比它附近的值都小，因此为极小值；但是图c，x=c左边的值小于$f(c)$，右边的值大于$f(c)$，不满足极值的定义，图d也是如此。

2 极值与最值

再来介绍一下最值，最值分为最大值(global maximum, absolute maximum)以及最小值(global minimum, absolute maximum)，与极值不同的是，最值是函数全局的性质，它不是某点附近，而是函数整个定义域中的最大值和最小值。
那函数的极值和最值，有什么关系呢？其实极值和最值之间没有很强的关系，最值点可能是也可能不是极值点，极值点也可能是也可能不是最值点。如下图所示，最大值点不是极值点，最小值点时极值点，极大值点不是最大值点，极小值点也不是最小值点。
最重要的是清楚两者的概念，以及极值是局部的特性，最值是全局的特性。

3 极值的判定方法

高数中对于一元函数的极值主要有三种判定方法

• 法一：通过上述定义判定
• 法二：通过函数一阶导判断
  设$f^{{}^{\prime }}(x_0)=0$，且$f(x)$在$x_0$的邻域内可导，则
  极小值点：$x_0$的左边，$f^{{}^{\prime }}(x_0)<0$，$x_0$的右边，$f^{{}^{\prime }}(x_0)>0$;
  极大值点：$x_0$的左边，$f^{{}^{\prime }}(x_0)>0$，$x_0$的右边，$f^{{}^{\prime }}(x_0)<0$。
• 法三：通过函数二阶导判断
  设f(x)在$x_0$处二阶可导，且$f^{{}^{\prime }}(x_0)=0$，$f^{{}^{\prime \prime }}(x_0)\ne 0$，则 :
  极小值点：$f^{{}^{\prime \prime }}(x_0)>0$
  极大值点：$f^{{}^{\prime \prime }}(x_0)<0$

4 驻点与极值点

在学高数的时候，我们知道对于一元函数，一阶导为0的点即$dy/dx=0$的点称为驻点，那极值点和驻点有什么关系呢？

1. 极值点不一定是驻点
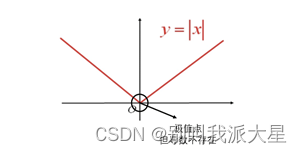
   比如$f(x)=|x|$，x=0是该函数的极值点，但不是驻点。
   解释一下为什么不是驻点：驻点是一阶导为0的点，前提是一阶导要存在，但是该函数在x=0处，左导数存在，右导数存在，但是左导数≠右导数，所以导数不存在。进一步的，介绍一个概念：函数在该点左右侧导数存在且有限，但不相等的点称为角点。很形象，也很好理解，左右导数不相等，说明曲线在该点不平滑，出现了凸出来的角，所以叫做角点。所以$f(x)=|x|$在x=0处就是一个角点，导数不存在。
   

2. 驻点也不一定是极值点
   比如$f(x)=x^3$，其一阶导为$f^{{}^{\prime }}(x)=x^2$，$x=0$时,$f^{{}^{\prime }}(0)=0$,因此x=0是函数$f(x)=x^3$的驻点，但根据上面所述的极值点判定方法或者根据图像去判断，可以发现x=0并不是该函数的极值点。

所以，对于一元函数，极值点不一定是驻点，驻点也不一定是极值点！
当然，如果给定条件，f(x)连续可导，那么极值点一定是驻点！

然而，在非线性规划问题中，我们所遇到的函数往往都是多元函数，所以我会在下一篇文章中进一步介绍具有一般性的多元函数的极值。