习题链接：幸运的袋子_牛客题霸_牛客网

题目分析

 由题意可知：“幸运的袋子”的概念是——小球的数值之和大于小球的数值之积。

假如现在有5个小球：1，1，3，5，7，并将他们编号a0~a4.我们现在来看其中一种满足“幸运”条件的情况：我们设置变量sum来记录数值之和，用multi来记录数值之积，用count来记录袋子数量。

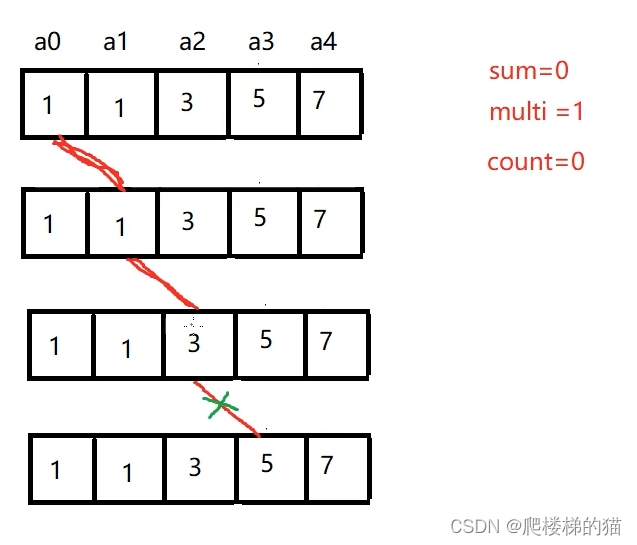
 我们先取a0这个小球，数值为1。接着取a1——（1+1）>（1*1），满足条件，计数器count+1.我们继续取a2——（1+1+3）>（1*1*3），满足条件，计数器count+1.

接着我们取a3，（1+1+3+5+7）<（1*1*3*5*7）,不满足条件。那么我们就要回到上一层（取a2的那一层）来试试下一个取a4是否满足要求。

但是此时sum = (1+1+3+5+7) = 17，multi = 105,要想回到上一层就得sum减去刚拿到的a3，multi除以刚乘上的a3.然后去取a4，看看是否满足条件。

但是因为我们对数字进行递增排序了，如果a3不满足条件，那么a4也不会满足。

最后返回count的值。

---

如果我们写一个count函数，用来获得从取得某个球开始的“幸运袋子”的个数。对于n个小球来说，自小球a0开始的袋子个数为：小球a0与下一个小球ax之间袋子的个数 加上 以小球ax开始与ax的下一个小球之间的袋子个数 之和。然后依次递归

那么回到一个小球也没取的时候，此时为空（什么也没有），那么袋子的个数是不是 取第一个小球的个数（此时你取哪个小球都满足要求，因为此时就一个小球）加上 第一个小球与其取得下一个小球所有可能？

很好，现在我们总结出了其中的规律，现在我们来写代码

---

import java.util.*;
public class FortunatePackage {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();//输入小球的个数int[] a = new int[n];//将所有小球放入一个数组中，以数组下标为小球编号for (int i = 0; i < n; i++) {a[i] = sc.nextInt();}Arrays.sort(a);//将小球递增排序，以节省算力/*为什么要排序？仍然以（1，1，3，5，7）为例，当取到5时，5不满足要求，那么它后面的数都比它大，也一定不满足要求了*/System.out.println(count(a, n, 0, 0, 1));//从第一个下标开始取小球}/*pos是查找“幸运袋子”时的“第一个球的位置”，a[]是目前可供挑选的球，sum为和（初始值为0），multi为积（初始值为1），n为球的个数*/public static int count(int[] a,int n,int pos,int sum,int multi){int count = 0;for (int i = pos; i < n; i++) {sum += a[i];multi *= a[i];//如果这两个球满足“幸运袋子”的要求，“幸运袋子”的组合种类数为 1（这两个球组成的袋子）+ 剩下的所有球中存在的“幸运袋子”数if (sum > multi){count = count + 1 + count(a,n,i+1,sum,multi);}else if (a[i] == 1){count = count + count(a,n,i+1,sum,multi);}else {break;}//如果这两个球不满足“幸运袋子”的要求，则清除此次操作带来的数据改变，回溯到上一层sum -= a[i];multi /= a[i];//如果这个球不满足要求并且和下一个球的数值相等，则跳过下一个球的检测while (i < n-1 && a[i] == a[i+1]){i++;}}return count;}
}