上一节已知，任意的协向量都可以写成对偶基向量的线性组合，以及如何通过计算基向量穿过的协向量线来获得协向量分量，且看到 协向量分量 以 与向量分量 相反的方式进行变换。
现要在数学上确认协向量变换规则是什么。
第一件事：弄清协向量本身是怎么转换的，
使用向量以便从旧基中获取新基，用旧基构建新基，这就是前向变换，
现对协向量也同样如此，
这里的Q是多少呢？？？
为计算出Q，
首先将与e1进行相乘， 即
该方程的左右两边同时右乘e1，
得到：
而, 故有：
类似的，
于是得到：
鉴于此，进行 后向转换。 以便可根据新的基向量写出旧的基向量。
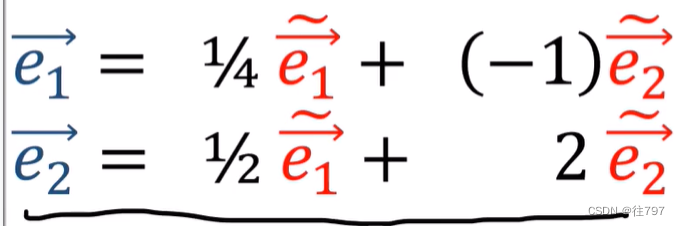
把 这两个方程 代入到上面 那个方程。
于是我们就能得到，如何通过旧的对偶基向量， 表达新的对偶基向量，
同样的道理，可以通过该方式，计算得到：
对比系数：
这意味着，从旧的对偶基向量 到 新的对偶基向量，可以使用 后向转换。
接下来，尝试证明对于所有维度：
前提设置：
双基的定义：
前向转换 和 后向转换（Forward、 Backward）：
另外，前向转换和后向转换是互逆的：
开始
当 j ≠ l 时，， 故
可以用
代替，
理解：
中的l全部代入， 当 j ≠ l 时，
，仅
，1省略不写，
变为
，再结束l这个求和项。
得到的最后一个式子，最后一个式子的左边就是一个单位阵E，即右边两个东西互逆，而F与B又是互逆的，等量代换，。
所以，就是使用反向转换（Backward）使得 从旧对偶基 到 新对偶基。
现在，就可以明白为什么视频的老师 把协向量的索引 写在顶部， 因为它们的变换与基向量的方式相反。
基向量 和 协向量 的变换规则 总结：
现已知 基向量的转换方式， 想弄清它们的分量如何转换就比较容易，
将某一协向量α写成 旧基协向量的线性组合，
将最后一个等式 与 上面那个线性组合进行比较，
同样地，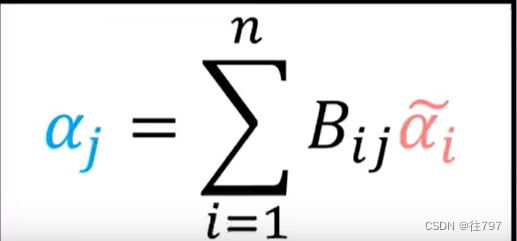
注意，是以向量那个为本，其他的转换方式都与向量的来进行比较， 反就弄上标，同就下标。
Contravariant---逆变的，反变的。
Covariant 协变的，共变式。
