前言
Softmax函数
SoftMax ( x ) i = e x i e x 1 + ∑ j = 2 N e x j , x 1 ≫ x j , j ∈ 2 , … , N \text{SoftMax}(x)_i = \frac{e^{x_i}}{e^{x_1} + \sum_{j=2}^{N} e^{x_j}}, \quad x_1 \gg x_j, j \in 2, \dots, N SoftMax(x)i=ex1+∑j=2Nexjexi,x1≫xj,j∈2,…,N
Softmax 通常用于多类别分类问题中的输出层。在这个公式中,给定一个输入向量 ( x = [ x 1 , x 2 , … , x N ] x = [x_1, x_2, \ldots, x_N] x=[x1,x2,…,xN] ),Softmax 函数将其转化为一个概率分布 ($ p = [p_1, p_2, \ldots, p_N]$ )。每个元素 $p_i KaTeX parse error: Can't use function '\(' in math mode at position 10: 表示该样本属于第 \̲(̲ i KaTeX parse error: Can't use function '\)' in math mode at position 1: \̲)̲ 类的概率。 e^{x_i}$ 表示输入向量中第 ($ i $) 个元素的指数,而分母部分是所有元素的指数之和。这样的设计确保了输出概率分布的归一性,因为指数函数的性质使得所有元素都为正数,而分母的和则确保了概率总和为 1。
当 x 1 ≫ x j , j ∈ 2 , … , N x_1 \gg x_j, j \in 2, \ldots, N x1≫xj,j∈2,…,N 时,输入向量的第一个元素 x 1 x_1 x1 往往会远远大于其他元素,这可以帮助模型在分类时更明确地选择一个主要的类别。
attention sink
文中提到:语言模型(LLMs)在注意力机制中存在过度关注初始令牌(initial tokens)的现象。从以下两个角度探索下。
softmax角度
在SoftMax函数中, e x i e^{x_i} exi是指数函数,这意味着即使输入的初始令牌 ( x 1 x_1 x1) 在语义上与语言建模不相关,由于指数函数的存在,SoftMax 函数的输出中它仍然会有一个非零的值。因此,模型在进行自注意力机制时,即使当前的嵌入已经包含了足够的自包含信息用于预测,模型仍然需要从其他头和层中的其他令牌中汇聚一些信息。结果,模型倾向于将不必要的注意力值“倾泻”到特定的令牌上,这就是所谓的attention sink(注意力汇聚)。
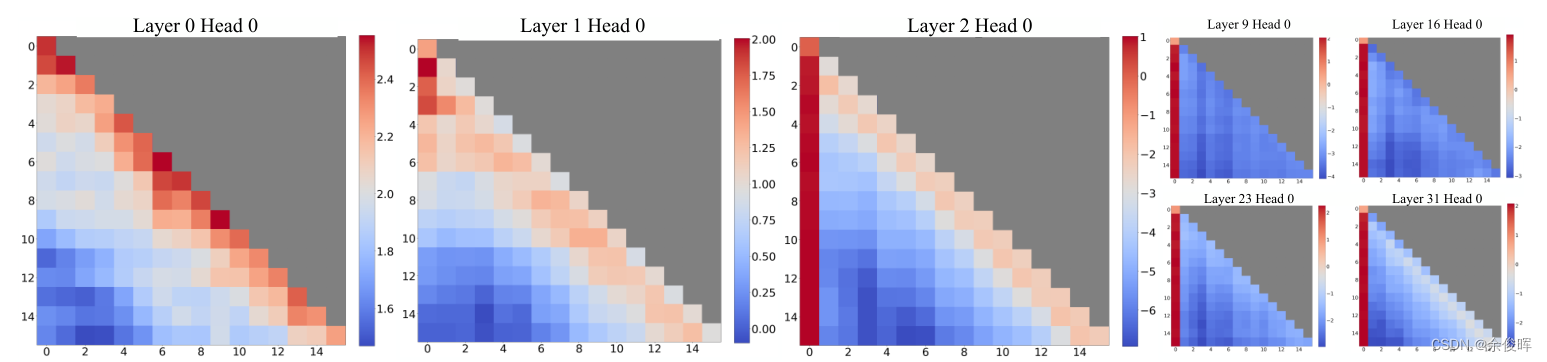
- 局部模式在前两层中的呈现: 在第一层和第二层(layers 0 和 1),注意力图呈现出“局部”模式,即对最近的令牌给予更多的关注。这表明模型在初步的处理阶段更注重周围的令牌,强调了局部上下文的重要性。
- 模型跨所有层和头部(heads)都强烈关注初始令牌: 在底部两层之外,也就是深层网络中,模型在所有层和头部都倾向于强烈关注初始令牌。这与“attention sink”现象相吻合,即模型在处理过程中过度关注初始令牌,而 SoftMax 函数的特性是导致这种现象的原因之一。
自回归模型角度
由于自回归语言建模的顺序性质,初始令牌对所有后续令牌都是可见的,而后续令牌只对一组有限的后续令牌可见。因此,初始令牌更容易被训练成注意力的聚焦点,捕捉到不必要的关注(在训练中可能导致模型过度集中注意力,捕捉到一些在语言建模任务中并不重要的信息。)。如何理解呢?
-
自回归性质: 这些模型是自回归的,即它们根据之前生成的令牌来生成下一个令牌。在这个过程中,初始令牌是最早生成的令牌,因此在生成整个序列的过程中,它对所有后续令牌都是可见的。
-
可见性的不对称性: 由于模型是按顺序生成令牌的,初始令牌在生成序列的整个过程中一直是可见的,而后续令牌只能被生成的一小部分令牌所看到。这种不对称性导致了对初始令牌更强烈的关注。
-
训练中的注意力聚焦点: 由于模型在训练过程中学会了将注意力集中在初始令牌上,这些令牌更容易成为“attention sink”,即吸引不必要的注意力。这可能是因为初始令牌在训练中更频繁地与后续令牌发生交互,从而更容易捕捉到一些模型认为重要的信息。
sink token
Q:如何卸载模型过度关注初始令牌的注意力得分?
A:引入一个专门的“汇聚标记(可学习的占位符令牌)”(sink token)来卸载过多的注意力得分。由于这一点,模型无意中将全局可见的令牌,主要是初始令牌,作为注意力的聚焦点。提出的潜在解决方案有两个:
-
引入全局可训练的注意力汇聚标记(Sink Token): 有意地引入一个全局可训练的注意力汇聚标记,即“Sink Token”。这个标记的作用是作为一个储存不必要注意力分数的仓库。通过这种方式,模型可以有一个指定的位置,用于处理额外的注意力,避免过度关注全局可见的令牌,特别是初始令牌。
-
替代传统的 SoftMax 函数: 用 变体函数( S o f t M a x 1 SoftMax_1 SoftMax1 )替代传统的 SoftMax 函数。变体的公式如下:
SoftMax 1 ( x ) i = e x i 1 + ∑ j = 1 N e x j \text{SoftMax}_1(x)_i = \frac{e^{x_i}}{1+\sum_{j=1}^{N} e^{x_j}} SoftMax1(x)i=1+∑j=1Nexjexi
与传统的 SoftMax 不同, S o f t M a x 1 SoftMax_1 SoftMax1 不要求所有上下文令牌的注意力分数总和为一(具体而言: S o f t M a x 1 SoftMax_1 SoftMax1 通过修改分母中的求和项,使其不再求和到所有元素,而是到 ( N N N)(元素总数)前一个元素。具体而言,公式中的 ( 1 + ∑ j = 1 N e x j 1+\sum_{j=1}^{N} e^{x_j} 1+∑j=1Nexj) 不再求和到 ( j = N j=N j=N),而是求和到 ( j = N − 1 j=N-1 j=N−1)。)。那么这种修改有什么效果?-
减缓数值爆炸的风险: 通过避免对所有元素的指数求和, S o f t M a x 1 SoftMax_1 SoftMax1在一定程度上减缓了数值爆炸的风险,使模型在数值上更加稳定。
-
降低对其他元素的依赖: 这个修改使得最大的元素不再对分母的求和贡献,减少了其他元素相对于最大元素的影响,使模型对其他元素的变化更为鲁棒。
这种变体可能也是一种有效的解决方案。文中将其标记为“Zero Sink”,因为它相当于在注意力计算中使用具有全零关键(Key)和值(Value)特征的令牌。
-

这些可视化结果基于 256 个句子,每个句子包含 16 个令牌。左边是使用 Sink Token 的模型,右边是没有使用 Sink Token 的模型。两个图表显示相同的层次和头部。
-
没有 Sink Token 的情况: 在没有 Sink Token 的模型中,底层显示出局部关注,而在更深层次上,模型更加关注初始令牌。即模型容易在深层次上过度集中注意力在初始令牌上。
-
有 Sink Token 的情况: 在有 Sink Token 的模型中,可以清晰地看到在所有层次上都有关注它的明显现象,有效地聚集冗余的注意力。这表明 Sink Token 成功地成为一个注意力的集中点。
-
有 Sink Token 时对其他初始令牌的关注减少: 在存在 Sink Token 的情况下,相对较少的注意力被分配给其他初始令牌,支持了将 Sink Token 指定为提高流式性能的设计优势。
总结
本文介绍了关于 StreamingLLM中提到的关于attention sinks和sink token的原理。在原文中提到,通过引入“attention sinks”与最近的令牌配对,能够高效地处理长度达 4 百万令牌的文本。还通过使用具有专门的 sink token 的预训练模型,以此提高流式应用部署的性能。
更多实验细节有兴趣关注原文。
参考文献
【1】Efficient Streaming Language Models with Attention Sinks,https://arxiv.org/abs/2309.17453
【2】code:https://github.com/mit-han-lab/streaming-llm



)















