系列文章目录
第一章 Python 机器学习入门之线性回归
第一章 Python 机器学习入门之梯度下降法
第一章 Python 机器学习入门之牛顿法
第二章 Python 机器学习入门之逻辑回归
逻辑回归
- 系列文章目录
- 前言
- 一、逻辑回归简介
- 二、逻辑回归推导
- 1、问题
- 2、Sigmoid函数
- 3、目标函数
- 3.1 让步比
- 3.2 极大似然估计
- 3.3 推导
- 4、代价函数
- 5、最大化似然函数
- 三、逻辑回归实现
- 结果展示
前言
第二次实验开始了,内容是逻辑回归,听起来像是线性回归的兄弟,然而仔细查阅后发现逻辑回归其实是一种分类算法;
我们知道回归算法的结果建立在连续的数据上,分类算法的结果建立在离散的数据上;因此逻辑回归本质上是一种分类算法,那问题就来了,一个分类算法为啥叫回归呢?

一、逻辑回归简介
百科定义:
logistic回归又称logistic回归分析,是一种广义的线性回归分析模型,常用于数据挖掘,疾病自动诊断,经济预测等领域。
简单来说,逻辑回归还是建立在我们之前学习的线性回归模型基础上,使用回归的方法来实现分类的目的;就好像同在一个专业学习,有些人学习计算机是为了成为一个优秀的程序员,有些人学计算机是为了挑选出优秀的程序员,结果不一样但在过程中是有很多的相似之处的。
二、逻辑回归推导
1、问题
假设你是一个大学系的管理员,你想根据两个考试的结果确定每个申请人的录取机会。您可以将以前申请者的历史数据用作逻辑回归的培训集。对于每个培训示例,您都有申请人的两次考试成绩和录取决定。为了实现这一点,我们将建立一个分类模型,根据考试成绩估计入学概率。(取自吴恩达机器学习中文版课后题)
先来分析一下,如果我们现在使用线性回归模型来分析该该题,我们最后得出的结论应该是根据考试成绩来预测入学成绩,但是现在结果需要我们来判断是否能成功入学,那我们就在此基础上对之前的入学成绩设定阈值,根据该阈值对结果进行分类来选择是否录取;
但是线性回归模型往往是一条斜线,如何满足结果不是0就是1呢?因此我们引入了Sigmoid函数。
2、Sigmoid函数
先看一下线性回归模型假设函数
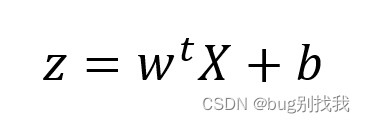
sigmoid函数公式如下
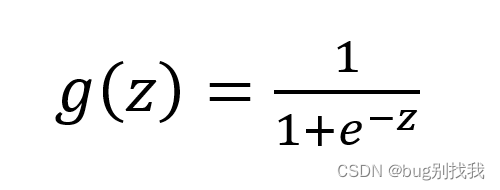
将线性回归模型的预测值视为上式的自变量z,可得出下图结果
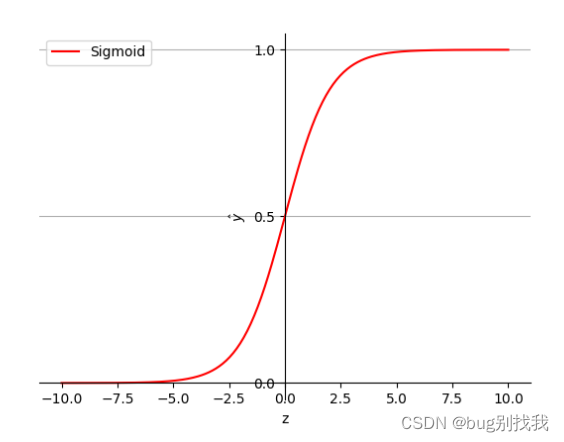
然而上图结果仍然不是我们真正需要的结果,我们需要的是一个二元离散模型,结果非1即0,因此我们还需处理一下,根据与阈值的差值判断结果
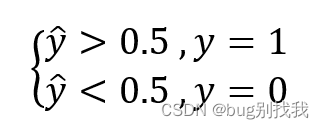
当y ̂ ==0.5时,我们根据实际情况来定;同时上面的阈值是我们手动设置的(并不一定需要0.5),依情况而定,这也是逻辑回归模型的优势之一
3、目标函数
在上面的sigmiod函数上我们建立了逻辑回归的假设函数,我们想要得到它的目标函数,首先得知道自变量X和结果变量y之间的关系,因此我们引入两个概念让步比和极大似然估计
3.1 让步比
让步比可以理解成有利于某一特定事件的概率,如下

3.2 极大似然估计
思想:如果一个事件发生了,那么发生这个事件的概率就是最大的;对于样本i,其类别为
y ̂ ∈(0,1),对于样本i,可以把h(Xi)看成是一种概率;yi对应是1时,概率是h(Xi)(即Xi属于1的概率,即p(Y=1|X));yi对应是0时,概率是1-h(Xi)(Xi属于0的概率,即p(Y=0|X)
已知下式
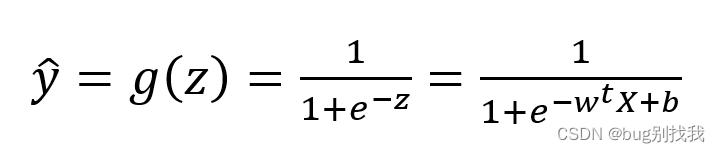
在这里使用极大似然估计做一个假设,假设y ̂ 为样本x为正例的概率,那么1-y ̂ 为样本x为负例的概率
在此基础上我们可以将让步比的对数形式转成特征值相关式子;
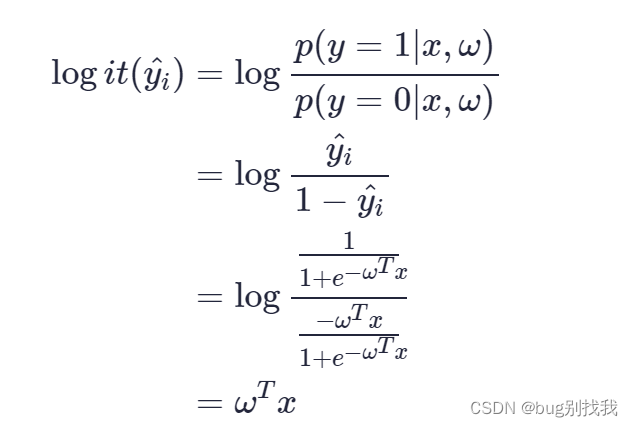
然而我们更想要的是预测值和它发生的概率之间的关系,即让步比之间的逆形式
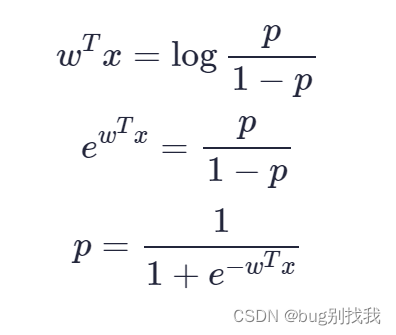
3.3 推导
已知样本X结果分类的概率
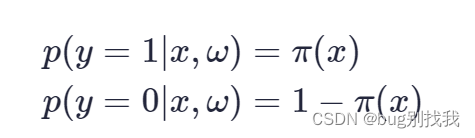
将上式联系得y的概念分布函数
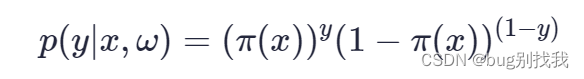
通过y的概率分布函数表达式即可得似然函数为(m为样本数量)
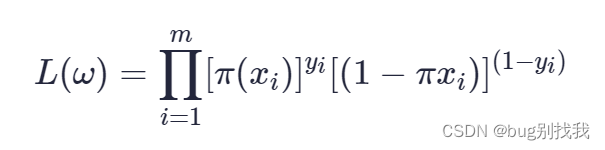
通过似然函数得到对数似然函数即目标函数
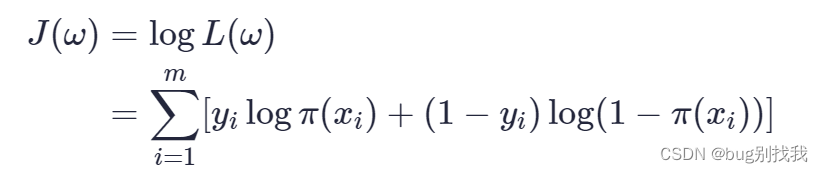
4、代价函数
对于二分类问题,分别考虑y=1和y=0的情况
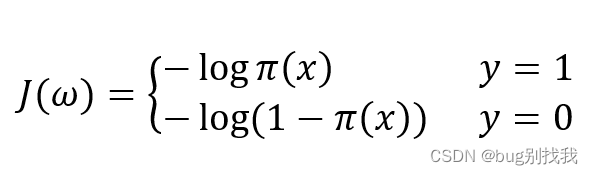
5、最大化似然函数
最大似然估计是似然函数最初也是最自然的应用,似然函数取得最大值表示相应的参数能够使得统计模型最为合理;
可以使用梯度上升法和牛顿法两种优化方法,这里说一下梯度上升法,本质和之前的梯度下降原理一一样,展开一阶梯度来求最优解;先求目标函数对参数w的偏导
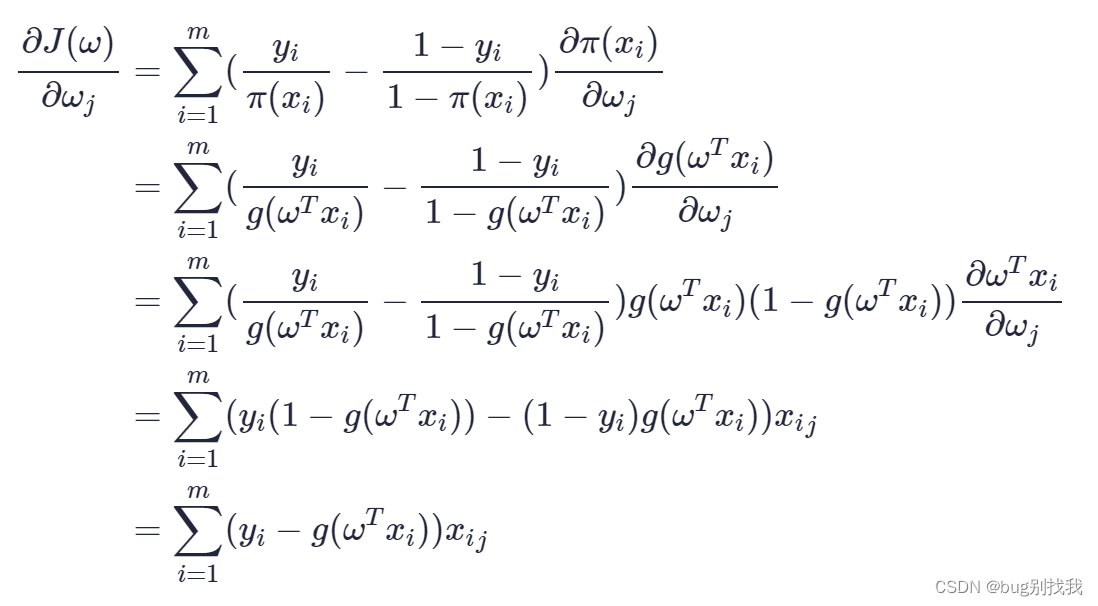
因此逻辑回归模型的梯度下降函数如下,wj代表第j个模型参数
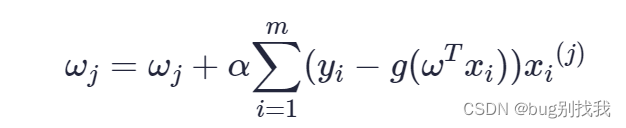
三、逻辑回归实现
结果展示