思路

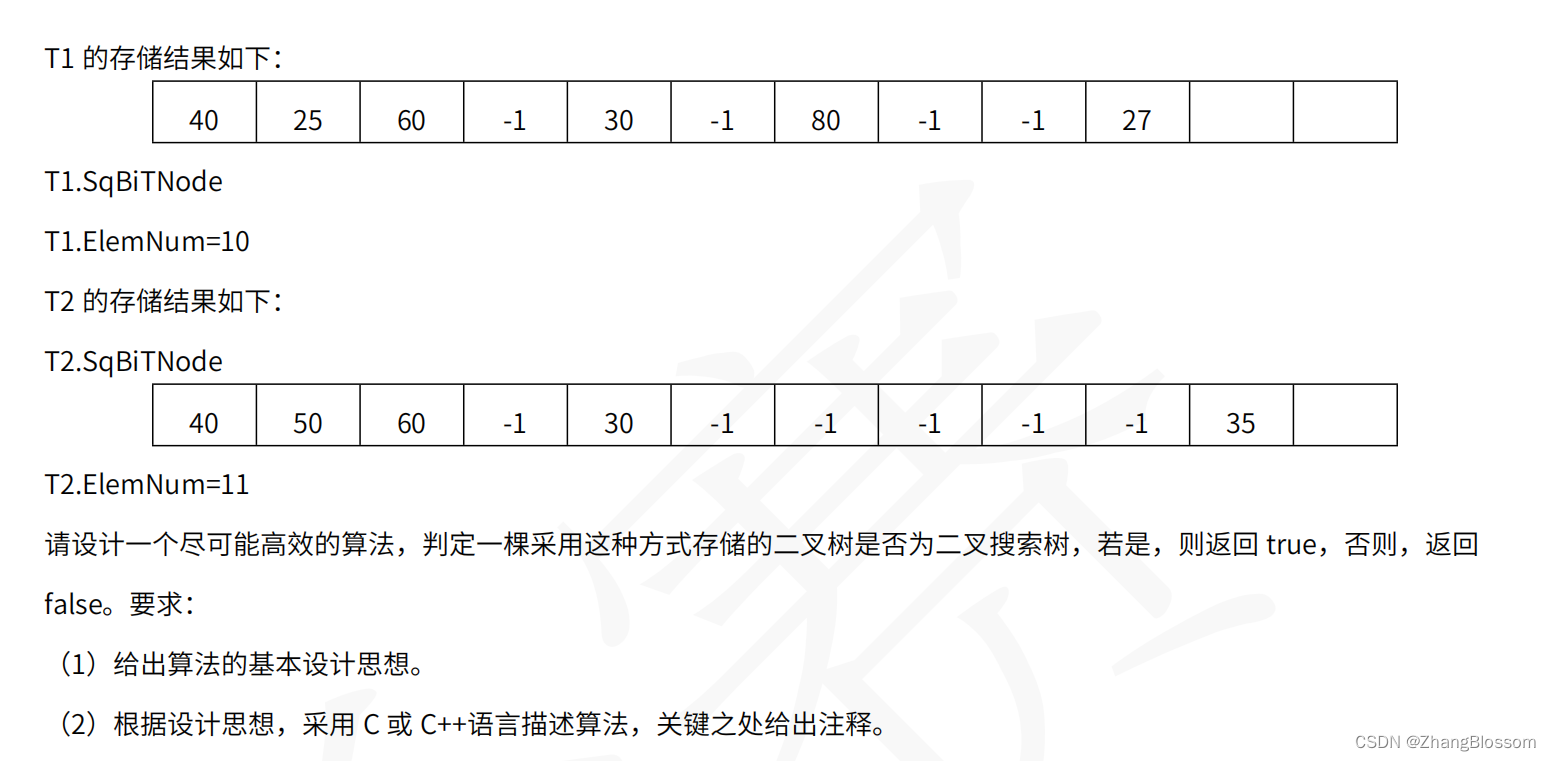
很明显，这是一个顺序存储结构的树的构成方法。其中树的根节点位置从索引0开始，对于该结构，存在有：如果当前根节点的下标为n，那么其左子树下标为2n+1，右子树下标为2n+2。
而对于BST，我们知道，其一个非常显著的特点就是：对于根节点root，其左子树小于其根节点的值，其右子树大于其根节点的值。同时，如果当前节点为null，不影响其是否为BST。
基于这个理论，我们大概的实现思路是：递归的判断当前根节点的左子树和右子树，并且限定其左右子树的值的大小区间范围。
那么这里应该如何去限制这个范围呢？
从上面的理论中我们可以得到如下的伪代码：

//如下代码基于链式存储结构 不过不影响理论实践
bool isBST(SqBiTree* root,int low,int high)
{if(root==null){return true;}//这里逻辑严谨应该增加一个左右指针的非空判断 我就不写了if(root.left.val>=root.val || root.right.val <= root.val){return false;}return isBST(root.left,low,root.val) && isBST(root.right,root.val,maxValue);
}

为什么要这么写呢？
首先我们基于上面的定义，如果当前节点为空，不影响当前树是否是BST，因此直接返回tree。
之后，我们开始条件判断，当前节点的左右子节点，是否小于和大于当前节点。
如果不是，也就是违法了BST的特性，那么我们直接返回false。
并且，我们一开始也说了，这应该是一个递归的判断过程，因此我们还需要对当前root节点的左子树和右子树继续去执行当前的递归过程。
那么递归的条件是什么？
对于当前节点的左子树，其最小值应该是不限定的，但是其最大值必须小于当前节点的值，
而对于其右子树，其最小值应该大于当前节点的值，其最大值不限。
所以就可以得到最后两行代码的条件了。
那么换到我们题目中，我们只需要将指针操作，修改为对数组下标的数据判断即可。
最终就可以得到如下代码：

// 递归函数，判断以n为根的二叉树是否是BST
bool isBSTUtil(BinaryTree *T, int n, TreeNodeType minVal, TreeNodeType maxVal)
{if (T->data[n] == '\0')return true;TreeNodeType nodeValue = T->data[n];// 检查当前节点的值是否在[minVal, maxVal]的范围内if ((nodeValue <= minVal) || ( maxVal <= nodeValue))return false;// 递归检查左子树和右子树，更新范围return isBSTUtil(T, 2 * n, minVal, nodeValue) && isBSTUtil(T, 2 * n + 1, nodeValue, maxVal);
}

ok，经过上面的解释，我们就已经得到了完整的当前题目的实现思路了。
完整代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <math.h>#define MaxSize 100typedef int TreeNodeType;// 二叉树结构
typedef struct
{TreeNodeType data[MaxSize];int BiTreeNum;
} BinaryTree;// 声明队列数据结构
typedef struct
{int front, rear;int size;int capacity;int *array;
} Queue;void initTree(BinaryTree *T);
void createTree(BinaryTree *T, int n);
TreeNodeType rootTree(BinaryTree *T);
int countTree(BinaryTree *T);
int maxDepthOfTree(BinaryTree *T, int n);
void preOrderTraverse(BinaryTree *T, int n);
void inOrderTraverse(BinaryTree *T, int n);
void postOrderTraverse(BinaryTree *T, int n);
void levelOrderTraverse(BinaryTree *T); // 层序遍历
bool destoryTree(BinaryTree *T);
void traverseArray(BinaryTree *T); // 遍历数组
bool isBSTUtil(BinaryTree *T, int n, TreeNodeType minVal, TreeNodeType maxVal);// 队列相关函数
Queue *createQueue(int capacity);
bool isQueueEmpty(Queue *queue);
bool isQueueFull(Queue *queue);
void enqueue(Queue *queue, int item);
int dequeue(Queue *queue);int main()
{BinaryTree T;// 开始构造二叉树 其中使用1作为根节点下标// 而不是使用0，使用0的问题在于不好表示数据在数组中的位置// 我们知道二叉树满足 当前节点n的左子树和右子树的序列号应该为 2n和2n+1initTree(&T);printf("请输入根结点(输入#表示该结点为空):");createTree(&T, 1);traverseArray(&T);printf("当前二叉树的最大深度为：%d\n", maxDepthOfTree(&T, 1));printf("先序遍历：");preOrderTraverse(&T, 1);printf("\n");printf("中序遍历：");inOrderTraverse(&T, 1);printf("\n");printf("后序遍历：");postOrderTraverse(&T, 1);printf("\n");printf("层序遍历：");levelOrderTraverse(&T);printf("\n");if (isBSTUtil(&T, 1, -10000, 10000)){printf("this is a BST");}else{printf("this is not a BST");}return 0;
}void initTree(BinaryTree *T)
{int i;for (i = 0; i < MaxSize; ++i){T->data[i] = '\0';}T->BiTreeNum = 0;return;
}void createTree(BinaryTree *T, int n)
{char ch;// 刷新（清空）标准输入流（stdin）// 主打一个求稳fflush(stdin);// 输入当前节点信息 # 代表当前节点为空// 先构造过字数scanf(" %c", &ch);if (ch == '#'){ // 空直接返回return;}else{T->data[n] = ch;T->BiTreeNum++;printf("输入 %c 的左子树数据（输入#表示当前左子树为空: ", ch);// 这里有一个技巧createTree(T, 2 * n);printf("输入 %c 的右子树数据（输入#表示当前右边子树为空）: ", ch);createTree(T, (2 * n + 1));}
}// 计算二叉树的最大深度
// 从根节点到叶子节点的最长路径的长度
// 由于是顺序结构 因此这里从第一层也就是n=1开始向下遍历
// 然后不断的判断左子树和右子树的高度
// 最后取最大值
int maxDepthOfTree(BinaryTree *T, int n)
{if (n <= T->BiTreeNum && T->data[n] != '\0'){int leftDepth = maxDepthOfTree(T, 2 * n);int rightDepth = maxDepthOfTree(T, 2 * n + 1);return 1 + fmax(leftDepth, rightDepth);}else{return 0;}
}// 先序遍历 根左右
void preOrderTraverse(BinaryTree *T, int n)
{if (T->data[n] == '\0')return;else{printf("%c ", T->data[n]);preOrderTraverse(T, 2 * n);preOrderTraverse(T, (2 * n + 1));}
}
// 中序遍历 左根由7
void inOrderTraverse(BinaryTree *T, int n)
{if (T->data[n] == '\0')return;else{inOrderTraverse(T, 2 * n);printf("%c ", T->data[n]);inOrderTraverse(T, (2 * n + 1));}
}
// 后序遍历  左右根
void postOrderTraverse(BinaryTree *T, int n)
{if (T->data[n] == '\0')return;else{postOrderTraverse(T, 2 * n);postOrderTraverse(T, (2 * n + 1));printf("%c ", T->data[n]);}
}
void traverseArray(BinaryTree *T)
{for (int i = 1; i <= T->BiTreeNum; i++){printf("%c  ", T->data[i]);}printf("\n");
}// 层序遍历二叉树
void levelOrderTraverse(BinaryTree *T)
{if (T->BiTreeNum == 0){printf("二叉树为空\n");return;}Queue *queue = createQueue(T->BiTreeNum);int current = 1; // 从根节点开始while (current <= T->BiTreeNum){printf("%c ", T->data[current]);if (2 * current <= T->BiTreeNum && T->data[2 * current] != '\0'){enqueue(queue, 2 * current);}if (2 * current + 1 <= T->BiTreeNum && T->data[2 * current + 1] != '\0'){enqueue(queue, 2 * current + 1);}if (!isQueueEmpty(queue)){current = dequeue(queue);}else{break;}}free(queue->array);free(queue);
}// 创建队列
Queue *createQueue(int capacity)
{Queue *queue = (Queue *)malloc(sizeof(Queue));if (!queue){perror("内存分配失败");exit(EXIT_FAILURE);}queue->front = 0;queue->rear = -1;queue->size = 0;queue->capacity = capacity;queue->array = (int *)malloc(capacity * sizeof(int));if (!queue->array){perror("内存分配失败");exit(EXIT_FAILURE);}return queue;
}// 检查队列是否为空
bool isQueueEmpty(Queue *queue)
{return (queue->size == 0);
}// 检查队列是否已满
bool isQueueFull(Queue *queue)
{return (queue->size == queue->capacity);
}// 入队列
void enqueue(Queue *queue, int item)
{if (isQueueFull(queue)){printf("队列已满\n");return;}queue->rear = (queue->rear + 1) % queue->capacity;queue->array[queue->rear] = item;queue->size++;
}// 出队列
int dequeue(Queue *queue)
{if (isQueueEmpty(queue)){printf("队列为空\n");return -1;}int item = queue->array[queue->front];queue->front = (queue->front + 1) % queue->capacity;queue->size--;return item;
}// 递归函数，判断以n为根的二叉树是否是BST
bool isBSTUtil(BinaryTree *T, int n, TreeNodeType minVal, TreeNodeType maxVal)
{if (T->data[n] == '\0')return true;TreeNodeType nodeValue = T->data[n];// 检查当前节点的值是否在[minVal, maxVal]的范围内if ((nodeValue <= minVal) || ( maxVal <= nodeValue))return false;// 递归检查左子树和右子树，更新范围return isBSTUtil(T, 2 * n, minVal, nodeValue) && isBSTUtil(T, 2 * n + 1, nodeValue, maxVal);
}

408考研各数据结构C/C++代码（Continually updating）

408考研各数据结构C/C++代码（Continually updating）
这个模块是我应一些朋友的需求，希望我能开一个专栏，专门提供考研408中各种常用的数据结构的代码，并且希望我附上比较完整的注释以及提供用户输入功能，ok，fine，这个专栏会一直更新，直到我认为没有新的数据结构可以讲解了。
目前我比较熟悉的数据结构如下：
数组、链表、队列、栈、树、B/B+树、红黑树、Hash、图。
所以我会先有空更新出如下几个数据结构的代码，欢迎关注。 当然，在我前两年的博客中，对于链表、哈夫曼树等常用数据结构，我都提供了比较完整的详细的实现以及思路讲解，有兴趣可以去考古。