文章目录
- 算法原理
- 细节分析
- 优化1
- 优化2
- 算法复杂度分析
- 稳定性分析
- 总结
算法原理
冒泡排序(Bubble Sort) 就是从序列中的第一个元素开始,依次对相邻的两个元素进行比较,如果前一个元素大于后一个元素则交换它们的位置。如果前一个元素小于或等于后一个元素,则不交换它们;然后每一轮目前的元素中最大的或最小的排到最上面,就像水中的泡泡冒出来一样,故取名为冒泡排序

说简单点,就是比较两个相邻的元素,将值大或值小的元素交换到右边
动图演示如下

细节分析
冒泡排序中如果元素有N个,那么完成N-1趟即可. 以升序为例,因为每一趟都会将最大的元素排在最右边,当进行完N-1趟之后,那么剩下的那一个元素一定就是最小的,也一定在最左边,所以在完成N-1趟之后,排序也最终完成.
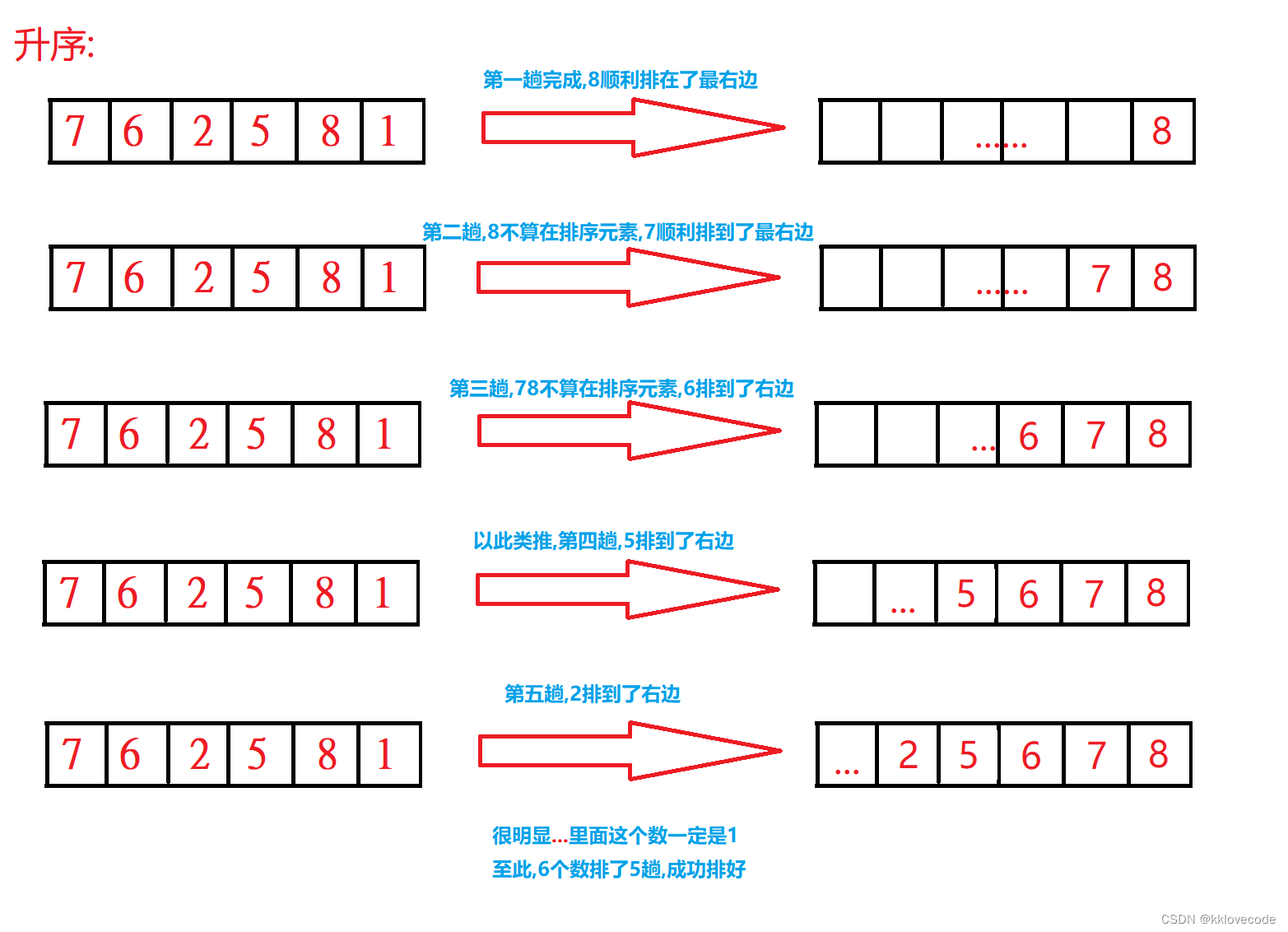
代码实现:
void bubble_sort(int* arr, int sz) //数组传的指针,参数中还需传递一个数组大小
{int i = 0;//趟数for (i = 0; i < sz - 1; i++) //总共趟数只有n-1趟{int j = 0;for (j = 0; j < sz - 1 - i; j++) //每轮里面排的数要依次递减{if (arr[j] > arr[j + 1]){int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}
优化1
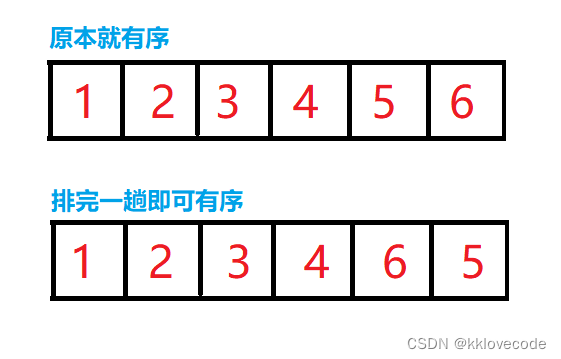
比如下图两种情况,当代码原本就已经是顺序排好的,或者在中途的时候顺便已经排好,但是你仍将按照上面代码一步一步运行,效率就会大打折扣
所以我们可以设立一个标志位,来提示我们是否排序是否已经排好,不用再进行优化
所以我们可以在代码中设立一个标志位,来提示我们排序是否已经排好,不用再进行优化
void bubble_sort(int* arr, int sz) //数组传递一定是指针
{int i = 0;//趟数for (i = 0; i < sz - 1; i++){int k = 1; //k就是一个标志位,在第一趟中如果k变成0了,就说明顺序是需要程序来排序的//如果k不变,还是等于1,则数据顺序本身就是好的,就直接breakfor (int j = 0; j < sz - 1 - i; j++){if (arr[j] > arr[j + 1]){int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;k = 0;}}if (k == 1){break;}}
}
优化2
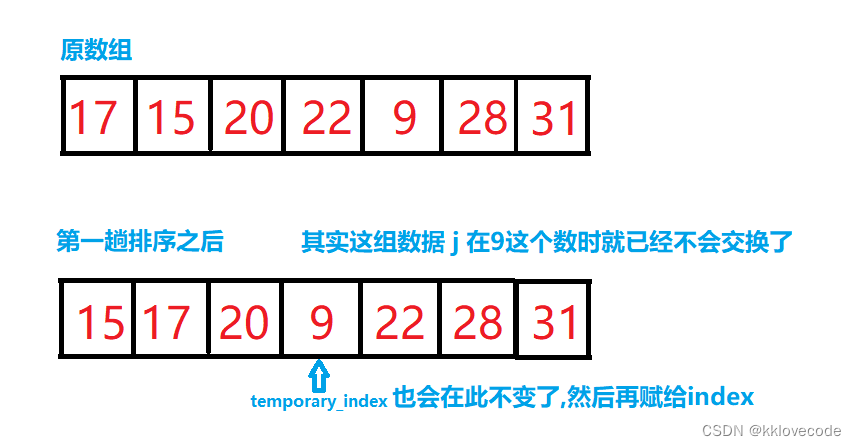
然而这种优化只能做到某一次排好序的时候我们直接退出排序以达到这个节约时间的要求,所以我们可以继续优化,当一个数组接近有序时(特别是有一小部分已经有序)我们往往只需要在某一个小范围内排序即可,我们可以用一个标记来表示这个范围的下限,例如遇到下面的情况,第一趟时9之后就不会再改变了,所以后面我们就无需比较了
因此,我们可以用个下标index来限制
void bubble_sort(int* arr, int sz)
{int i = 0;int index = sz - 1; //这个就是下标位int temporary_index = 0;//趟数for (i = 0; i < sz - 1; i++){int k = 1; //标志位for (int j = 0; j < index; j++){if (arr[j] > arr[j + 1]){int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;k = 0;temporary_index = j;//注意:由于我这里下标是j和j+1,所以这里的temporary_index = j//如果你下标是j和j-1,那么就要不一样了}}if (k == 1){break;}index = temporary_index;}
}
算法复杂度分析
时间复杂度:
普遍的冒泡排序算法的每一轮要遍历所有元素,轮转的次数和元素数量相当,所以时间复杂度是
O(n^2).当然,最优的情况,列已经是顺序的,那么只要进行一次循环遍历一下,所以最优时间复杂度是O(n)
空间复杂度
冒泡排序没有额外开空间,所以空间复杂度为
O(1)
稳定性分析
对于冒泡排序,拿升序举例,只有在前一个数大于后一个数的时候才会交换,小于或者等于都不会改变位置,所以当一前一后两个相同的数出现时,它们最终的相对顺序也不会改变所以冒泡排序是很
稳定的排序
总结
传统的冒泡排序完全可以满足我们最基本的需求,但是也仅仅是最简单的需求,这种简单的两个for循环不加任何的判断语句的形式注定它只能是一种效率较低的算法。虽然能有优化去完善算法,但是总体来说,冒泡排序的效率低.当然冒泡排序也有自身的优点,比如稳定!并且,冒泡排序适合教学,冒泡排序也是许许多多程序员接触的第一个排序算法,所以教学意义重大.
-hive底层原理Mapreduce)
----粘滑运动的动态算法)




-- 获取url路径中的应用名、控制器名、操作名)





——unique_ptr初探)
人机交互设计)
原厂Win10系统)

底层原理剖析+模拟实现)


