1.首次适应算法(First Fit)
1.算法思想:
每次都从低地址开始查找,找到第一个能满足大小的空闲分区。
2.如何实现:
空闲分区以地址递增的次序排列。
每次分配内存时顺序查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
空闲分区表:

空闲分区链:
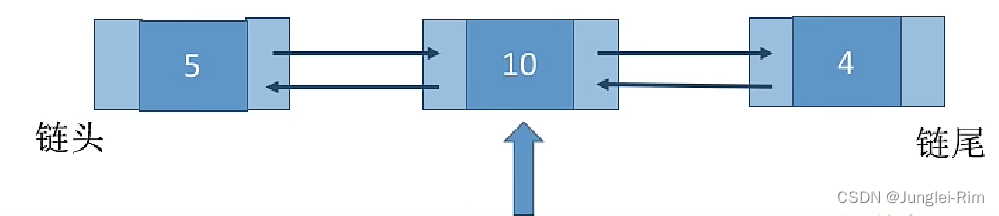
2.最佳适应算法(Best Fit)
1.算法思想:
由于动态分区分配是一种连续分配方式,为各进程分配的空间必须是连续的一整片区域。
因此为了保证当“大进程”到来时能有连续的大片空间,可以尽可能多地留下大片的空闲区,
即,优先使用更小的空闲区。
2.如何实现:
空闲分区按容量递增次序链接。
每次分配内存时顺序查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。

3.缺点:
每次都选最小的分区进行分配,会留下越来越多的、很小的、难以利用的内存块。
因此这种方法会产生很多的外部碎片。
3.最坏适应算法(Worst Fit)
又称最大适应算法(Largest Fit)
1.算法思想:
为了解决最佳适应算法的问题:即留下太多难以利用的小碎片,
可以在每次分配时优先使用最大的连续空闲区,这样分配后剩余的空闲区就不会太小,更方便使用。
2.如何实现:
空闲分区按容量递减次序链接。
每次分配内存时顺序查找空闲分区链(或空闲分区 ),找到大小能满足要求的第一个空闲分区。

3.缺点:
每次都选最大的分区进行分配,虽然可以让分配后留下的空闲区更大,更可用,但是这种方式会导致较大的连续空闲区被迅速用完。
如果之后有“大进程”到达,就没有内存分区可用了。
4.邻近适应算法(Next Fit)
1.算法思想:
首次适应算法每次都从链头开始查找的。
这可能会导致低地址部分出现很多小的空闲分区,而每次分配查找时,都要经过这些分区,因此也增加了查找的开销。
如果每次都从上次找结束的位置开始检索,就能解决上述问题。
2.如何实现:
空闲分区以地址递增的顺序排列(可排成一个循环链表)。
每次分配内存时从上次查找结束的位置开始查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
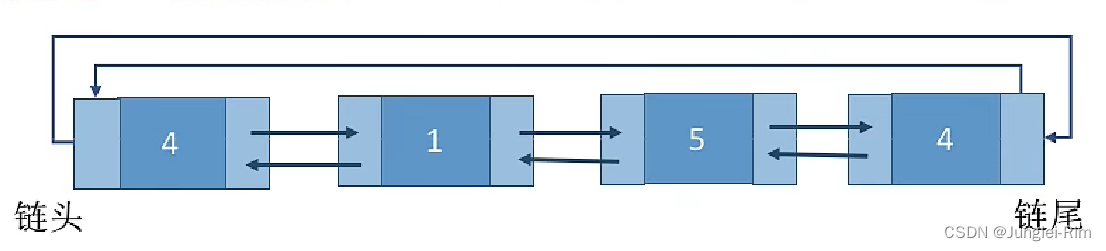
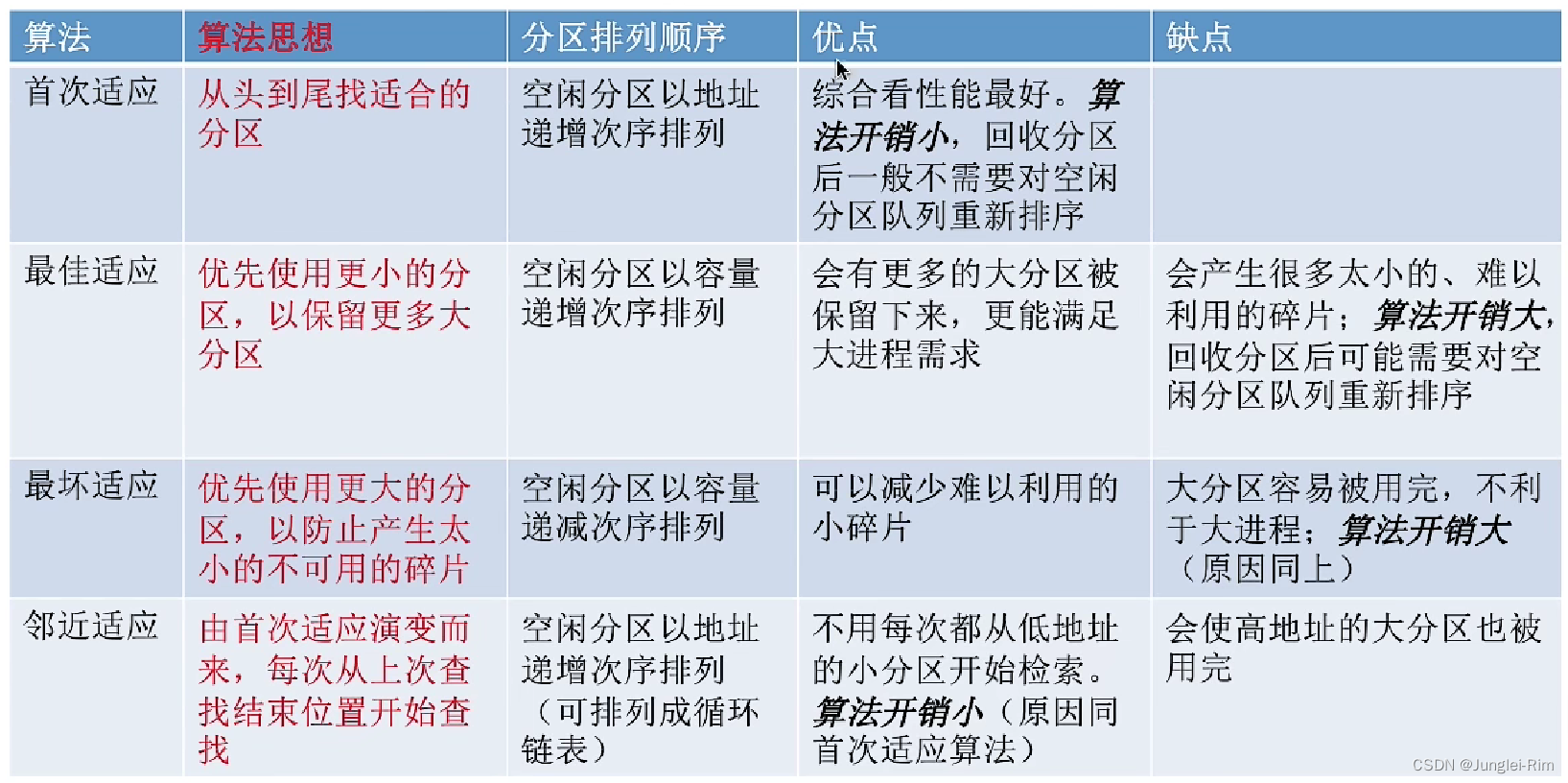
- 首次适应算法每次都要从头查找,每次都需要检索低地址的小分区。但是这种规则也决定了当低地址部分有更小的分区可以满足需求时,会更有可能用到低地址部分的小分区,也会更有可能把高地址部分的大分区保留下来(最佳适应算法的优点)
- 邻近适应算法的规则可能会导致无论低地址、高地址部分的空闲分区都有相同的概率被使用,也就导致了高地址部分的大分区更可能被使用,划分为小分区,最后导致无大分区可用(最大适应算法的缺点)
综合来看,四种算法中,首次适应算法的效果反而更好.
)








)





, 报错型注入)



