一、题目
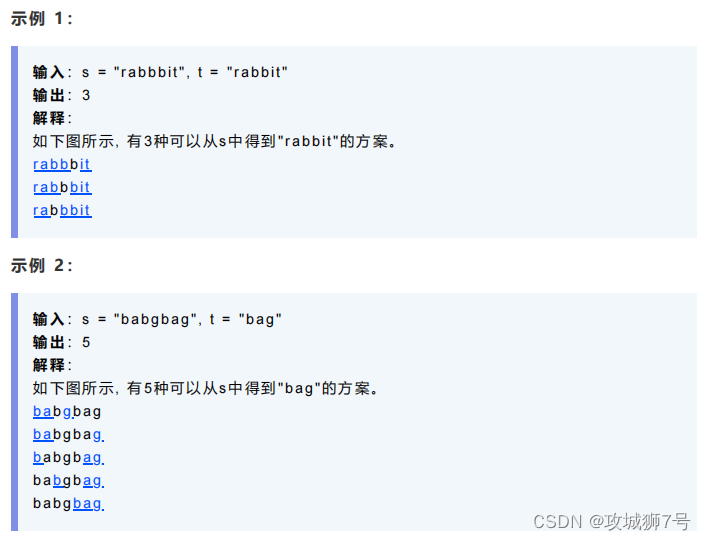
提示：
1）0<=s . length, t. length<=1000
2）s和t由英文字母组成
二、求解思路
动态规划解决思路
s的子序列中出现t的个数，其实就是字符串s的所有子序列中，和字符串t完全一样的有多少个。
我们定义dp[i][ j]表示t的前i个字符可以由s的前j个字符组成的个数（也可以说是字符串s 的前j个字符组成的子序列中，和字符串t 的前i个字符组成的字符串一样的有多少个）。
那么最终我们只需要求出dp[tLength][ sLength]即可（其中tLength和sLength分别表示字符串t和s的长度）。
如果字符串t的第i个字符和字符串s的第j个字符一样，如下所示
如上图所示我们可以有两种选择。
如果字符串t的第i个字符和字符串s的第j个字符不一样，也就是说字符串s的第j个字符不能匹配字符串t的第i个字符。
那么我们只能计算字符串s的前j -1个字符构成的子序列中包含字符串t的前i个字符组成的字符串的个数。
动态规划的三个步骤就是定义状态，列出递推公式，找出边界条件。
详细过程：
我们可以定义二维数组 dp[i][j]，其中 dp[i][j] 表示字符串 t 的前 i 个字符可以由字符串 s 的前 j 个字符组成的子序列的个数。这里，i 的取值范围是 0 到 tLength（包括），j 的取值范围是 0 到 sLength（包括），并且 tLength 和 sLength 分别是字符串 t 和 s 的长度。
初始化时，我们有：
dp[0][j] = 1，对于所有j（包括j = 0），因为空字符串t是s的任何子序列。dp[i][0] = 0，对于所有i > 0，因为s的空子序列不包含任何字符，所以无法与t的任何非空前缀匹配。
接下来，我们考虑 dp[i][j] 的状态转移方程。有两种情况：
- 如果
t[i-1] == s[j-1]（注意字符串索引是从0开始的，所以我们用i-1和j-1来访问实际字符），那么dp[i][j]可以由dp[i-1][j-1]（即t的前i-1个字符与s的前j-1个字符组成的子序列个数）加上dp[i][j-1]（即不选择s[j-1]时，t的前i个字符可以由s的前j-1个字符组成的子序列个数）组成。这是因为我们可以选择将s[j-1]包含在当前子序列中（如果它与t[i-1]匹配），也可以选择不包含它。 - 如果
t[i-1] != s[j-1]，那么dp[i][j]只能由dp[i][j-1]转移而来，因为我们不能选择s[j-1]来匹配t[i-1]。
用数学公式表示状态转移方程，我们有：
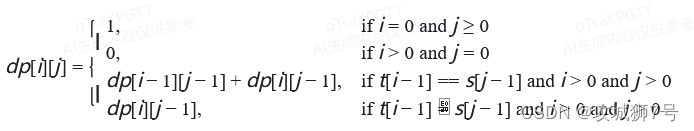
三、代码实现
C代码实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>// 函数 numDistinct 计算字符串 s 中包含字符串 t 作为子序列的不同子序列的数量。
int numDistinct(const char *s, const char *t) {// 获取两个字符串的长度int sLength = strlen(s);int tLength = strlen(t);// 为动态规划表分配内存空间int **dp = (int **)malloc((tLength + 1) * sizeof(int *));for (int i = 0; i <= tLength; i++) {dp[i] = (int *)malloc((sLength + 1) * sizeof(int));memset(dp[i], 0, (sLength + 1) * sizeof(int)); // 初始化为0}// 基础情况初始化，空字符串是任何字符串的子序列，所以初始化为 1for (int j = 0; j <= sLength; j++) {dp[0][j] = 1;}// 填充动态规划表for (int i = 1; i <= tLength; i++) {for (int j = 1; j <= sLength; j++) {// 如果 t 的第 i 个字符和 s 的第 j 个字符相同if (t[i - 1] == s[j - 1]) {// 有两种选择：// 1. 使用 s[j-1] 来匹配 t[i-1] (dp[i-1][j-1])// 2. 不使用 s[j-1] (dp[i][j-1])dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1];} else {// 如果 t 的第 i 个字符和 s 的第 j 个字符不同// 只能选择不使用 s[j-1]dp[i][j] = dp[i][j - 1];}}}// 保存结果int result = dp[tLength][sLength];// 释放动态规划表的内存空间for (int i = 0; i <= tLength; i++) {free(dp[i]);}free(dp);// 返回 t 在 s 中作为子序列出现的总次数return result;
}int main() {const char *s = "rabbbit";const char *t = "rabbit";printf("The number of distinct subsequences is: %d\n", numDistinct(s, t));return 0;
}
在这段代码中：
- 使用
malloc和memset函数分配和初始化动态规划表dp的内存。 - 动态规划表的行
dp[i]表示字符串t的前i个字符在字符串s的前j个字符中作为子序列出现的次数。 - 在计算完成后，使用
free释放动态规划表dp的内存。 main函数提供了一个简单的测试用例来演示函数的使用。
C++代码实现
#include <vector>
#include <string>// 函数 numDistinct 计算字符串 s 中包含字符串 t 作为子序列的不同子序列的数量。
int numDistinct(const std::string& s, const std::string& t) {// 获取两个字符串的长度int sLength = s.length();int tLength = t.length();// 使用 vector 构建二维动态规划表 dp// dp[i][j] 表示 t 的前 i 个字符可以在 s 的前 j 个字符中出现的次数std::vector<std::vector<int>> dp(tLength + 1, std::vector<int>(sLength + 1, 0));// 基础情况初始化，空字符串是任何字符串的子序列，所以初始化为 1for (int j = 0; j <= sLength; j++) {dp[0][j] = 1;}// 填充动态规划表for (int i = 1; i <= tLength; i++) {for (int j = 1; j <= sLength; j++) {// 如果 t 的第 i 个字符和 s 的第 j 个字符相同if (t[i - 1] == s[j - 1]) {// 有两种选择：// 1. 使用 s[j-1] 来匹配 t[i-1] (dp[i-1][j-1])// 2. 不使用 s[j-1] (dp[i][j-1])dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1];} else {// 如果 t 的第 i 个字符和 s 的第 j 个字符不同// 只能选择不使用 s[j-1]dp[i][j] = dp[i][j - 1];}}}// 返回 t 在 s 中作为子序列出现的总次数return dp[tLength][sLength];
}
在这段代码中：
std::vector<std::vector<int>> dp创建了一个二维动态数组来存储中间结果。dp[i][j]表示字符串t的前i个字符在字符串s的前j个字符中作为子序列出现的次数。- 初始化
dp[0][j]为1，因为空字符串是任何字符串的子序列。 - 循环遍历
t和s，根据当前字符是否匹配，更新dp表。 - 最终返回
dp[tLength][sLength]，它包含了t作为s的子序列的出现次数。
