定理1：集合A上的所有一一变换的集合G关于变换的乘法（复合）作成群。

证：首先，恒等变换ɛ:A→A(ɛ(x) = x)是集合A上的一一变换，所以ɛ∈G，即G≠∅；

①对任意的f,g∈G，由映射的性质（见第03篇笔记）可知，一一变换的乘积（复合）还是一一变换，即(f o g),(g o f)∈G，因此满足群公理的第一条：封闭性；

②由变换的性质（见第04篇笔记）知，变换的复合适合结合律，因此也满足群公理的第二条；

③由开头的证明知存在恒等变换ɛ∈G，使得对任意的f∈G和任意的x∈A，有(ɛ o f)(x) = ɛ[f(x)] = f(x)，即ɛ o f = f，因此恒等变换ɛ即是G中的单位元，因此也满足了群公理的第四条；

④对于任意的f∈G，因为f是一一变换，因此f是一个双射，所以f是可逆的，并且f的逆f^(-1)也是一个一一变换，即f^(-1)∈G，且对任意x∈A，(f^(-1) o f)(x) = f^(-1)[f(x)] = x = ɛ(x)，即f^(-1) o f = ɛ，因此任意的f∈G，f在G中都存在逆元，所以也满足了群公理的第五条。

因此由群的第二定义，我们可得集合A上的所有一一变换的集合G关于变换的乘法（复合）作成群，定理得证。

 

例1：设G = {f(x) = x+a|x,a∈R}，G中元素是R上的一一变换，试证：G关于变换的乘法（复合）作成群。

证：①对任意的f(x)=x+a∈G和g(x)=x+b∈G，对任意的x∈R，(f o g)(x) = f[g(x)] = f(x+b) = x+b+a = x+(a+b)，因此(f o g)∈G，所以满足了群公理的第一条：封闭性；

②变换的乘积（复合）适合结合律，因此也满足群公理的第二条；

③存在ɛ(x) = x = x+0∈G，对于任意的f(x) = x+a∈G和任意的x∈R，有(ɛ o f)(x) = ɛ[f(x)] = ɛ(x+a) = x+a = f(x)，因此G中存在单位元ɛ(x)，所以也满足群公理的第四条；

④假设对于任意的f(x)=x+a∈G和任意的x∈R，存在f^(-1)，使得(f^(-1) o f)(x) = f^(-1)[f(x)] = f^(-1)(x+a) = ɛ(x) = x，则f^(-1)=x-a=x+(-a)∈G，因此对于任意的f(x)∈G，f(x)都存在逆元，所以也满足群公理的第五条。

因此由群的第二定义（或者说第二判定定理），我们可知G关于变换的乘法（复合）作成群，命题得证。

 

定理2：令f：R²→R²定义为：

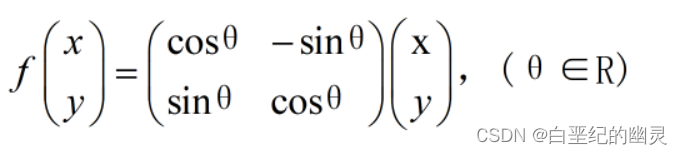
证明：f是R²上的一一变换，也称f为以原点为中心的旋转变换，简称“旋转”。

证：①首先对任意的x,y，都存在唯一的cosθ,sinθ，使得：

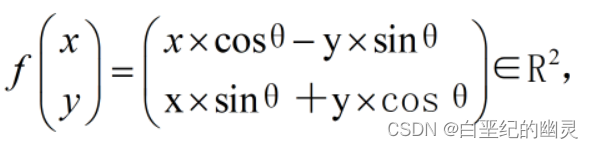
因此f是从R²到R²的变换（或者说“映射”）；

②其次，对任意的(x,y)^T∈R²，存在

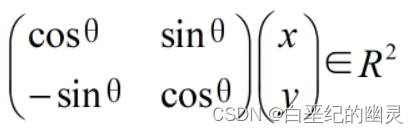
使得：

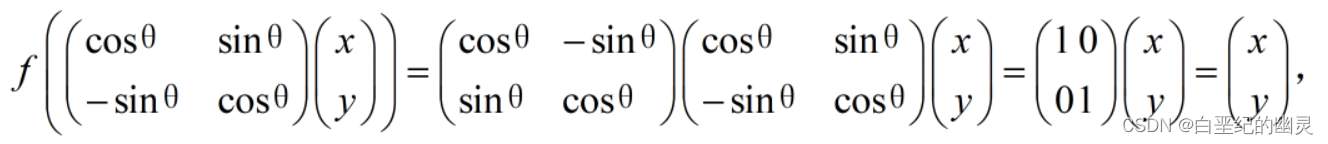
因此f是满射；

③当

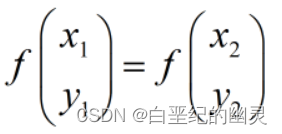
时，有：

两边同时左乘

的逆矩阵

，

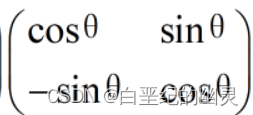可得：

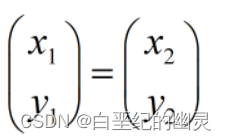
因此f是单射。

综上所述，f是从R²到R²的一一变换（或者说“一一映射”），即f是R²上的一一变换（或者说“一一映射”）。

 

定理3：令f：R²→R²定义为：

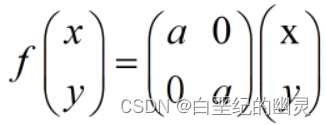
证明f是R²上的一一变换，也称f为以原点为中心的位似变换，简称“位似”（这里a≠0）。

（证明方法和上面定理2的方法类似，也是先证明f是一个映射，再证f是一个满射，最后再证f是一个单射）

 

定理4：令f：R²→R²定义为：

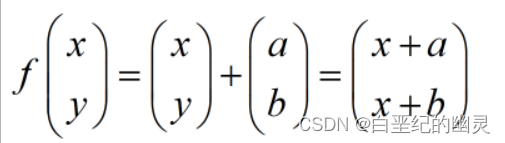
则f也是R²上的一一变换，也称f为平移变换，简称“平移”。

（证明方法同定理2）

 

定理5：令G1,G2,G3分别是所有旋转变换、所有位似变换、所有平移变换组成的集合，o是变换的乘法（复合），则G1,G2,G3都关于o做成群，分别称为“旋转变换群”、“位似变换群”、“平移变换群”。

证明：以证G1为例——

①因为

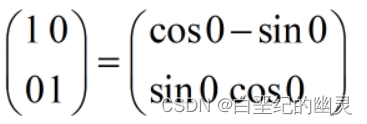
所以恒等变换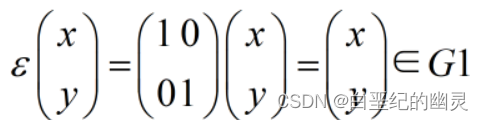

从而G1≠∅；

②对G1中的任意两个元素：

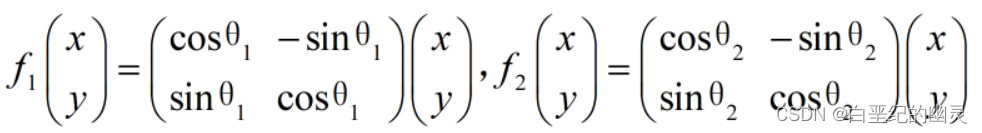
都有：

因此满足群公理的第一条封闭性；

③变换的乘积（复合）适合结合律（见第04篇笔记），因此也满足了群公理的第二条；

④因为

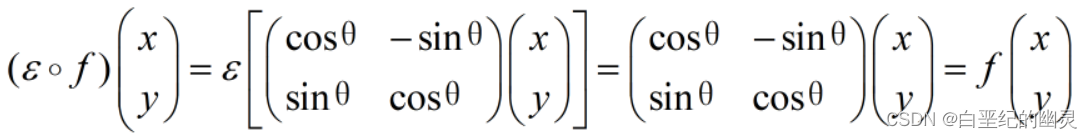
即ɛ o f = f，因此恒等变换ɛ即为群G1中的单位元，所以也满足了群公理的第四条；

⑤令

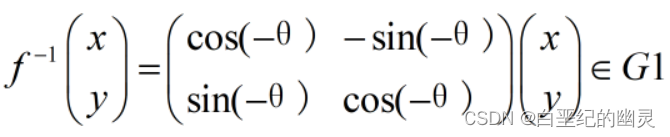
则

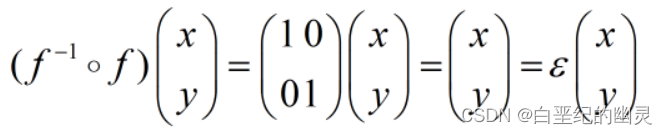
即f^(-1) o f = ɛ，因此对于每一个f∈G1，f在G1中都存在对应的逆元，因此也满足了群公理的第五条。

综上所述，根据群的第二定义（或者说群的第二判定定理），我们可知G1关于o作成群。

G2和G3的情况可用同样的方法去证明。

 

（待续……）