缩放变换
均匀缩放
-
若想将一个图形缩小0.5倍
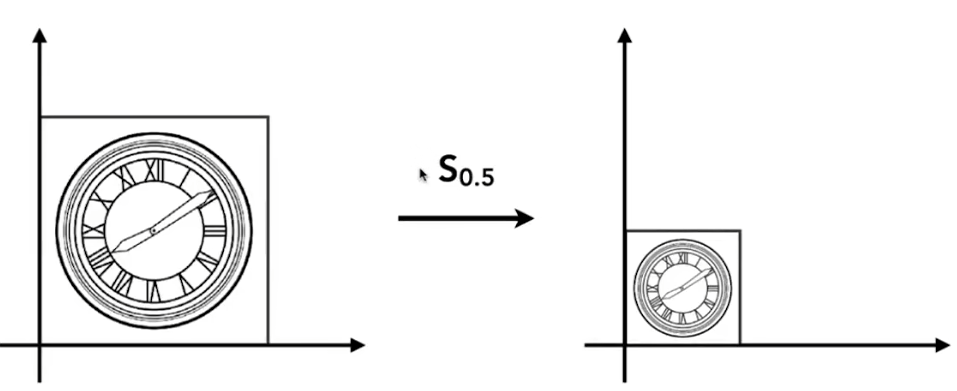
-
若x乘上缩放值s等于x撇,y同理,则 x ′ = s x y ′ = s y \begin{aligned} & x^{\prime}=s x \\ & y^{\prime}=s y \end{aligned} x′=sxy′=sy,这样就表示了x缩小了s倍,y也是
-
将其转为矩阵操作则是在前面乘上一个缩放矩阵 [ x ′ y ′ ] = [ s 0 0 s ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} s & 0 \\ 0 & s \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[s00s][xy],根据矩阵乘法性质,其中的x撇和y撇最后乘出来就是上述的sx和sy。
-
变换矩阵为 [ s 0 0 s ] \left[\begin{array}{ll} s & 0 \\ 0 & s \end{array}\right] [s00s]
非均匀缩放
- x缩放0.5倍,y不变
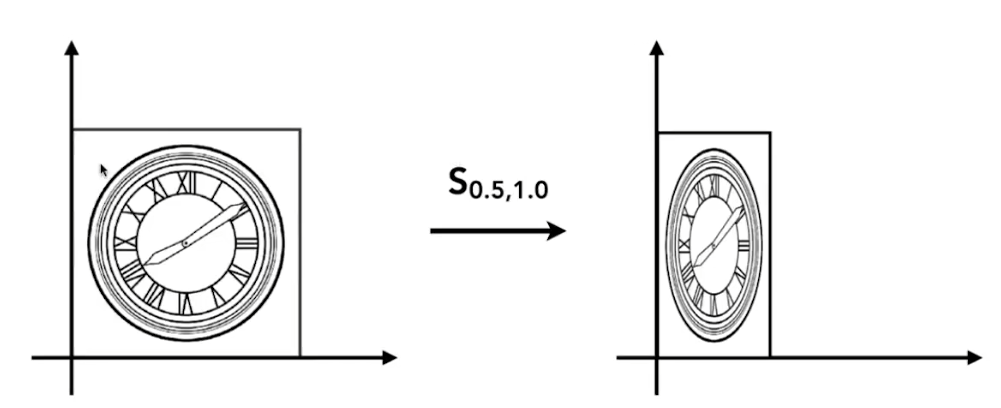
- 和上述公式一样,只不过将对角矩阵的下面那个换一下就行 [ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{cc} s_x & 0 \\ 0 & s_y \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[sx00sy][xy]
- 其中sx为x轴的缩放倍数,sy为y轴。
- 变换矩阵为 [ s x 0 0 s y ] \left[\begin{array}{cc} s_x & 0 \\ 0 & s_y \end{array}\right] [sx00sy]
镜像变换
- 若要将x沿x轴镜像,则表达为 x ′ = − x y ′ = y \begin{aligned} & x^{\prime}=-x \\ & y^{\prime}=y \end{aligned} x′=−xy′=y
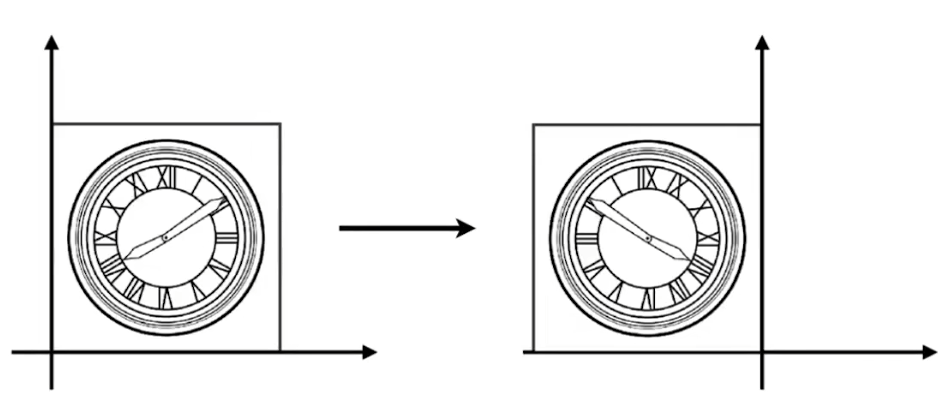
- 其矩阵形式则为 [ x ′ y ′ ] = [ − 1 0 0 1 ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{cc} -1 & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[−1001][xy]
- 变换矩阵为 [ − 1 0 0 1 ] \left[\begin{array}{cc} -1 & 0 \\ 0 & 1 \end{array}\right] [−1001]
剪切变换
- x轴拉长,y轴不变
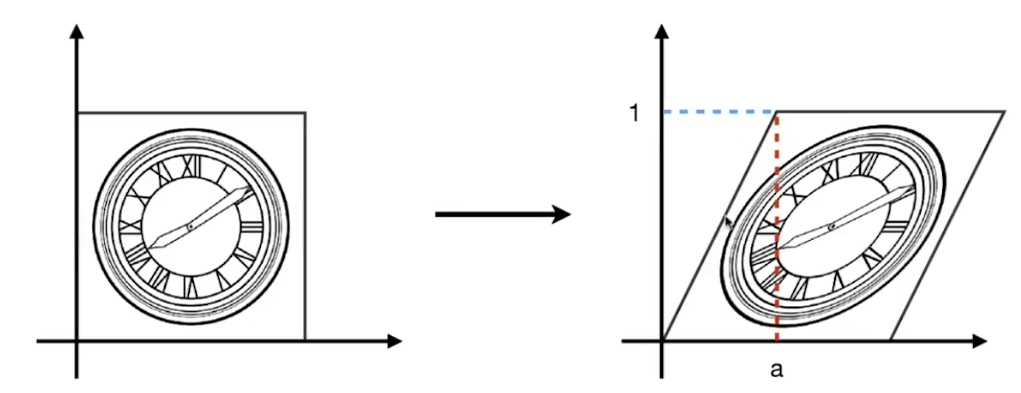
- 当y=0时,水平方向不变
- 当y=1时,水平方向向右移动a个位置
- 于是可推出,当y为1/2时,则移动后的x应该在原本的x+ay处,也就是x根据变换后为x+ay,y不变
- 用矩阵表达则为 [ x ′ y ′ ] = [ 1 a 0 1 ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} 1 & a \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[10a1][xy]
- 变换矩阵为 [ 1 a 0 1 ] \left[\begin{array}{ll} 1 & a \\ 0 & 1 \end{array}\right] [10a1]
旋转变换
- 若无特殊说明,若说A旋转45度,则表示为A绕原点逆时针旋转45度
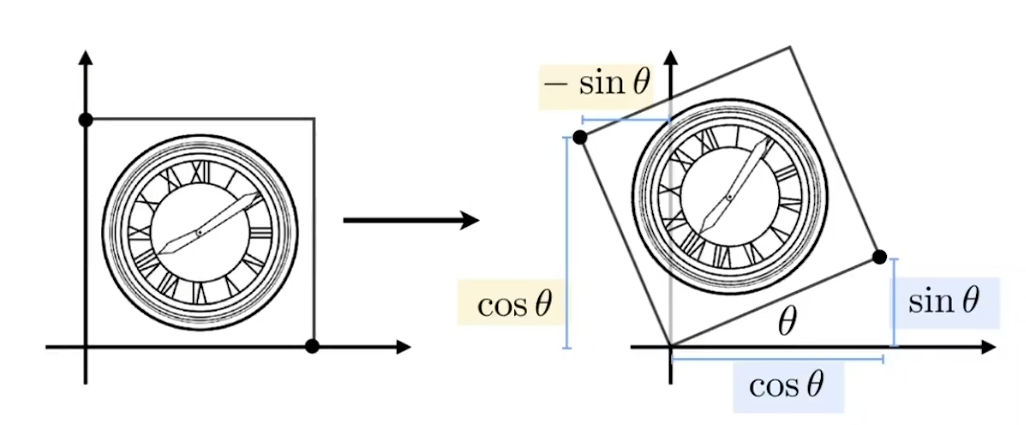
- 则旋转矩阵为 R θ = [ cos θ − sin θ sin θ cos θ ] \mathbf{R}_\theta=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] Rθ=[cosθsinθ−sinθcosθ]
- 也就是 [ x ′ y ′ ] = [ cos θ − sin θ sin θ cos θ ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[cosθsinθ−sinθcosθ][xy]
- 若旋转角度为 − θ -\theta −θ,则旋转矩阵为 R − θ = [ cos θ sin θ − sin θ cos θ ] \mathbf{R}_{-\theta}=\left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right] R−θ=[cosθ−sinθsinθcosθ],其中 cos ( − θ ) = cos ( θ ) , sin ( − θ ) = − sin ( θ ) \cos(-\theta)=\cos(\theta),\sin(-\theta)=-\sin(\theta) cos(−θ)=cos(θ),sin(−θ)=−sin(θ)
- 由此可观察得到, R − θ = R θ T \mathbf{R}_{-\theta}=\mathbf{R}_{\theta}^T R−θ=RθT,我们知道,旋转 θ \theta θ角度和旋转 − θ -\theta −θ角度是互逆的,也就是 R − θ = R θ − 1 \mathbf{R}_{-\theta}=\mathbf{R}_{\theta}^{-1} R−θ=Rθ−1,所以在这可以得到一个很有用的性质,即想求一个图形旋转 − θ -\theta −θ角,我们只需要计算它旋转 θ \theta θ角度矩阵的转置即可。
- 变换矩阵为 [ cos θ − sin θ sin θ cos θ ] \left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] [cosθsinθ−sinθcosθ]
线性变换
- 经过上述变换公式,可以发现其任意一个坐标都可以通过乘上一个系数变成另一个坐标,即 x ′ = a x + b y y ′ = c x + d y \begin{aligned} & x^{\prime}=a x+b y \\ & y^{\prime}=c x+d y \end{aligned} x′=ax+byy′=cx+dy
- 矩阵形式就是 [ x ′ y ′ ] = [ a b c d ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[acbd][xy],也可写成 x ′ = M x \mathbf{x}^{\prime}=\mathbf{M} \mathbf{x} x′=Mx
- 则将这种变换取名为线性变换
平移变换
- x轴移动tx,y轴移动ty

- 则在坐标上的表达为 x ′ = x + t x y ′ = y + t y \begin{aligned} & x^{\prime}=x+t_x \\ & y^{\prime}=y+t_y \end{aligned} x′=x+txy′=y+ty
- 可是这种加法操作,并不能转换为二维矩阵的矩阵变换,也就是乘上一个矩阵从而使得xy移动到x撇y撇
- 只能通过矩阵的加法来实现,也就是 [ x ′ y ′ ] = [ a b c d ] [ x y ] + [ t x t y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]+\left[\begin{array}{l} t_x \\ t_y \end{array}\right] [x′y′]=[acbd][xy]+[txty],而这种形式的变换,被称为仿射变换
- 若不想进行其他变换,也就是旋转啊、缩放啊等,则前面那个abcd矩阵设为单位矩阵
齐次坐标
- 为了使得在进行平移变换的时候或者其他所有的变换都只用乘一个矩阵就完成变换,所以引入了齐次坐标
- 也就是在原有维度的情况下添加了第三个坐标维度w,在原先是2d点的情况变为 ( x , y , 1 ) ⊤ (\mathbf{x}, \mathbf{y}, 1)^{\top} (x,y,1)⊤
- 原先是2d向量的情况现在变为 ( x , y , 0 ) ⊤ (\mathbf{x}, \mathbf{y}, 0)^{\top} (x,y,0)⊤
- 于是我们可以构建出一个矩阵,从而达成只乘一个矩阵就可完成平移变换 ( x ′ y ′ w ′ ) = ( 1 0 t x 0 1 t y 0 0 1 ) ⋅ ( x y 1 ) = ( x + t x y + t y 1 ) \left(\begin{array}{c} x^{\prime} \\ y^{\prime} \\ w^{\prime} \end{array}\right)=\left(\begin{array}{ccc} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \\ 1 \end{array}\right)=\left(\begin{array}{c} x+t_x \\ y+t_y \\ 1 \end{array}\right) x′y′w′ = 100010txty1 ⋅ xy1 = x+txy+ty1
- 只看最右边的前两个值发现就是一个平移操作
- 而为啥二维的点和二维的向量要区分开呢?也就是二维点增加的维度w为1,二维向量增加的维度w为0,主要是因为向量有一个性质,就是一个向量平移到了另一个位置,那它还是那个向量,并不会发生改变
- 而看到上面的公式,若把矩阵右边乘上的向量里的1变为0,则乘完矩阵后的值还是(x, y, 0),这样才符合刚刚说的那个向量平移不变性的性质。
- 同时,区分点和向量还有一个好处就是,向量加向量还是一个向量,例如两个向量相加,比如(x1, y1, 0) + (x2, y2, 0)后为(x1 + x2, y1 + y2, 0),这正好符合向量相加的原则
- 并且当两个点相减的时候,可以理解为是从a点指向到了b点,那么这个a到b就是一个向量,也就是(x1, y1, 1) - (x2, y2, 1) = (x1 - x2, y1 - y2 , 0),这正好也符合两个点相减的意义
- 同理可得一个点加上一个向量,就相当于该点移动了一个向量的位置到了另一个点,也就是(x1, y1, 1) + (x2, y2, 0) = (x1 + x2, y1 + y2, 1),这也正好表现为了一个点
- 所以引入齐次坐标很方便
- 而任何一个仿射变换都可以使用齐次坐标来转换为仅需乘上一个矩阵就可完成变换
- 即 ( x ′ y ′ ) = ( a b c d ) ⋅ ( x y ) + ( t x t y ) \binom{x^{\prime}}{y^{\prime}}=\left(\begin{array}{ll} a & b \\ c & d \end{array}\right) \cdot\binom{x}{y}+\binom{t_x}{t_y} (y′x′)=(acbd)⋅(yx)+(tytx)可转换为 ( x ′ y ′ 1 ) = ( a b t x c d t y 0 0 1 ) ⋅ ( x y 1 ) \left(\begin{array}{l} x^{\prime} \\ y^{\prime} \\ 1 \end{array}\right)=\left(\begin{array}{llc} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \\ 1 \end{array}\right) x′y′1 = ac0bd0txty1 ⋅ xy1
- 也就是现在处理任何一个变换,都可以仅乘一个矩阵就可以完成变换了
- 而引入齐次坐标的上述所有变换矩阵,都可以用以下矩阵表示
- 缩放变换: S ( s x , s y ) = ( s x 0 0 0 s y 0 0 0 1 ) \mathbf{S}\left(s_x, s_y\right)=\left(\begin{array}{ccc} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{array}\right) S(sx,sy)= sx000sy0001
- 旋转变换: R ( α ) = ( cos α − sin α 0 sin α cos 4 α 0 0 0 1 ) \mathbf{R}(\alpha)=\left(\begin{array}{ccc} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos _4 \alpha & 0 \\ 0 & 0 & 1 \end{array}\right) R(α)= cosαsinα0−sinαcos4α0001
- 平移变换: T ( t x , t y ) = ( 1 0 t x 0 1 t y 0 0 1 ) \mathbf{T}\left(t_x, t_y\right)=\left(\begin{array}{ccc} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{array}\right) T(tx,ty)= 100010txty1
- 可发现在二维仿射变换添加齐次坐标后的矩阵最后一行都是(0, 0, 1)。
逆变换
-
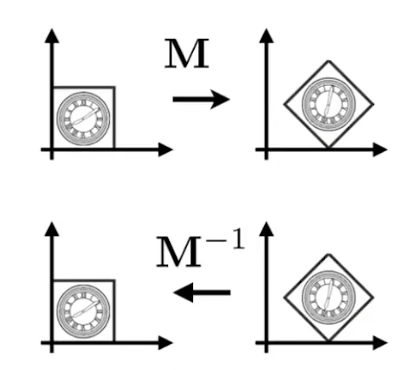
若A点经过一个矩阵M变换成了B点,那么则B点经过一个矩阵 M − 1 M^{-1} M−1可重新变换成A点,这个 M − 1 M^{-1} M−1就是逆变换矩阵
变换矩阵的合并与分解
合并
- 现在假设想将一个图形变换为另一个图形,如下图所示

-
则明显有一个方法,就是利用平移变换和旋转变换
-
但是这里如果先利用平移再旋转,则会出现下图情况
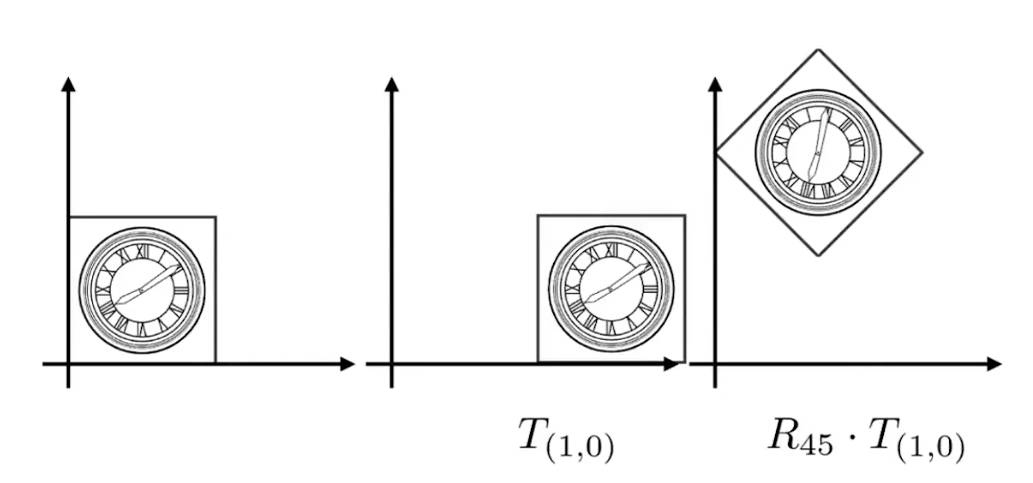
-
可以发现第一个图形并没有变换到我们想要的位置上
-
而如果我们先旋转,再平移,则可以发现可以完美变换到我们想要的位置
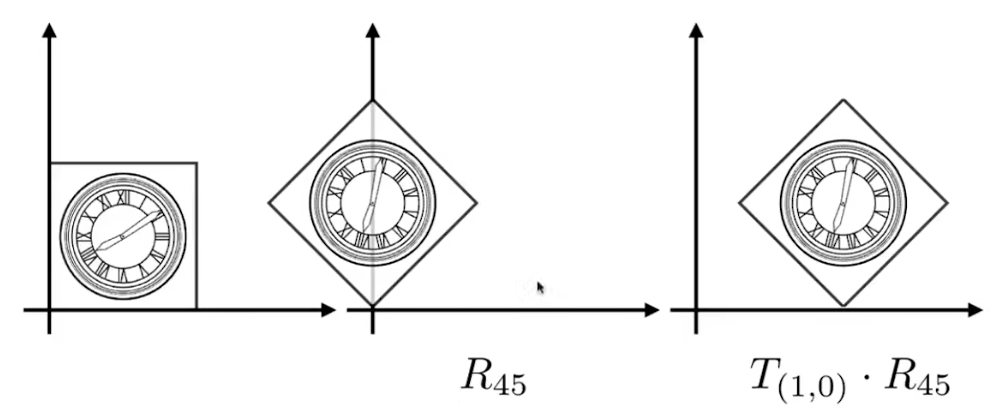
-
这说明变换的顺序是非常重要的,也就是 R 45 ⋅ T ( 1 , 0 ) ≠ T ( 1 , 0 ) ⋅ R 45 R_{45} \cdot T_{(1,0)} \neq T_{(1,0)} \cdot R_{45} R45⋅T(1,0)=T(1,0)⋅R45
-
也就是我们要先将向量和旋转矩阵相乘,再进行平移变换,即 T ( 1 , 0 ) ⋅ R 45 [ x y 1 ] = [ 1 0 1 0 1 0 0 0 1 ] [ cos 4 5 ∘ − sin 4 5 ∘ 0 sin 4 5 ∘ cos 4 5 ∘ 0 0 0 1 ] [ x y 1 ] T_{(1,0)} \cdot R_{45}\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{lll} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} \cos 45^{\circ} & -\sin 45^{\circ} & 0 \\ \sin 45^{\circ} & \cos 45^{\circ} & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right] T(1,0)⋅R45 xy1 = 100010101 cos45∘sin45∘0−sin45∘cos45∘0001 xy1
-
然后我们计算顺序则是要从右到左进行运算
-
而又由于矩阵有结合律,也就是(A*B)*C = A*(B*C),那么我们可以先将前面几个变换矩阵先乘为一个矩阵,再用该矩阵去乘上向量,从而使得这个矩阵可以表示前面所有的变换操作,即 A n ( … A 2 ( A 1 ( x ) ) ) = A n ⋯ A 2 ⋅ A 1 ⋅ ( x y 1 ) A_n\left(\ldots A_2\left(A_1(\mathbf{x})\right)\right)=\mathbf{A}_n \cdots \mathbf{A}_2 \cdot \mathbf{A}_1 \cdot\left(\begin{array}{l} x \\ y \\ 1 \end{array}\right) An(…A2(A1(x)))=An⋯A2⋅A1⋅ xy1
-
因为这些变换矩阵都是3*3的,所以当他们乘完之后的最后的矩阵也肯定还是3*3的,也就是说最后乘完的这个矩阵可以表示出非常复杂的变换
分解
-
一般情况下我们说旋转默认都是按照原点逆时针开始旋转,但是假设我现在想要按照当前图形的左下角进行旋转,应该怎么办呢。
-
例如要将如下图像的最左侧图形变换到最右侧
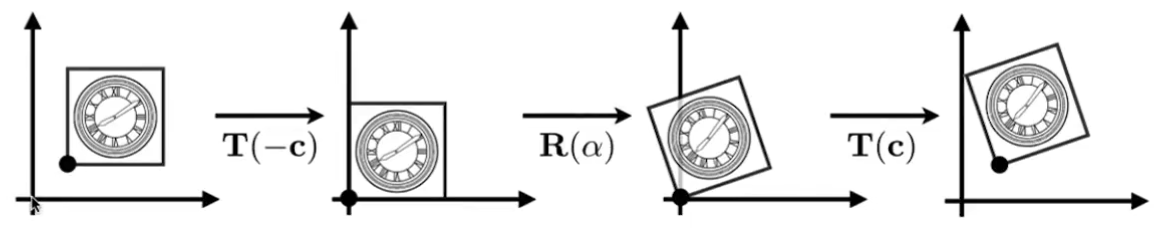
-
如果直接就旋转变换,由于旋转是默认对着原点旋转的,所以就很难变成最右边的图形,那么我们就可以将步骤分解,先把图形移动到原点,然后再旋转变换,再移动回原位即可。
-
矩阵形式表达即 T ( c ) ⋅ R ( α ) ⋅ T ( − c ) \mathbf{T}(\mathbf{c}) \cdot \mathbf{R}(\alpha) \cdot \mathbf{T}(-\mathbf{c}) T(c)⋅R(α)⋅T(−c)







-- 高性能可配置Echarts图表组件封装)





关于基础资料/单据实体的id)

、重定义(同名隐藏)的区别 (超详解))

)

![和Bug较劲的第n天:[Error: Unable to open snapshot file: No such file or directory]](http://pic.xiahunao.cn/和Bug较劲的第n天:[Error: Unable to open snapshot file: No such file or directory])