微分方程与动力系统

1. 微分方程的理论基础

微分方程在物理、工程、生物学等诸多领域有着广泛应用，它们用于描述许多自然现象和工程问题。掌握微分方程的基础理论对理解和解决实际问题至关重要。

1.1 函数、导数与微分

函数是数学中描述变量之间关系的基本概念。设 $y=f(x)$ 是一个函数，表示变量 $y$ 随变量 $x$ 的变化关系。导数是函数变化率的度量，定义为：
$$f^{\prime }(x)=\underset{\Delta x\to 0}{\lim }\frac{f(x+\Delta x)-f(x)}{\Delta x}$$

微分是导数在微小变化下的线性近似。对于函数 $y=f(x)$，它的微分表示为：
$$dy=f^{\prime }(x)dx$$

示例：
考虑函数 $y=x^2$，则其导数为 $f^{\prime }(x)=2x$，对应的微分为：
$$dy=2xdx$$

1.2 一阶线性微分方程的解

一阶线性微分方程的一般形式为：
$$\frac{dy}{dx}+P(x)y=Q(x)$$

它的解法包括求解齐次方程和非齐次方程。齐次方程的形式为：
$$\frac{dy}{dx}+P(x)y=0$$

其通解为：
$$y=C{e}^{-\int P(x)dx}$$
其中， $C$ 是任意常数。

对于非齐次方程，可以通过引入积分因子 $\mu (x)=e^{\int P(x)dx}$ 转化为：
$$\mu (x)\frac{dy}{dx}+\mu (x)P(x)y=\mu (x)Q(x)$$
$$\frac{d}{dx}[\mu (x)y]=\mu (x)Q(x)$$

积分得到通解：
$$y=\frac{1}{\mu (x)}\left(\int \mu (x)Q(x)dx+C\right)$$

示例：
解方程 $\frac{dy}{dx}+2y=e^x$

1. 求积分因子 $\mu (x)=e^{\int 2dx}=e^{2x}$
2. 变换方程： $e^{2x}\frac{dy}{dx}+2e^{2x}y=e^x{e}^{2x}$
3. 简化为： $\frac{d}{dx}[e^{2x}y]=e^{3x}$
4. 积分得到： $e^{2x}y=\int e^{3x}dx=\frac{e^{3x}}{3}+C$
5. 最终解为： $y=\frac{e^x}{3}+C{e}^{-2x}$

1.3 二阶常系数线性微分方程的解

二阶常系数线性微分方程的一般形式为：
$$a\frac{d^{2}y}{d{x}^2}+b\frac{dy}{dx}+cy=0$$

其特征方程为：
$$a{r}^2+br+c=0$$

根据特征方程的根，方程的解有三种情况：

1. 两个实根 $r_1$ 和 $r_2$：
   $$y=C_1{e}^{r_{1}x}+C_2{e}^{r_{2}x}$$

2. 一个实根 $r$：
   $$y=(C_1+C_{2}x)e^{rx}$$

3. 一对共轭复根 $r=\alpha \pm \beta i$：
   $$y=e^{\alpha x}(C_1\cos (\beta x)+C_2\sin (\beta x))$$

示例：
解方程 $y^{\prime \prime }-3y^{\prime }+2y=0$

1. 写出特征方程： $r^2-3r+2=0$
2. 求根： $r_1=1$, $r_2=2$
3. 通解为： $y=C_1{e}^x+C_2{e}^{2x}$

---

通过对函数、导数与微分的理解，以及一阶和二阶常系数线性微分方程的解法，我们可以解决许多实际问题。在实际应用中，通常会涉及到初值条件和边值条件的微分方程，需要根据具体问题进一步求解。

2. 使用python求解微分方程

在Python中，我们可以使用Numpy和SciPy这两个库来进行函数的微分和积分计算。

2.1 求解微分

在此举例：求解函数f(x) = x^2在点x = 1处的导数：

import numpy as np
# 定义x的取值范围和步长
x = np.linspace(0, 2, 100)
y = x**2
# 计算导数
dydx = np.gradient(y, x)
# 在x=1处的导数值
derivative_at_1 = dydx[np.argmin(abs(x - 1))]
print(f'在x=1处的导数值是：{derivative_at_1}')

np.gradient 函数计算数组 y 的梯度，返回 y 对 x 的导数。这个函数采用有限差分方法来近似计算导数。

np.argmin(abs(x - 1)) 计算 x 数组中与 1 最接近的值的索引。通过这个索引，我们可以找到对应的导数值 dydx。

2.2 求解定积分

在此举例：计算函数f(x) = cos(2πx) * exp(-x) + 1.2在区间[0, 0.7]上的定积分。

import numpy as np
from scipy.integrate import quad
# 定义函数
def f(x):return np.cos(2 * np.pi * x) * np.exp(-x) + 1.2

2.2.1 quad函数求解

使用SciPy库中的quad函数求解定积分：

def test():# 计算定积分integral, error = quad(f, 0, 0.7)print(f'定积分的结果是：{integral}')

2.2.2 梯型法则求解

使用数值积分的方法来近似计算，在此以梯型法则为例编写程序：

def tixing():# h = x[1]-x[0];# 积分区间x0 = 0xn = 0.7# 步长n = 1000  # 分成1000个小区间h = (xn - x0) / ns = 0for i in range(n):xn = x0 + i * hxn1 = xn + h;yn = f(xn)yn1 = f(xn1)s0 = (yn + yn1) * h / 2s += s0print(s)

3. 使用Scipy和Sympy解微分方程

3.1 使用sympy求解微分方程解析解

背景：大多数微分方程是求不出解析解的，只能在不同取值条件下求一个数值解。

3.2 求解微分方程的方法

在解决微分方程时，我们可以使用解析方法或数值方法。解析方法能给出精确的解，数值方法则在解析解难以获得时提供近似解。下面我们将分别使用 SymPy 和 SciPy 来求解微分方程。

3.2.1 使用 SymPy 求解微分方程解析解

SymPy 是一个用于符号计算的 Python 库，能够求解各种类型的微分方程。

示例：求解一阶线性微分方程

考虑一阶线性微分方程：
$$\frac{dy}{dx}+y=e^x$$

使用 SymPy 求解：

import sympy as sp# 定义符号变量
x = sp.symbols('x')
y = sp.Function('y')(x)# 定义微分方程
ode = sp.Eq(y.diff(x) + y, sp.exp(x))# 求解微分方程
solution = sp.dsolve(ode, y)
print(solution)

解释：

1. 导入 SymPy 库。
2. 定义符号变量 x 和函数 y(x)。
3. 定义微分方程 (\frac{dy}{dx} + y = e^x)。
4. 使用 dsolve 函数求解微分方程，得到解析解。

示例：求解二阶常系数线性微分方程

考虑二阶常系数线性微分方程：
$$y^{\prime \prime }-3y^{\prime }+2y=0$$

使用 SymPy 求解：

import sympy as sp# 定义符号变量
x = sp.symbols('x')
y = sp.Function('y')(x)# 定义微分方程
ode = sp.Eq(y.diff(x, x) - 3*y.diff(x) + 2*y, 0)# 求解微分方程
solution = sp.dsolve(ode, y)
print(solution)

解释：

1. 导入 SymPy 库。
2. 定义符号变量 x 和函数 y(x)。
3. 定义二阶微分方程 $y^{\prime \prime }-3y^{\prime }+2y=0$。
4. 使用 dsolve 函数求解微分方程，得到解析解。

2.2.2 使用 SciPy 求解微分方程数值解

SciPy 是一个用于科学和技术计算的 Python 库，它包含许多用于数值求解微分方程的工具。Python求解微分方程数值解可以使用scipy库中的integrate包。在这当中有两个重要的函数：odeint和solve_ivp。但本质上，从底层来讲求解微分方程数值解的核心原理都是Euler 法和Runge-Kutta 法。

2.2.2.1使用 odeint 求解一阶微分方程

odeint()函数需要至少三个变量，第一个是微分方程函数，第二个是微分方程初值，第三个是微分的自变量。

示例：使用 odeint 求解一阶微分方程

考虑一阶微分方程：
$$\frac{dy}{dx}=-2y+1$$
初始条件 $y(0)=0$

使用 SciPy 求解：

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt# 定义函数
def model(y, x):dydx = -2*y + 1return dydx# 初始条件
y0 = 0# x 的取值范围
x = np.linspace(0, 5, 100)# 求解微分方程
y = odeint(model, y0, x)# 绘制结果
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Solution of dy/dx = -2y + 1')
plt.show()

解释：

1. 导入必要的库：numpy, odeint 和 matplotlib。
2. 定义微分方程的函数 model，返回导数 dydx。
3. 设置初始条件 y0 = 0。
4. 定义 x 的取值范围。
5. 使用 odeint 函数求解微分方程。
6. 使用 matplotlib 绘制解的曲线。

2.2.2.2使用 odeint 求解高阶微分方程

使用 odeint 求解高阶微分方程
Python求解微分方程数值解的时候是无法直接求解高阶微分方程的，必须通过换元降次的方法实现低阶化，把一个高阶微分方程替换成若干个一阶微分方程组成的微分方程组才能求解。

odeint 函数可以用于求解高阶微分方程。为了使用 odeint 求解高阶微分方程，我们需要将其转换为一组一阶微分方程。这里是一个示例，展示如何使用 odeint 求解二阶微分方程：

考虑以下二阶微分方程：
$$y^{\prime \prime }-3y^{\prime }+2y=0$$
初始条件为 $y(0)=1$ 和 $y^{\prime }(0)=0$。

步骤：

1. 将二阶方程转换为一阶方程组：
   设 $y_1=y$， $y_2=y^{\prime }$。则原方程可以转换为以下系统：
   $$\{\begin{array}{l}{y}_1^{\prime }=y_2\\ y_2^{\prime }=3y_2-2y_1\end{array}$$

2. 定义初始条件：
   $y_1(0)=1$， $y_2(0)=0$。

3. 使用 odeint 进行求解。

下面是具体的代码示例：

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt# 定义微分方程组
def model(y, t):y1, y2 = ydy1dt = y2dy2dt = 3*y2 - 2*y1return [dy1dt, dy2dt]# 初始条件
y0 = [1, 0]# 时间点
t = np.linspace(0, 5, 100)# 求解微分方程组
solution = odeint(model, y0, t)# 提取解
y1 = solution[:, 0]
y2 = solution[:, 1]# 绘制结果
plt.plot(t, y1, label='y(t)')
plt.plot(t, y2, label="y'(t)")
plt.xlabel('t')
plt.ylabel('y')
plt.legend()
plt.title("Solution of the differential equation y'' - 3y' + 2y = 0")
plt.show()

代码解释：

1. 导入库：导入 numpy，odeint 和 matplotlib 库。
2. 定义微分方程组：将二阶微分方程转化为两个一阶微分方程，并定义为函数 model。
3. 初始条件：设置初始条件 $y_1(0)=1$， $y_2(0)=0$。
4. 时间点：定义时间范围 [0, 5]，并生成 100 个等间距点。
5. 求解微分方程组：使用 odeint 函数求解，并返回解数组。
6. 提取解：从解数组中提取 $y_1(t)$ 和 $y_2(t)$。
7. 绘制结果：使用 matplotlib 绘制 $y_1(t)$ 和 $y_2(t)$ 随时间变化的曲线。

通过这些步骤，我们成功地使用 odeint 求解了一个高阶微分方程，并将结果进行了可视化。这个方法可以扩展到更高阶的微分方程，只需将其转换为对应的一阶微分方程组即可。

2.2.2.3 使用 solve_ivp 求解一阶微分方程

Solve_ivp函数的用法与odeint非常类似，只不过比odeint多了两个参数。一个是t_span参数，表示自变量的取值范围；另一个是method参数，可以选择多种不同的数值求解算法。常见的内置方法包括RK45, RK23, DOP853, Radau, BDF等多种方法，通常使用RK45多一些。
示例：使用 solve_ivp 求解一阶微分方程

考虑相同的一阶微分方程：
$$\frac{dy}{dx}=-2y+1$$
初始条件 $y(0)=0$

使用 solve_ivp 求解：

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt# 定义函数
def model(x, y):dydx = -2*y + 1return dydx# 初始条件
y0 = [0]# x 的取值范围
x_span = (0, 5)
x = np.linspace(0, 5, 100)# 求解微分方程
sol = solve_ivp(model, x_span, y0, t_eval=x)# 绘制结果
plt.plot(sol.t, sol.y[0])
plt.xlabel('x')
plt.ylabel('y')
plt.title('Solution of dy/dx = -2y + 1')
plt.show()

解释：

1. 导入必要的库：numpy, solve_ivp 和 matplotlib。
2. 定义微分方程的函数 model，返回导数 dydx。
3. 设置初始条件 y0 = [0]。
4. 定义 x 的取值范围 x_span 和用于评估的点 x。
5. 使用 solve_ivp 函数求解微分方程。
6. 使用 matplotlib 绘制解的曲线。

由于没有设置method参数，这里默认solve_ivp使用RK45（4-5阶 Runge-Kutta 法）方法进行求解。

以上示例展示了如何使用 SymPy 求解微分方程的解析解，以及如何使用 SciPy 求解微分方程的数值解。通过这些方法，我们可以处理各种类型的微分方程，满足不同应用场景的需求。

2.2.2.4 odeint和solve_ivp方法对比

上面学习了如何调用odeint和solve_ivp解微分方程，接下来对两种方法进行对比总结：

• odeint分析

odeint 是 SciPy 库中经典的 ODE 求解器，基于 LSODA 算法，能够自动在非刚性和刚性方法之间切换。以下是一些特点：

优点：

1. 简单易用：适合快速求解常见的 ODE 问题。
2. 自动方法选择：根据问题的性质自动选择合适的算法（非刚性或刚性）。
3. 广泛使用：在很多早期的应用和文献中使用广泛，社区支持强大。

缺点：

1. 有限的功能：无法处理事件（events）或不连续点，不支持更多高级功能。
2. 未来维护不确定：虽然目前仍在使用，但未来可能逐渐被 solve_ivp 所取代。

• solve_ivp分析

solve_ivp 是 SciPy 库中较新的 ODE 求解器，提供了更多的灵活性和功能，支持多种算法。以下是一些特点：

优点：

1. 多种算法选择：支持多种求解算法（如 RK45, RK23, BDF, LSODA 等），用户可以根据问题选择最合适的算法。
2. 事件处理：支持事件（events）功能，可以处理不连续点和终止条件等高级功能。
3. 灵活性高：提供更多配置选项，适合复杂问题的求解。

缺点：

1. 稍微复杂：相对于 odeint，使用稍微复杂一些，特别是涉及到高级功能时。
2. 较新：虽然功能更强大，但一些传统用户可能更习惯于使用 odeint。

• 对比总结

特点	odeint	solve_ivp
易用性	较简单	相对复杂
算法选择	自动选择非刚性或刚性算法	用户可选择多种算法
高级功能	不支持事件处理	支持事件处理、更多配置选项
维护和未来前景	经典方法，可能逐渐被 solve_ivp 取代	较新方法，未来维护和发展前景更好
社区支持	使用广泛，社区支持强大	支持不断增加，功能更强大

2.3 偏微分方程的数值求解

有限差分法是一种数值方法，通过使用离散点上的差分来逼近微分，进而求解偏微分方程。

以下是使用有限差分法求解偏微分方程的一般步骤：

2.3.1 离散化区域

将求解区域离散化，即将连续的空间和时间划分为有限个离散点。例如，在二维空间上，网格点可以表示为 $(x_i,y_j)$，时间点可以表示为 $t_k$。

示例：
对于一个在二维空间和时间上的偏微分方程，我们可以将区域划分为一个 $m\times n$ 的网格：

$$x_i=x_{\text{min}}+i\Delta x,y_j=y_{\text{min}}+j\Delta y,t_k=t_{\text{min}}+k\Delta t$$

其中，$\Delta x$、$\Delta y$ 和 $\Delta t$ 分别是空间和时间步长，(i, j, k) 是整数索引。

2.3.2. 差分公式

将偏微分方程中的微分项用差分公式代替。常见的差分公式包括前向差分、后向差分和中心差分。

示例：
对于一维热传导方程：

$$\frac{\partial u}{\partial t}=\alpha \frac{{\partial }^{2}u}{\partial x^2}$$

可以使用前向差分来逼近时间导数，中心差分来逼近空间导数：

$$\frac{u_i^{k+1}-u_i^k}{\Delta t}=\alpha \frac{u_{i+1}^k-2u_i^k+u_{i-1}^k}{(\Delta x{)}^2}$$

2.3.3 边界条件和初始条件

在离散化网格上设置边界条件和初始条件。

示例：
对于热传导方程，边界条件可以是定值边界条件（Dirichlet）或绝热边界条件（Neumann）。初始条件是 $t=0$ 时刻的温度分布：

$$u_i^0=f(x_i)$$

2.3.4 构造代数方程组

根据差分公式，将偏微分方程转化为代数方程组。在每个离散点上，写出相应的代数方程。

2.3.5 求解代数方程组

使用数值方法（如高斯消元法、LU分解法或迭代法）求解代数方程组，得到离散点上的解。

2.3.6 后处理

对得到的离散点上的数值解进行后处理，如插值、绘图、误差分析等。

示例代码：一维热传导方程

以下是使用有限差分法求解一维热传导方程的Python代码示例：

import numpy as np
import matplotlib.pyplot as plt# 参数设置
L = 1.0      # 杆的长度
T = 0.1      # 总时间
alpha = 0.01 # 热传导系数
Nx = 50      # 空间离散点数
Nt = 1000    # 时间离散点数dx = L / (Nx - 1)
dt = T / Nt
x = np.linspace(0, L, Nx)
t = np.linspace(0, T, Nt)# 初始条件 u(x,0) = sin(pi*x)
u = np.sin(np.pi * x)# 时间步进
for k in range(Nt):u_new = u.copy()for i in range(1, Nx - 1):u_new[i] = u[i] + alpha * dt / dx**2 * (u[i+1] - 2*u[i] + u[i-1])u = u_new# 绘图
plt.plot(x, u, label='Numerical Solution')
plt.xlabel('x')
plt.ylabel('u')
plt.title('1D Heat Conduction')
plt.legend()
plt.show()

4.微分方程案例

5. 差分方程案例

6. 元胞自动机

6.1 元胞自动机介绍

元胞自动机（Cellular Automaton，CA）是一种离散的数学模型，由具有有限状态的元胞和规则组成，用于模拟复杂系统中的局部互动和全局演化。元胞自动机的基本结构包括：

1. 网格：通常是二维的矩形网格，但也可以是其他形状。
2. 元胞：每个网格点代表一个元胞，具有有限的状态集。
3. 邻居：每个元胞有一个邻居集，定义了元胞之间的互动范围。常见的邻居类型包括Moore邻居（八个方向）和Von Neumann邻居（四个方向）。
4. 规则：元胞状态根据特定的局部规则进行更新，规则通常依赖于元胞当前状态及其邻居的状态。

一个经典的元胞自动机示例是康威的“生命游戏”（Conway’s Game of Life），其中元胞的状态是生或死，通过简单的规则模拟生物群体的演化。

6.2 元胞自动机的应用场景

元胞自动机因其简单的结构和强大的模拟能力，在多个领域得到了广泛应用：

1. 生物学：用于模拟细胞的生长和分裂、生物群体的演化等。
2. 物理学：模拟晶体生长、流体动力学、扩散过程等。
3. 计算科学：用于研究计算过程、开发新型计算模型，如量子计算。
4. 社会科学：模拟城市发展、交通流量、疫情传播等社会现象。
5. 生态学：用于模拟生态系统的动态变化和物种之间的互动。
6. 图像处理：应用于图像分割、边缘检测等领域。

6.3 元胞自动机的优点

元胞自动机具有以下优点：

1. 简单性：模型结构简单，规则易于理解和实现。
2. 并行性：元胞自动机的计算可以天然地并行化，适合高性能计算和分布式计算。
3. 局部性：规则基于局部信息，不需要全局知识，适用于大规模系统的模拟。
4. 灵活性：可以通过改变规则和邻居结构来适应不同的应用场景。
5. 自组织行为：能够模拟复杂系统中的自组织现象，如模式形成、集群行为等。

示例：康威的“生命游戏”

“生命游戏”是最著名的元胞自动机之一，用于展示元胞自动机的基本原理和应用，生命游戏（Game of Life）是由英国数学家约翰·康威（John Horton Conway）于1970年发明的一种元胞自动机。它是一个零玩家游戏，意味着游戏的演化是由初始状态决定的，不需要玩家的进一步输入。生命游戏的规则非常简单，但它能够产生极其复杂的行为，被誉为“元胞自动机的代表作”。生命游戏的规则如下：

• （Exposure）当前细胞为存活状态时，当周围的存活细胞低于2个时（不包含2个），该细胞变成死亡状态
• （Survive）当前细胞为存活状态时，当周围有2个或3个存活细胞时，该细胞保持原样
• （Overcrowding）当前细胞为存活状态时，当周围有超过3个存活细胞时，该细胞变成死亡状态
• （Reproduction）当前细胞为死亡状态时，当周围有3个存活细胞时，该细胞变成存活状态

Python 实现：

import numpy as np
import matplotlib.pyplot as pltdef initialize_grid(size):"""初始化网格，随机填充0和1"""return np.random.choice([0, 1], size*size).reshape(size, size)def count_neighbors(grid, x, y):"""计算元胞(x, y)的活邻居数"""return np.sum(grid[max(0, x-1):min(grid.shape[0], x+2), max(0, y-1):min(grid.shape[1], y+2)]) - grid[x, y]def update_grid(grid):"""根据生命游戏规则更新网格"""new_grid = grid.copy()for i in range(grid.shape[0]):for j in range(grid.shape[1]):alive_neighbors = count_neighbors(grid, i, j)if grid[i, j] == 1:# Exposure: 少于2个邻居，细胞死亡if alive_neighbors < 2:new_grid[i, j] = 0# Survive: 2或3个邻居，细胞保持存活elif alive_neighbors in [2, 3]:new_grid[i, j] = 1# Overcrowding: 超过3个邻居，细胞死亡else:new_grid[i, j] = 0else:# Reproduction: 恰好3个邻居，细胞复活if alive_neighbors == 3:new_grid[i, j] = 1return new_grid# 设置网格大小和步数
size = 50
steps = 100# 初始化网格
grid = initialize_grid(size)# 动画展示
fig, ax = plt.subplots()
img = ax.imshow(grid, interpolation='nearest', cmap='binary')def animate(frame):global gridgrid = update_grid(grid)img.set_data(grid)return img,ani = plt.FuncAnimation(fig, animate, frames=steps, interval=100, blit=True)
plt.show()

7. 数值计算方法与微分方程求解

在Python中，数值计算方法主要依赖于一些专门的库，如NumPy、SciPy和SymPy等。这些库提供了丰富的数学函数和算法，用于处理线性代数、微积分、优化问题等。例如，SciPy中的scipy.optimize模块可以用于求解函数的极值，scipy.integrate模块可以用于数值积分，而scipy.linalg模块则提供了线性代数的相关功能。通过这些工具，我们可以在Python中有效地进行数值计算和求解微分方程。
程序库函数求解极大缩短我们的计算耗时，使得模型求解不再头疼，但我们不应只成为调包侠，还应了解程序的底层数值计算方法，下面是我们日常建模中常用到的微分方程求解方法。

7.1 梯度下降法

梯度下降法是一种用于寻找函数最小值的优化算法，尤其在机器学习中广泛应用。它的基本思想是沿着函数梯度的反方向迭代，逐步逼近最小值。

基本步骤：

1. 初始化参数 $\theta$。
2. 计算目标函数 $J(\theta )$ 对参数的梯度 $\nabla J(\theta )$。
3. 更新参数：$\theta =\theta -\alpha \nabla J(\theta )$，其中 $\alpha$ 是学习率。
4. 重复步骤 2 和 3 直到收敛。

公式：
$${\theta }_{t+1}={\theta }_t-\alpha \nabla J({\theta }_t)$$

用梯度下降发求解二次函数获取极值是的解
目标函数是一个简单的二次函数：

$$J(\theta )=(\theta -3{)}^2$$

这是一个抛物线形函数，其获取极小值时的解为 $\theta =3$。
示例代码：

import numpy as np
import matplotlib.pyplot as plt# 定义目标函数及其梯度
def J(theta):return (theta - 3)**2def gradient_J(theta):return 2 * (theta - 3)# 梯度下降法
def gradient_descent(initial_theta, learning_rate, iterations):theta = initial_thetahistory = []  # 用于保存每次迭代的参数和目标函数值for i in range(iterations):grad = gradient_J(theta)theta = theta - learning_rate * gradhistory.append((theta, J(theta)))print(f'Iteration {i+1}: theta = {theta}, J(theta) = {J(theta)}')return theta, history# 参数设置
initial_theta = 0.0
learning_rate = 0.1
iterations = 100# 求解
optimal_theta, history = gradient_descent(initial_theta, learning_rate, iterations)
print(f'Optimal theta: {optimal_theta}')# 绘制收敛过程
thetas, costs = zip(*history)
plt.plot(thetas, costs, '-o')
plt.xlabel('Theta')
plt.ylabel('J(Theta)')
plt.title('Convergence of Gradient Descent')
plt.show()

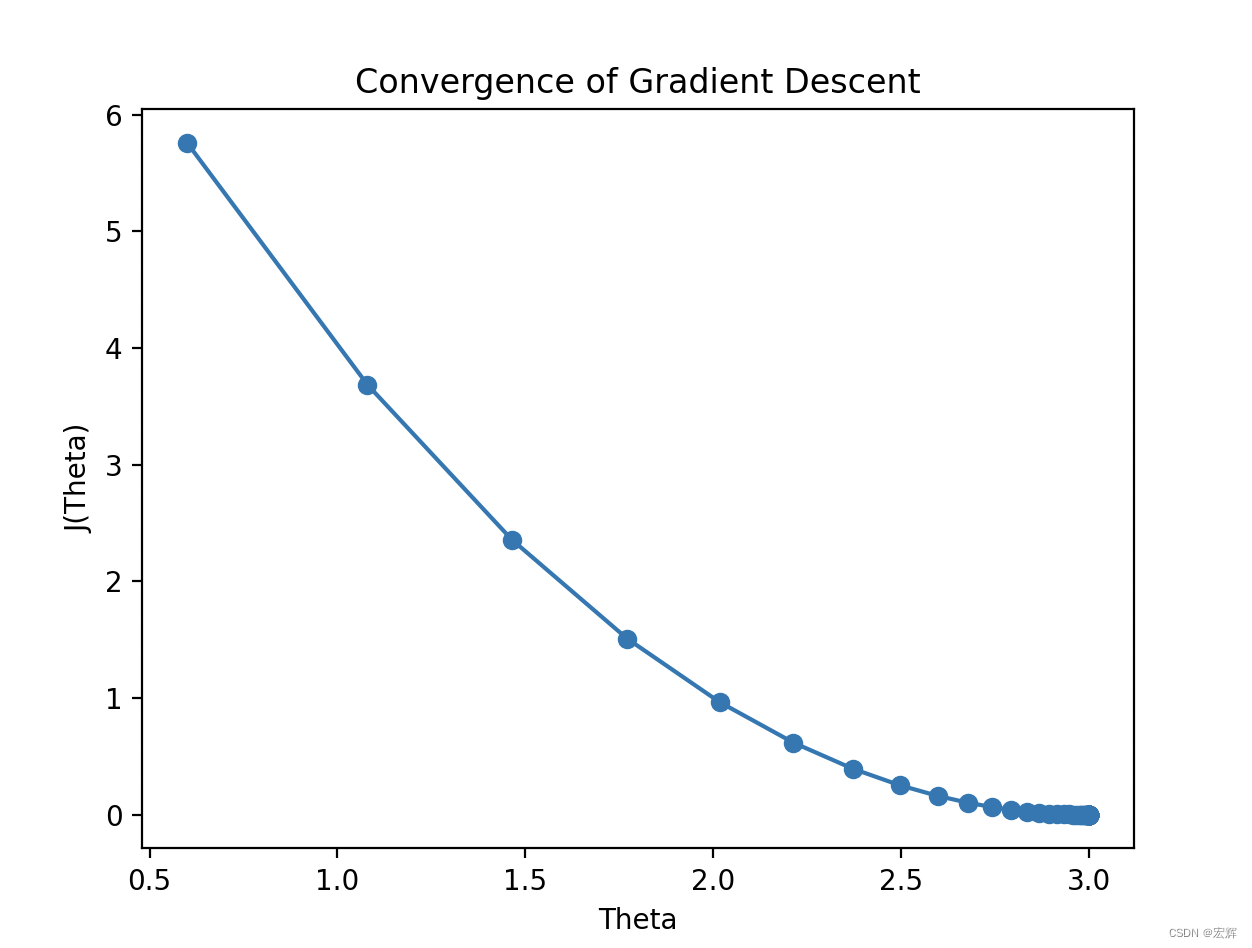
从图中可以看出，$Theta$随着步长的增加，$J(Theta)$不断接近最小值0。
循环100步时候，$Theta$=2.9999999993888893

7.2 牛顿法

牛顿法是一种用于求解非线性方程的迭代方法，通过泰勒展开近似来寻找函数的根，具有较快的收敛速度。

基本步骤：

1. 初始化值 $x_0$。
2. 计算函数 $f(x)$ 和导数 $f^{\prime }(x)$。
3. 更新值：$x_{n+1}=x_n-\frac{f(x_n)}{f^{\prime }(x_n)}$。
4. 重复步骤 2 和 3 直到收敛。

公式：
$$x_{n+1}=x_n-\frac{f(x_n)}{f^{\prime }(x_n)}$$

示例代码：

import numpy as np# 定义函数及其导数
def f(x):return x**2 - 2def df(x):return 2 * x# 牛顿法
def newton_method(initial_x, iterations):x = initial_xfor _ in range(iterations):x = x - f(x) / df(x)return x# 参数设置
initial_x = 1.0
iterations = 10# 求解
root = newton_method(initial_x, iterations)
print(f'Root: {root}')

7.3 Euler 法与 Runge-Kutta 法

Euler 法和 Runge-Kutta 法是数值求解常微分方程的基本方法。Euler 法简单但误差较大，而 Runge-Kutta 法通过更高阶的近似提高了精度。

7.3.1 Euler 法

公式：
$$y_{n+1}=y_n+hf(t_n,y_n)$$

示例代码：

import numpy as np
import matplotlib.pyplot as plt# 定义微分方程
def f(t, y):return t - y# Euler 法
def euler_method(f, t0, y0, h, n):t = np.zeros(n)y = np.zeros(n)t[0], y[0] = t0, y0for i in range(1, n):t[i] = t[i-1] + hy[i] = y[i-1] + h * f(t[i-1], y[i-1])return t, y# 参数设置
t0, y0 = 0, 1
h = 0.1
n = 100# 求解
t, y = euler_method(f, t0, y0, h, n)# 绘制结果
plt.plot(t, y, label='Euler method')
plt.xlabel('t')
plt.ylabel('y')
plt.legend()
plt.show()

7.3.2 Runge-Kutta 法

最常用的是四阶 Runge-Kutta 方法（RK4），具有较高的精度。

公式：
$$\begin{array}{rl}{k}_1& =hf(t_n,y_n)\\ k_2& =hf(t_n+\frac{h}{2},y_n+\frac{k_1}{2})\\ k_3& =hf(t_n+\frac{h}{2},y_n+\frac{k_2}{2})\\ k_4& =hf(t_n+h,y_n+k_3)\\ y_{n+1}& =y_n+\frac{1}{6}(k_1+2k_2+2k_3+k_4)\end{array}$$

示例代码：

import numpy as np
import matplotlib.pyplot as plt# 定义微分方程
def f(t, y):return t - y# Runge-Kutta 法
def runge_kutta_method(f, t0, y0, h, n):t = np.zeros(n)y = np.zeros(n)t[0], y[0] = t0, y0for i in range(1, n):t[i] = t[i-1] + hk1 = h * f(t[i-1], y[i-1])k2 = h * f(t[i-1] + h/2, y[i-1] + k1/2)k3 = h * f(t[i-1] + h/2, y[i-1] + k2/2)k4 = h * f(t[i-1] + h, y[i-1] + k3)y[i] = y[i-1] + (k1 + 2*k2 + 2*k3 + k4) / 6return t, y# 参数设置
t0, y0 = 0, 1
h = 0.1
n = 100# 求解
t, y = runge_kutta_method(f, t0, y0, h, n)# 绘制结果
plt.plot(t, y, label='Runge-Kutta method')
plt.xlabel('t')
plt.ylabel('y')
plt.legend()
plt.show()

7.4 Crank-Nicolson 法

Crank-Nicolson 法是一种用于求解偏微分方程（PDE）的隐式数值方法，具有较高的精度和稳定性。它是 Euler 法和中心差分法的组合，适用于时间和空间的二阶精度计算。

公式：
$$\frac{y_{n+1}-y_n}{h}=\frac{1}{2}\left(f(t_n,y_n)+f(t_{n+1},y_{n+1})\right)$$

示例代码：

import numpy as np
import matplotlib.pyplot as plt# 定义微分方程
def f(t, y):return t - y# Crank-Nicolson 法
def crank_nicolson_method(f, t0, y0, h, n):t = np.zeros(n)y = np.zeros(n)t[0], y[0] = t0, y0for i in range(1, n):t[i] = t[i-1] + hy_pred = y[i-1] + h * f(t[i-1], y[i-1])  # 预测y[i] = y[i-1] + (h / 2) * (f(t[i-1], y[i-1]) + f(t[i], y_pred))  # 校正return t, y# 参数设置
t0, y0 = 0, 1
h = 0.1
n = 100# 求解
t, y = crank_nicolson_method(f, t0, y0, h, n)# 绘制结果
plt.plot(t, y, label='Crank-Nicolson method')
plt.xlabel('t')
plt.ylabel('y')
plt.legend()
plt.show()

8.学习心得

本次学习了微分方程的基础概念，了解到公式推导和python编程求解两种方法求解微分方程，通过应用案例掌握了微分方程和差分方程题目的解题思路和编程技巧。

微分方程的求解有两种情况：求解解析解或者给定特定条件求解精确解（部分微分方程是没有解析解的）

• 通过SymPy 求解微分方程的解析式解；
• 通过Scipy的odeint或solve_ivp求精确解，其中solve_ivp 是 SciPy 库中较新的 ODE 求解器，提供了更多的灵活性和功能，支持多种算法。如果遇到高阶微分方程，要通过变元替换高阶项，使方程变成一阶方程再进行代码求解。

对于偏微分方程，python没有提供专门的解析包，需要更加实际情况编写代码求解。核心思想是将连续离散化处理！
为解决差分方程模型往往难以有效地模拟大多数离散模型问题，进而引入了元胞自动机模型

9. 对学习文档的一些疑问

9.1 文档2.1.4中梯型求解代码是否有误

此处的梯型法求解的代码有误，for循环中$Xn$初值应当为0，而不是0.7,以下是修改后的代码，仅供参考

def tixing():# 积分区间x0 = 0xn = 0.7# 步长n = 1000  # 分成1000个小区间h = (xn - x0) / ns = 0xn = 0 #此处先令xn为0，随循环逐渐递进for i in range(n):xn1 = xn + h;yn = f(xn)yn1 = f(xn1)s0 = (yn + yn1) * h / 2s += s0xn = xn1print(s)