Chapter 1 and 2
Fact
Facts: Facts are statements that areassumed to be true.
The dot ‘.’ character must come at the end of a fact.
Example: We want to tell “John likes Mary” : English interpretation
The standard form of fact in Prolog Likes (john, mary).
Rules
Rules: Rules are logical statements that describe the relationships between different facts.

Queries
Queries: That is, this query essentially asks something to Prolog:

Knowledge base 1 (example)
The facts and rules contained in a knowledge base are called clauses.
The end of a clause is marked with a full stop.

Expressing Conjunction

The comma “,” expresses conjunction (and) in Prolog
So, this rule says: ``Vincent plays air guitar if he listens to music and he is happy’

Knowledge base 5
KB5 contains four facts about the loves relation and one rule.

Prolog terms

Variable

“;” means “or” here , so this query means: are there any more women?
Atoms

complex terms

Arity(参数数量)
We can define two predicates with the same functor but with different arityProlog would treat this as two different predicates!
In Prolog documentation, arity of a predicate is usually indicated with the suffix “/” followed by a number to indicate the arity
for example:

Chapter 3 and 4
Truth table

Valuations
In propositional logic, a valuation corresponds to a single rowin the truth table.

Valid Inference
The inference from a finite set of premises p1, p2. . . pn-1, pn, to a conclusion q is a valid inference if for each valuation V with V(p1) = . . . = V(pn) = 1, also has that V(q) = 1.


Some famous valid inference:
- Modus Ponens: the way that affirms.
(p → q), p |= q. - Modus Tollens: the way that denies.
(p → q), ¬q |= ¬p.
More commonly used logical laws

Logical equivalence


- example
- 第二个用到上面的lagical laws

Chapter5
操作符之间的转换
- (p ↔q) is equivalence t o (p → q) ∧(q → p).
- (p → q ) is equivalence t o (¬p ∨q)
- (p ∧q ) is equivalence t o ¬(¬p ∨¬q)
- (p ∨q ) is equivalence to ¬(¬p ∧¬q)
a new operator (NAND)
**p | q ↔¬(p ∧q).**

Canonical Normal Forms
DNF(Disjunctive Normal Form)

CNF(Conjunctive Normal Form)

Chapter6
Library
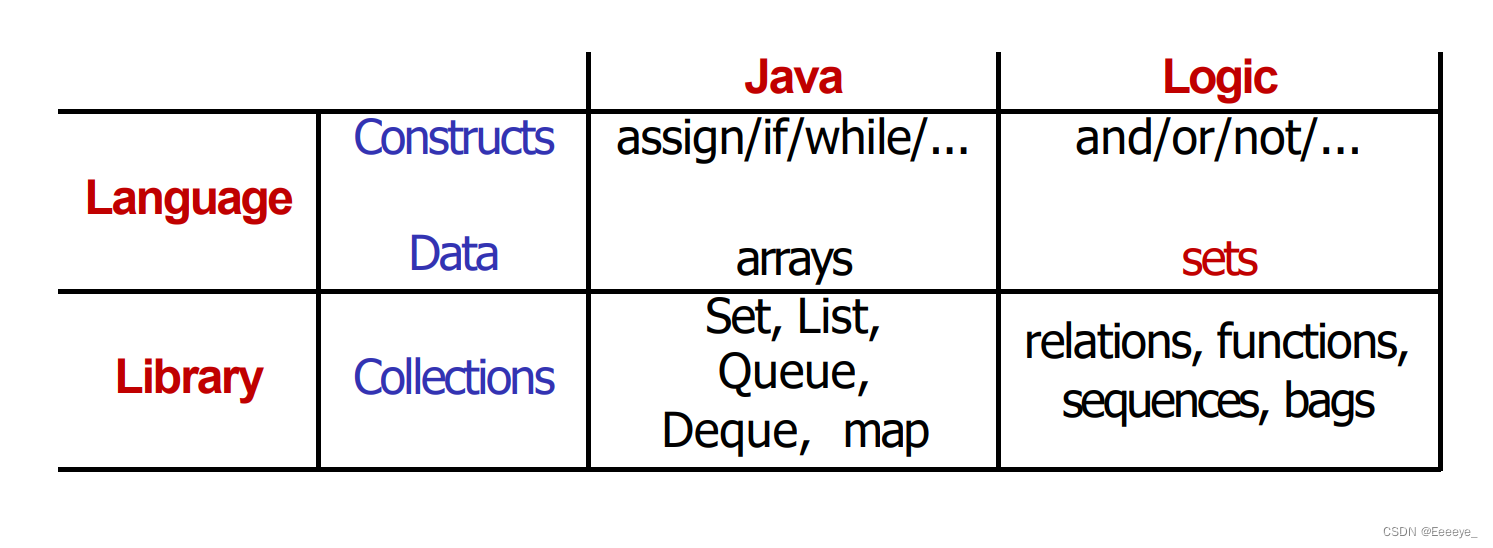
sets
- definition:‘A set is a collection of definite objects or numbers.”
- what can we do with sets?
- we can ask :" is x an element in the set of S?"
- we can’t ask:
Where is x in S (at the front, back, top, …)
How many times does x occur in S,…
- the way to define Set




点后是返回值
Comparing of sets:


Some examples:






——实现协程之间消息传递)







》)
事件管理系统源码(可自动生成鱼骨图))

)


