目录
1.经验熵
2.经验条件熵
3.信息增益
4.增益比率
5.例子1
6.例子2
在决策树模型中,我们会考虑应该选择哪一个特征作为根节点最好,这里就用到了信息增益
通俗上讲,信息增益就是在做出判断时,该信息对你影响程度的大小。比如你今天考虑要不要去郊游,你会考虑天气,距离,心情,是否空闲等等因素,非常纠结,但是如果信息中的天气显示今天暴雨,那大概率就不郊游了,那这个因素的信息增益就很强。

1.经验熵
Info(D)=-Σi=1...n(pilog2pi)
比如我们将一个立方体A抛向空中,记落地时着地的面为f1,f1的取值为{1,2,3,4,5,6},f1的熵entropy(f1)=-(1/6*log(1/6)+...+1/6*log(1/6))=-1*log(1/6)=2.58
- 信息熵描述随机变量的不确定性。
- 信息熵越小,信息的纯度越高,信息量就越少。
- 信息熵越大,信息的纯度越小,信息量就越多。
2.经验条件熵
在某一条件下,随机变量的不确定性。假设我们选择属性R作为分裂属性,数据集D中,R有k个不同的取值{V1,V2,...,Vk},于是可将D根据R的值分成k组{D1,D2,...,Dk},按R进行分裂后,将数据集D不同的类分开还需要的信息量为:
InfoR(D)=Σi=1...k(Di/D)Info(Di)
3.信息增益
在某一条件下,随机变量不确定性减少的程度。换句话说,信息增益代表了在一个条件下,信息复杂度(不确定性)减少的程度。那么我们现在也很好理解了,在决策树算法中,我们的关键就是每次选择一个特征,特征有多个,那么到底按照什么标准来选择哪一个特征。这个问题就可以用信息增益来度量。如果选择一个特征后,信息增益最大(信息不确定性减少的程度最大),那么我们就选取这个特征。
分裂前后,两个信息量只差:
Gain(R)=Info(D)-InfoR(D)
4.增益比率
信息增益选择方法有一个很大的缺陷,它总是会倾向于选择属性值多的属性,如果我们在上面的数据记录中加一个姓名属性,假设14条记录中的每个人姓名不同,那么信息增益就会选择姓名作为最佳属性,因为按姓名分裂后,每个组只包含一条记录,而每个记录只属于一类(要么购买电脑要么不购买,信息量计算为1/14(-1/1log1/1-0/1log0/1)*14=0,信息增益最大),因此纯度最高,以姓名作为测试分裂的结点下面有14个分支。但是这样的分类没有意义,它没有任何泛化能力。增益比率对此进行了改进,它引入一个分裂信息:
SplitInfoR(D)=-Σi=1...n(Di/D)log2(Di/D)
增益比率定义为信息增益与分裂信息的比率:
GainRatio(R)=Gain(R)/SplitInfoR(D)
我们找GainRatio最大的属性作为最佳分裂属性。如果一个属性的取值很多,那么SplitInfoR(D)会大,从而使GainRatio(R)变小。
不过增益比率也有缺点,SplitInfo(D)可能取0,此时没有计算意义;且当SplitInfo(D)趋向于0时,GainRatio(R)的值变得不可信,改进的措施就是在分母加一个平滑,这里加一个所有分裂信息的平均值:
GainRatio(R)=Gain(R)/(SplitInfo(D)+SplitInfoR(D))
5.例子1
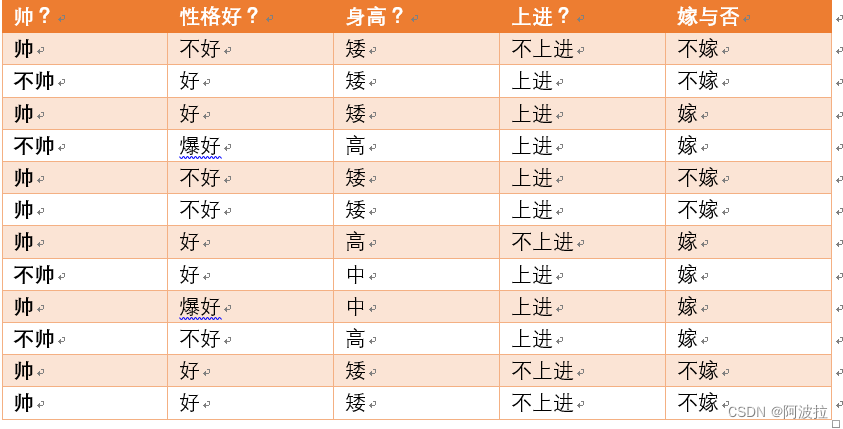
对于上述信息,可以求得随机变量X(嫁与不嫁)的信息熵为:
嫁的个数为6个,占1/2,那么信息熵为-1/2log1/2-1/2log1/2 = -log1/2=0.301
现在假如我知道了一个男生的身高信息。
身高有三个可能的取值{矮,中,高}
矮包括{1,2,3,5,6,11,12},嫁的个数为1个,不嫁的个数为6个
中包括{8,9} ,嫁的个数为2个,不嫁的个数为0个
高包括{4,7,10},嫁的个数为3个,不嫁的个数为0个
先回忆一下条件熵的公式如下:
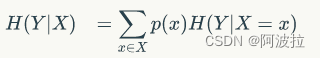
我们先求出公式对应的:
H(Y|X = 矮) = -1/7log1/7-6/7log6/7=0.178
H(Y|X=中) = -1log1-0 = 0
H(Y|X=高) = -1log1-0=0
p(X = 矮) = 7/12,p(X =中) = 2/12,p(X=高) = 3/12
则可以得出条件熵为:7/120.178+2/120+3/12*0 = 0.103
那么我们知道信息熵与条件熵相减就是我们的信息增益,为0.301-0.103=0.198
所以我们可以得出我们在知道了身高这个信息之后,信息增益是0.198
我们可以知道,本来如果我对一个男生什么都不知道的话,作为他的女朋友决定是否嫁给他的不确定性有0.301这么大。
当我们知道男朋友的身高信息后,不确定度减少了0.198.也就是说,身高这个特征对于我们广大女生同学来说,决定嫁不嫁给自己的男朋友是很重要的。
至少我们知道了身高特征后,我们原来没有底的心里(0.301)已经明朗一半多了,减少0.198了(大于原来的一半了)。
那么这就类似于非诚勿扰节目里面的桥段了,请问女嘉宾,你只能知道男生的一个特征。请问你想知道哪个特征。
假如其它特征我也全算了,信息增益是身高这个特征最大。那么我就可以说,我想知道男嘉宾的一个特征是身高特征。因为它在这些特征中,信息增益是最大的,知道了这个特征,嫁与不嫁的不确定度减少的是最多的。
来源:信息增益到底怎么理解呢?_南湖渔歌的博客-CSDN博客
6.例子2
| 记录ID | 年龄 | 收入层次 | 学生 | 信用等级 | 是否购买电脑 |
| 1 | 青少年 | 高 | 否 | 一般 | 否 |
| 2 | 青少年 | 高 | 否 | 良好 | 否 |
| 3 | 中年 | 高 | 否 | 一般 | 是 |
| 4 | 老年 | 中 | 否 | 一般 | 是 |
| 5 | 老年 | 低 | 是 | 一般 | 是 |
| 6 | 老年 | 低 | 是 | 良好 | 否 |
| 7 | 中年 | 低 | 是 | 良好 | 是 |
| 8 | 青少年 | 中 | 否 | 一般 | 否 |
| 9 | 青少年 | 低 | 是 | 一般 | 是 |
| 10 | 老年 | 中 | 是 | 一般 | 是 |
| 11 | 青少年 | 中 | 是 | 良好 | 是 |
| 12 | 中年 | 中 | 否 | 良好 | 是 |
| 13 | 中年 | 高 | 是 | 一般 | 是 |
| 14 | 老年 | 中 | 否 | 良好 | 否 |
1:计算Info(D)
Info(D)=-Σi=1...n(pilogpi)=-(5/14)log(5/14)-(9/14)log(9/14)=-0.3571*(-1.4856)-0.6429*(-0.6373)=0.1597+0.1234=0.5305+0.4097=0.9402
2:计算InfoR(D)
Info年龄(D)=(5/14)Info(D老年)+(4/14)Info(D中年)+(5/14)Info(D青少年)=(5/14)(-(3/5)log(3/5)-(2/5)log(2/5))+(4/14)(-(4/4)log(4/4)-(0/4)log(0/4))+(5/14)(-(2/5)log(2/5)-(3/5)log(3/5))
=(5/14)(0.6*0.737+0.4*1.3219)+(4/14)(0+0)+(5/14)(0.4*1.3219+0.6*0.737)
=(5/14)(0.4422+0.52876)+0+(5/14)(0.52876+0.4422)
=0.3571*0.97096+0+0.3571*0.97096
=0.694
同样可以计算出
Info收入层次(D)=0.911
Info学生(D)=0.789
Info信用等级(D)=0.892
3:计算信息增益:
Gain(年龄)=Info(D)-Info年龄(D)=0.940-0.694=0.246
Gain(收入层次)=Info(D)-Info收入层次(D)=0.940-0.911=0.029
Gain(学生)=Info(D)-Info学生(D)=0.940-0.789=0.151
Gain(信用等级)=Info(D)-Info信用等级(D)=0.940-0.892=0.058
4:计算分裂信息:
SplitInfo年龄(D)=-5/14log(5/14)-4/14log(4/14)-5/14log(5/14)=0.3571*1.4856+0.2857*1.8074+0.3571*1.4856=0.5305+0.5164+0.5305=1.5774
SplitInfo收入层次(D)=-4/14log(4/14)-6/14log(6/14)-4/14log(4/14)=0.2857*1.8074+0.4286*1.2223+0.2857*1.8074=0.5164+0.5139+0.5164=1.5467
SplitInfo学生(D)=-7/14log7/14-7/14log7/14=1
SplitInfo信用等级(D)=-6/14log(6/14)-8/14log(8/14)=0.4286*1.2223+0.5714*0.8074=0.5239+0.4613=0.9852
SplitInfo(D)=(SplitInfo年龄(D)+SplitInfo收入层次(D)+SplitInfo学生(D)+SplitInfo信用等级(D))/4=1.2773
5:计算增益比率:
GainRatio(年龄)=Gain(年龄)/(SplitInfo(D)+SplitInfo年龄(D))=0.246/(1.2773+1.5774)=0.0862
GainRatio(收入层次)=Gain(收入层次)/(SplitInfo(D)+SplitInfo收入层次(D))=0.029/(1.2773+1.5467)=0.0103
GainRatio(学生)=Gain(学生)/(SplitInfo(D)+SplitInfo学生(D))=0.151/(1.2773+1)=0.0663
GainRatio(信用等级)=Gain(信用等级)/(SplitInfo(D)+SplitInfo信用等级(D))=0.058/(1.2773+0.9852)=0.0256








。Javaee项目,ssm vue前后端分离项目。)

)







)
