import optimtool as oo
from optimtool.base import np, sp, plt
pip install optimtool >=2.4.2
无约束优化方法(optimtool.unconstrain)
import optimtool.unconstrain as ou
ou.[方法名].[函数名]([目标函数], [参数表], [初始迭代点])
f ( x ) = ∑ i = 1 n / 2 ( − 13 + x 2 i − 1 + ( ( 5 − x 2 i ) x 2 i − 2 ) x 2 i ) 2 + ( − 29 + x 2 i − 1 + ( ( x 2 i + 1 ) x 2 i − 14 ) x 2 i ) 2 , x 0 = [ 0.5 , − 2 , 0.5 , − 2 , . . . , 0.5 , − 2 ] . f(x)=\sum_{i=1}^{n/2}(-13+x_{2i-1}+((5-x_{2i})x_{2i}-2)x_{2i})^2+(-29+x_{2i-1}+((x_{2i}+1)x_{2i}-14)x_{2i})^2, x_0=[0.5, -2, 0.5, -2, ..., 0.5, -2]. f(x)=i=1∑n/2(−13+x2i−1+((5−x2i)x2i−2)x2i)2+(−29+x2i−1+((x2i+1)x2i−14)x2i)2,x0=[0.5,−2,0.5,−2,...,0.5,−2].
import optimtool.unconstrain as ou
x = sp.symbols("x1:5")
f = (-13 + x[0] + ((5 - x[1])*x[1] - 2)*x[1])**2 + \(-29 + x[0] + ((x[1] + 1)*x[1] - 14)*x[1])**2 + \(-13 + x[2] + ((5 - x[3])*x[3] - 2)*x[3])**2 + \(-29 + x[2] + ((x[3] + 1)*x[3] - 14)*x[3])**2
x_0 = (1, -1, 1, -1) # Random given
梯度下降法(gradient_descent)
ou.gradient_descent.[函数名]([目标函数], [参数表], [初始迭代点])
| 方法头 | 解释 |
|---|---|
| solve(funcs: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, epsilon: float=1e-10, k: int=0) -> OutputType | 通过解方程的方式来求解精确步长 |
| steepest(funcs: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“wolfe”, epsilon: float=1e-10, k: int=0) -> OutputType | 使用线搜索方法求解非精确步长(默认使用wolfe线搜索) |
| barzilar_borwein(funcs: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“Grippo”, c1: float=0.6, beta: float=0.6, M: int=20, eta: float=0.6, alpha: float=1, epsilon: float=1e-10, k: int=0) -> OutputType | 使用Grippo与ZhangHanger提出的非单调线搜索方法更新步长 |
ou.gradient_descent.barzilar_borwein(f, x, x_0, verbose=True)
(1, -1, 1, -1) 424.0 0
[ 1.0282111 -1.37928255 1.0282111 -1.37928255] 193.18208282562685 1
[ 1.04040867 -1.45642123 1.04040867 -1.45642123] 189.0040684546344 2
[ 1.04573189 -1.43382824 1.04573189 -1.43382824] 188.20259734914447 3
[ 1.05222391 -1.43478456 1.05222391 -1.43478456] 188.08207712135982 4
[ 1.21842112 -1.42548248 1.21842112 -1.42548248] 185.05873828867217 5
[ 2.13614312 -1.67393179 2.13614312 -1.67393179] 306.7394504286324 6
[ 2.13053183 -1.42904408 2.13053183 -1.42904408] 172.16897818349085 7
[ 2.13339147 -1.39448997 2.13339147 -1.39448997] 169.54142322335804 8
[ 2.13850418 -1.38626852 2.13850418 -1.38626852] 169.35850903892373 9
[ 2.14666499 -1.38571894 2.14666499 -1.38571894] 169.227056416181 10
[ 6.85105964 -1.21882377 6.85105964 -1.21882377] 119.64121168102085 11
[ 6.8498659 -0.82709031 6.8498659 -0.82709031] 219.03283073918098 12
[ 6.87286516 -1.13855733 6.87286516 -1.13855733] 114.81862255975581 13
[ 6.87787713 -1.15612617 6.87787713 -1.15612617] 114.57067950669307 14
[ 6.88112043 -1.1522921 6.88112043 -1.1522921 ] 114.53212856523825 15
[ 6.88723442 -1.15237179 6.88723442 -1.15237179] 114.4874731593348 16
[ 7.52073059 -1.08160888 7.52073059 -1.08160888] 111.60689603108094 17
[ 7.57812354 -1.50383598 7.57812354 -1.50383598] 306.84873605591366 18
[ 7.56259284 -1.10432895 7.56259284 -1.10432895] 110.06340620150246 19
[ 7.56525162 -1.11305159 7.56525162 -1.11305159] 109.911624361985 20
[ 7.56845044 -1.11585182 7.56845044 -1.11585182] 109.88443556709709 21
[ 7.57424656 -1.11514511 7.57424656 -1.11514511] 109.84842622986348 22
[ 8.11472065 -1.124156 8.11472065 -1.124156 ] 108.33148877567422 23
[ 8.11772403 -0.81394219 8.11772403 -0.81394219] 176.07597876873672 24
[ 8.13698116 -1.07860275 8.13698116 -1.07860275] 106.66200945891629 25
[ 8.14033875 -1.08558041 8.14033875 -1.08558041] 106.60960131271904 26
[ 8.14318086 -1.08408182 8.14318086 -1.08408182] 106.59292627568138 27
[ 8.15742491 -1.08445094 8.15742491 -1.08445094] 106.51940774009873 28
[ 8.48884737 -0.93560402 8.48884737 -0.93560402] 121.29547878113888 29
[ 8.51700355 -1.29748928 8.51700355 -1.29748928] 167.74917901005443 30
[ 8.50650818 -1.0447501 8.50650818 -1.0447501 ] 105.17130292526846 31
[ 8.50937365 -1.06118332 8.50937365 -1.06118332] 104.7825239343216 32
[ 8.51183986 -1.06396653 8.51183986 -1.06396653] 104.76340239835628 33
[ 8.51547867 -1.06364105 8.51547867 -1.06364105] 104.74639927086304 34
[ 9.69145476 -1.02322347 9.69145476 -1.02322347] 101.04132063991622 35
[ 9.69050332 -0.68561143 9.69050332 -0.68561143] 183.98629666416807 36
[ 9.71196065 -0.99177179 9.71196065 -0.99177179] 100.33437559015809 37
[ 9.71395331 -0.99691463 9.71395331 -0.99691463] 100.31205044592872 38
[ 9.71544113 -0.99582983 9.71544113 -0.99582983] 100.30702675123581 39
[ 9.72019742 -0.99588572 9.72019742 -0.99588572] 100.29410115962547 40
[ 9.96789324 -0.94002557 9.96789324 -0.94002557] 101.28390045346998 41
[ 9.98515667 -1.13463891 9.98515667 -1.13463891] 124.13069129617023 42
[ 9.97775526 -0.97677181 9.97775526 -0.97677181] 99.65833683277478 43
[ 9.97905436 -0.98038717 9.97905436 -0.98038717] 99.63998817758232 44
[ 9.98038184 -0.98072843 9.98038184 -0.98072843] 99.63682497083006 45
[ 9.99315753 -0.97962229 9.99315753 -0.97962229] 99.60739988195607 46
[10.72291903 -1.14038158 10.72291903 -1.14038158] 140.09339786064479 47
[10.71193259 -0.92569239 10.71193259 -0.92569239] 98.51338476293776 48
[10.71311599 -0.93659146 10.71311599 -0.93659146] 98.37085839829686 49
[10.71381956 -0.93806458 10.71381956 -0.93806458] 98.3680657249001 50
[10.71452791 -0.93800544 10.71452791 -0.93800544] 98.36725745304659 51
[11.12651334 -0.91557278 11.12651334 -0.91557278] 98.0388345985881 52
[11.14786066 -0.6544586 11.14786066 -0.6544586 ] 152.98071929318402 53
[11.1650964 -0.91655585 11.1650964 -0.91655585] 98.04252800378062 54
[11.16500654 -0.91067409 11.16500654 -0.91067409] 98.01952239829447 55
[11.16527568 -0.91147253 11.16527568 -0.91147253] 98.01882653662886 56
[11.16551336 -0.91145949 11.16551336 -0.91145949] 98.01873008878108 57
[11.40881542 -0.89699632 11.40881542 -0.89699632] 97.96852205445705 58
[11.41569897 -0.94570498 11.41569897 -0.94570498] 100.18347217648343 59
[11.41282871 -0.89647302 11.41282871 -0.89647302] 97.96860513443596 60
[11.41284758 -0.89679161 11.41284758 -0.89679161] 97.96850744492629 61
[11.41284808 -0.89680115 11.41284808 -0.89680115] 97.96850736241191 62
[11.41284802 -0.89680115 11.41284802 -0.89680115] 97.96850736240476 63
[11.41281318 -0.89680322 11.41281318 -0.89680322] 97.96850735944307 64
[11.41277898 -0.8968052 11.41277898 -0.8968052 ] 97.96850735848295 65
[11.4127827 -0.89686768 11.4127827 -0.89686768] 97.9685108985368 66
[11.41277899 -0.89680525 11.41277899 -0.89680525] 97.96850735848004 67
[11.41277899 -0.89680525 11.41277899 -0.89680525] 97.96850735848004 68
[11.41277899 -0.89680525 11.41277899 -0.89680525] 97.96850735848007 69
[11.41277899 -0.89680525 11.41277899 -0.89680525] 97.96850735848005 70
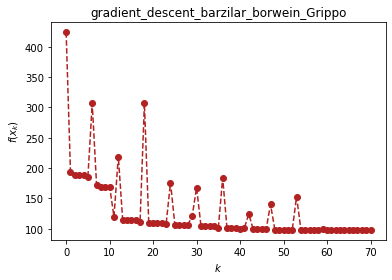
(array([11.41277899, -0.89680525, 11.41277899, -0.89680525]), 70)
牛顿法(newton)
ou.newton.[函数名]([目标函数], [参数表], [初始迭代点])
| 方法头 | 解释 |
|---|---|
| classic(funcs: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, epsilon: float=1e-10, k: int=0) -> OutputType | 通过直接对目标函数二阶导矩阵(海瑟矩阵)进行求逆来获取下一步的步长 |
| modified(funcs: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“wolfe”, m: int=20, epsilon: float=1e-10, k: int=0) -> OutputType | 修正当前海瑟矩阵保证其正定性(目前只接入了一种修正方法) |
| CG(funcs: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“wolfe”, eps: float=1e-3, epsilon: float=1e-6, k: int=0) -> OutputType | 采用牛顿-共轭梯度法求解梯度(非精确牛顿法的一种) |
ou.newton.CG(f, x, x_0, verbose=True)
(1, -1, 1, -1) 424.0 0
[-2.58333333 -1.41666667 -2.58333333 -1.41666667] 316.8589262366773 1
[11.66038408 -0.93093632 11.66038408 -0.93093632] 100.19046565464129 2
[11.37281532 -0.90000411 11.37281532 -0.90000411] 97.97044184270206 3
[11.41274925 -0.89680976 11.41274925 -0.89680976] 97.96850736600598 4
[11.41274911 -0.89680703 11.41274911 -0.89680703] 97.96850735921517 5
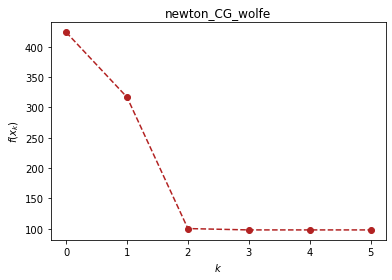
(array([11.41274911, -0.89680703, 11.41274911, -0.89680703]), 5)
拟牛顿法(newton_quasi)
ou.newton_quasi.[函数名]([目标函数], [参数表], [初始迭代点])
| 方法头 | 解释 |
|---|---|
| bfgs(funcs: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“wolfe”, epsilon: float=1e-10, k: int=0) -> OutputType | BFGS方法更新海瑟矩阵 |
| dfp(funcs: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“wolfe”, epsilon: float=1e-10, k: int=0) -> OutputType | DFP方法更新海瑟矩阵 |
| L_BFGS(funcs: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“wolfe”, m: float=6, epsilon: float=1e-10, k: int=0) -> OutputType | 双循环方法更新BFGS海瑟矩阵 |
ou.newton_quasi.bfgs(f, x, x_0, verbose=True)
(1, -1, 1, -1) 424.0 0
[-2.58333333 -1.41666667 -2.58333333 -1.41666667] 316.8589262367117 1
[-2.62231901 -1.41870216 -2.62231901 -1.41870216] 317.7181414041512 2
[12.34827743 -0.99197941 12.34827743 -0.99197941] 119.69430049634522 3
[10.38506302 -0.97660204 10.38506302 -0.97660204] 99.1887590330026 4
[11.1167875 -0.91944354 11.1167875 -0.91944354] 98.06444704676363 5
[11.406523 -0.89765767 11.406523 -0.89765767] 97.96874850140205 6
[11.41263195 -0.89681977 11.41263195 -0.89681977] 97.96850740648262 7
[11.41277931 -0.89680524 11.41277936 -0.89680524] 97.96850735848028 8
[11.41277892 -0.89680527 11.4127794 -0.89680523] 97.96850735848014 9
[11.41277892 -0.89680527 11.41277941 -0.89680523] 97.96850735848014 10
[11.41277899 -0.89680525 11.41277899 -0.89680525] 97.96850735848003 11
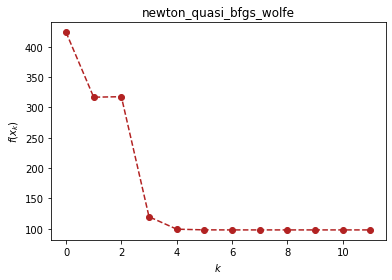
(array([11.41277899, -0.89680525, 11.41277899, -0.89680525]), 11)
非线性最小二乘法(nonlinear_least_square)
ou.nonlinear_least_square.[函数名]([目标函数], [参数表], [初始迭代点])
| 方法头 | 解释 |
|---|---|
| gauss_newton(funcr: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“wolfe”, epsilon: float=1e-10, k: int=0) -> OutputType | 高斯-牛顿提出的方法框架,包括OR分解等操作 |
| levenberg_marquardt(funcr: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, lamk: float=1, eta: float=0.2, p1: float=0.4, p2: float=0.9, gamma1: float=0.7, gamma2: float=1.3, epsk: float=1e-6, epsilon: float=1e-10, k: int=0) -> OutputType | Levenberg Marquardt提出的方法框架 |
r1, r2, x1, x2 = sp.symbols("r1 r2 x1 x2")
r1 = x1**3 - 2*x2**2 - 1
r2 = 2*x1 + x2 - 2
ou.nonlinear_least_square.gauss_newton((r1, r2), (x1, x2), (1, 1), verbose=True)
(1, 1) 2.5 0
[0.81818182 0.36363636] 0.2568683776624116 1
[0.96394194 0.07211612] 0.006580566252158881 2
[0.99803991 0.00392018] 1.7401957457499415e-05 3
[9.99993633e-01 1.27332936e-05] 1.824077317348686e-10 4
[1.00000000e+00 1.35111426e-10] 2.053700029739614e-20 5
[1.00000000e+00 6.08502493e-21] 1.8513764194952984e-41 6
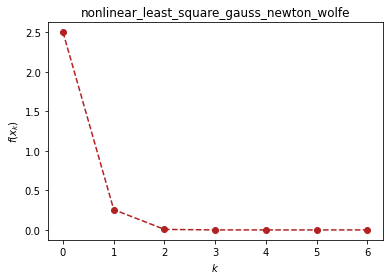
(array([1.00000000e+00, 6.08502493e-21]), 6)
信赖域方法(trust_region)
ou.trust_region.[函数名]([目标函数], [参数表], [初始迭代点])
| 方法头 | 解释 |
|---|---|
| steihaug_CG(funcs: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, r0: float=1, rmax: float=2, eta: float=0.2, p1: float=0.4, p2: float=0.6, gamma1: float=0.5, gamma2: float=1.5, epsk: float=1e-6, epsilon: float=1e-6, k: int=0) -> OutputType | 截断共轭梯度法在此方法中被用于搜索步长 |
ou.trust_region.steihaug_CG(f, x, x_0, verbose=True)
(1, -1, 1, -1) 424.0 0
[ 1.37436693 -1.59987449 1.37436693 -1.59987449] 234.85673849734079 1
[ 2.41674356 -1.40378533 2.41674356 -1.40378533] 166.3039476276758 2
[ 3.82788408 -1.31060572 3.82788408 -1.31060572] 145.04222337248802 3
[ 5.2400307 -1.23417328 5.2400307 -1.23417328] 128.87290397464753 4
[ 6.65278513 -1.16994762 6.65278513 -1.16994762] 116.28517783715984 5
[ 8.06468738 -1.08912665 8.06468738 -1.08912665] 107.0112703070541 6
[ 9.47634365 -1.00411738 9.47634365 -1.00411738] 101.03664220216237 7
[10.88855469 -0.92888453 10.88855469 -0.92888453] 98.19478501142473 8
[11.4157009 -0.89681743 11.4157009 -0.89681743] 97.96854545237576 9
[11.41277892 -0.89680526 11.41277892 -0.89680526] 97.96850735848007 10
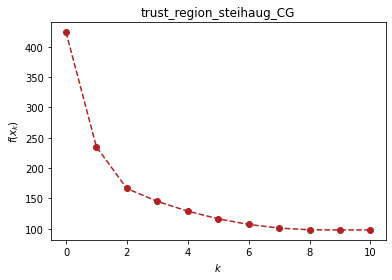
(array([11.41277892, -0.89680526, 11.41277892, -0.89680526]), 10)


-- fonts - 字体库)

激光线扫描-位移台标定)












)

