系列上文:傅里叶系列 P1 的定价选项_无水先生的博客
一、说明
- 如果您想了解更多关于傅里叶级数基础知识的信息,请查看第 1 部分。
- 随附笔记本:Github
- 本文基于我在阿姆斯特丹大学由Michel Vellekoop教授指导的随机微积分(2023)课程的笔记。
- 查看第 3 部分:链接
内容:
- 傅里叶余弦展开
- S(T)的密度函数
- 余弦的欧拉公式
- 特征函数 — 几何布朗运动的特征函数。
- 期权定价公式
- N项的收敛性和选择良好限值的重要性
- 分析解决方案的误差分析
“对他来说没有什么不可能的”
亚历山大大帝
二、傅里叶余弦展开
与正弦-余弦展开类似,我们可以只用等式的余弦部分做同样的事情:
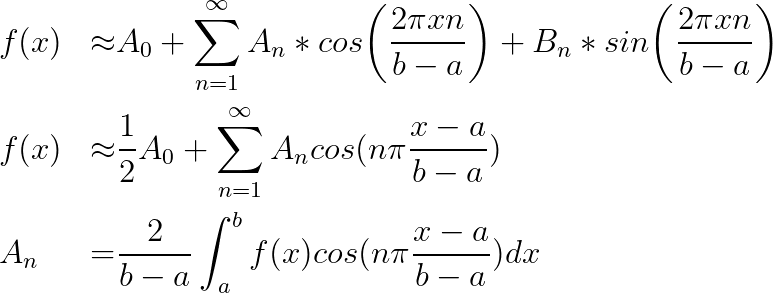
从余弦-正弦变换到余弦变换
你可以从下面的函数中看到,我们在第 1 部分中也做了,余弦能够很好地近似相同的函数
def get_fourier_approx(f, x:np.array, a:float, b:float, N:int):fa = lambda x, n : f(x) * cos((2*pi*n*x)/(b - a))fb = lambda x, n : f(x) * sin((2*pi*n*x)/(b - a))A0 = 1/(b - a) * quad(f, a, b, limit=200)[0]Cosine_Sine_Sum = np.zeros_like(x)for n in range(1, N+1):A = 2/(b - a) * quad(fa, a, b, args=(n), limit=200)[0]B = 2/(b - a) * quad(fb, a, b, args=(n), limit=200)[0]Cosine_Sine_Sum += A*cos((2*pi*n*x)/(b - a)) + B*sin((2*pi*n*x)/(b - a))fx = A0 + Cosine_Sine_Sumreturn fxmean = 100
std = .1 *sqrt(5)*100
f = lambda x : (1/(std*sqrt(2*pi))) * exp(-(x-mean)**2/(2*std**2)) #*12/0.0175a = mean - 12 * std
b = mean + 12 * std
方形功能 — 来源:笔记本

线路功能 — 来源:笔记本
正态分布 — 来源:笔记本
Avg Residuals
N Square f Line f Normal Distribution
8 1.311711 0.447389 1.593045e-04
16 0.784683 0.264635 1.214211e-07
32 0.440387 0.153540 7.100142e-18
64 0.268449 0.088745 3.628299e-14
128 0.154604 0.052147 2.992953e-12 议论
- 结论与第 1 部分相同,正态分布非常拟合,我们需要在值 [a, b] 中取足够的范围
- 由于仅使用余弦部分。它简化了我们必须做的许多后续步骤,并加快了该过程,因为我们必须计算更少的东西。
三、S(T)的密度函数
要开始获得对问题的直觉,我们必须解决,最好从制作一个函数及其傅里叶变换开始,给定一些初始值,S0,T,r,sigma,它计算S_T = X的概率。

S(T)密度函数的计算方法
需要注意的是,[-12 西格玛,12 西格玛] 的区间涵盖 99。再加上另外 33 个 9!有人可能会说这是极端的,但使用高西格玛很重要,这样密度函数就涵盖了深度的价外选择。(我稍后会回到那个)
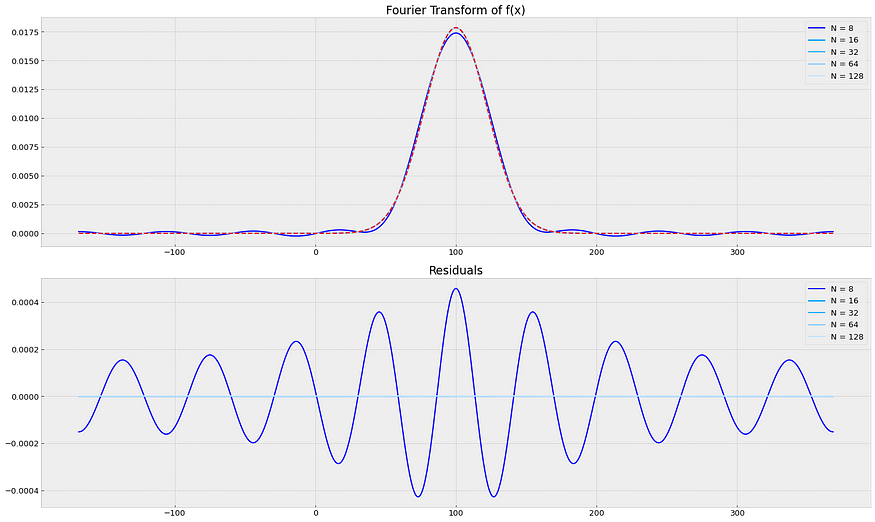
S(T) 的密度函数,S0=100, T=5Y, r=5%, sigma=10% — 来源: 笔记本
N Avg Residual
8 1.897794e-02
16 7.159815e-03
32 5.616416e-04
64 2.326956e-06
128 1.384069e-10 四、傅里叶级数的定价选项
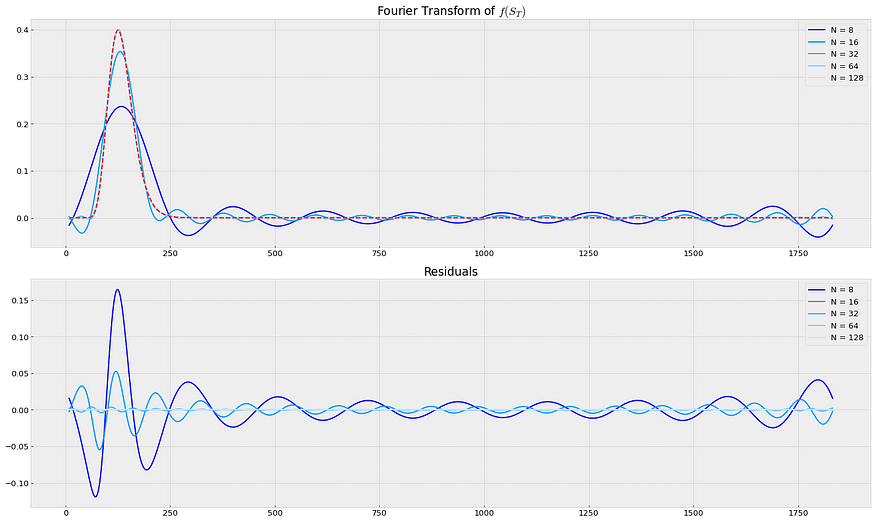
4.1 第 1 步:变换 cos(x) 的欧拉公式
我们将通过使用欧拉公式变换 cos(x) 来开始推导一个函数的旅程,以使用傅里叶级数为期权定价。这将有助于我们必须做的后续步骤。
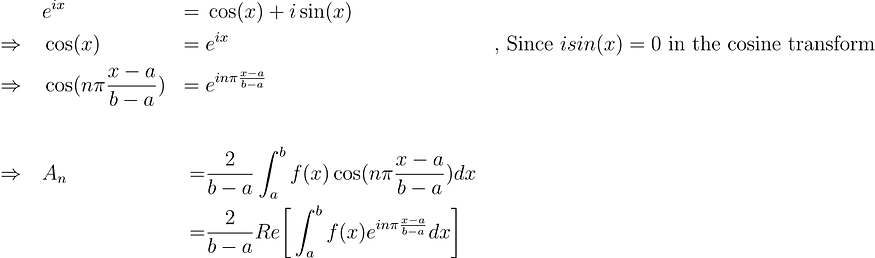
4.2 第 2 步:随机变量的特征函数
在概率论中,特征函数是为随机变量定义的复值函数。它捕获随机变量的矩和分布属性,允许使用傅里叶变换等技术分析各种统计属性。例如,对于正态分布或泊松分布之后的随机变量:
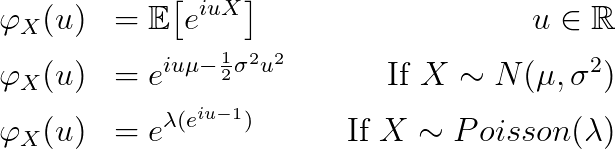
随机变量的特征函数
4.3 步骤3:使用特征函数对积分进行解析解
在我们的用例中,我们可以转换 log(S_T) 的密度函数。结合步骤 1 继续从 A 的步骤 2 转换 f(x),并知道 f(x) 是具有已知特征函数的随机变量的密度:
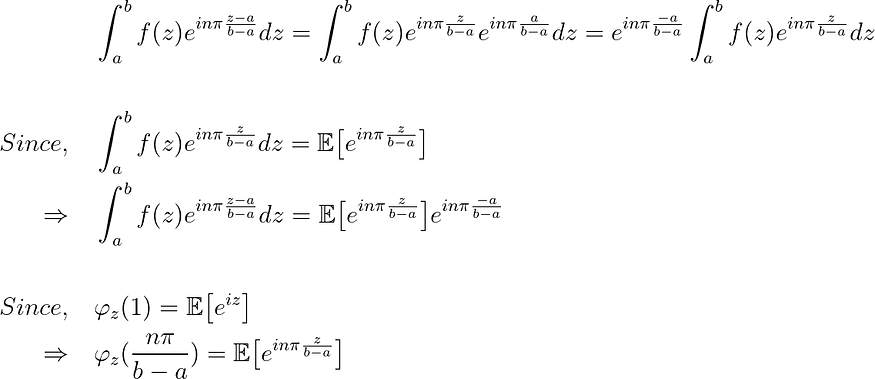
知道我们可以将积分转换为特征函数,使我们能够显式计算积分,我之前用 scipy 的四边形在数值上所做的。假设期望值为 [a, b] 的足够大的区间,因为 f(z) 是随机变量的密度函数。
第 4 步:将它们捆绑在一起以显式计算 A 系数
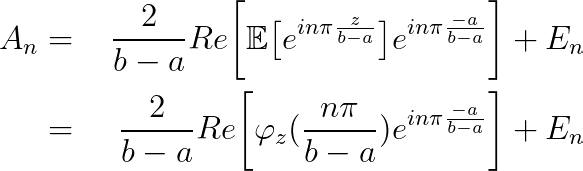
其中 En 是 [a,b] 外部积分的一部分,如果对于概率质量 f(x),我们选择 a,b,其中 f(x) 接近于零(对于正态±12sigma),则非常小。如果 f(x) 是期权的收益,并且 a,b 的收益非常小,则可以应用类似的概念
def Fourier_cosine_char_function(char_function, x:np.array, a, b, N:int):A = lambda n : 2/(b-a) * np.real( char_function((n*pi)/(b-a))*exp((-1j*n*pi*a)/(b-a)) )fx = .5*A(0)for n in range(1, N+1):fx += A(n) * cos(n*pi * (x-a)/(b-a))return fxS0 = 100
K = 100
r = 0.05
sigma = 0.1
T = 5.0# For normal distribution
mu = 100
sigma = 25
char_function = lambda u: exp(1j*u*mu -.5*sigma**2*u**2)
f = lambda x: norm.pdf(x, loc=mu, scale=sigma)a = 100 - 12 * sigma
b = 100 + 12 * sigma
使用具有特征函数的显式解的正态分布的密度 - 来源:笔记本
N Avg. Residual Execution Time
8 1.182498e-03 0.000059
16 1.588727e-04 0.000092
32 1.160981e-07 0.000180
64 2.983220e-18 0.000358
128 2.986019e-18 0.000767 4.4 评论
- 如您所见,我们做得很好。执行时间很短,我们只需要 32 个项即可快速收敛
- 使用特征函数可提高傅里叶级数近似的精度,并使计算更简单。
- 使用 cos 的虚数变换,我们可以将系数中的积分转换为密度函数的特征函数。
五、使用傅里叶级数的期权定价
5.1 第 1 步:回顾
对于表示随机变量 z 的密度函数的函数 f,我们有傅里叶余弦展开:
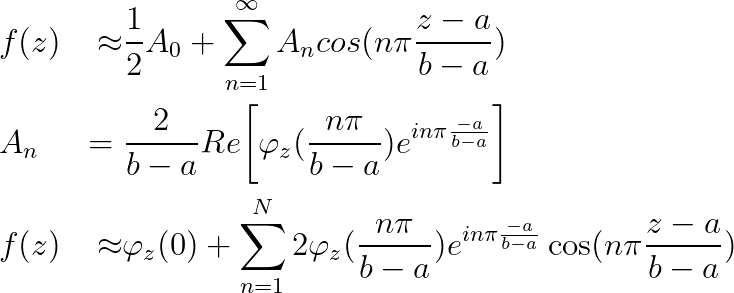
具有已知特征函数的随机变量z的密度函数
5.2 第二步:未来资产价格密度的特征函数
当我们为资产定价时,我们有一个资产价值对数的密度函数,它接受参数:t、T、S(t)、r、sigma,并输出 S(T) 的概率。在随机微积分中,根据上一节的步骤 2 计算随机变量的特征函数是很简单的。我们将使用这个新工具来为具有定义收益 F(T, S_T) 的衍生品 F 定价:
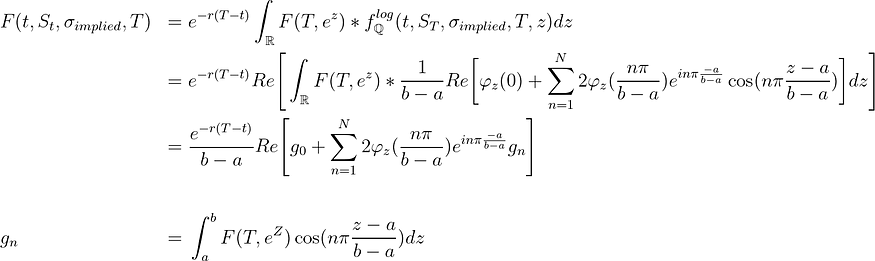
计算在 T 处具有已知收益的衍生品价格的公式
我上面所做的步骤是:
- 在 T 处贴现导数的预期收益值(第 1 行)
- 用我们上面推导的傅里叶级数变换代替密度函数。(第 2 行)
- 分离包含 z 的项并将它们打包为系数 gn
5.3 第 3 步:解析求解 g(n)
由于 gn 中的积分是针对 T 处的值,如果收益函数是显式的,我们可以分析计算积分。在这种情况下,我们将尝试以最大收益{K-S(T), 0}为欧洲看跌期权定价。因此:

Gn系数的解析解
要获得此处显示的解,您可以使用在线定积分计算器,对于 g0,您将使用 gn 的极限,因为 n 接近 0 以获得解,因为替换 n=0 意味着无法定义 g0。
5.4 第 4 步:GBM 特征函数
现在我们有了“武器”,我们只会错过子弹。在这种情况下,假设随机变量 z 遵循 Q 下的几何布朗运动。具有特征功能的“子弹”:
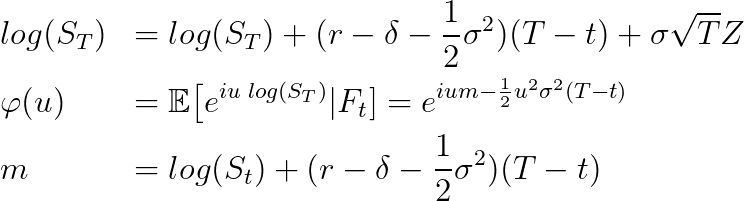
几何布朗运动的特征函数
def Fourier_BS_Put(S0, K, T, sigma, r, N):_sigma, _T = max(.1, sigma), max(1, T)a = log(S0) + r * _T - 12 * _sigma * np.sqrt(_T) # Upper limit -12 std from the expected valueb = log(S0) + r * _T + 12 * _sigma * np.sqrt(_T) # Lower limit -12 std from the expected valueh = lambda n : (n*pi) / (b-a) g = lambda n : (exp(a) - (K/h(n))*sin(h(n)*(a - log(K))) - K*cos(h(n)*(a - log(K)))) / (1 + h(n)**2)g0 = K*(log(K) - a - 1) + exp(a)m = log(S0) + (r - .5*sigma**2)*(T)gbm_char= lambda u : exp(1j * u * m -0.5*(u**2 * sigma**2)*T)F = g0 for n in range(1, N+1):h_n = h(n)F += 2*bs_char(h_n) * exp(-1j*a*h_n) * g(n)F = exp((-r*T))/(b-a) * np.real(F)return F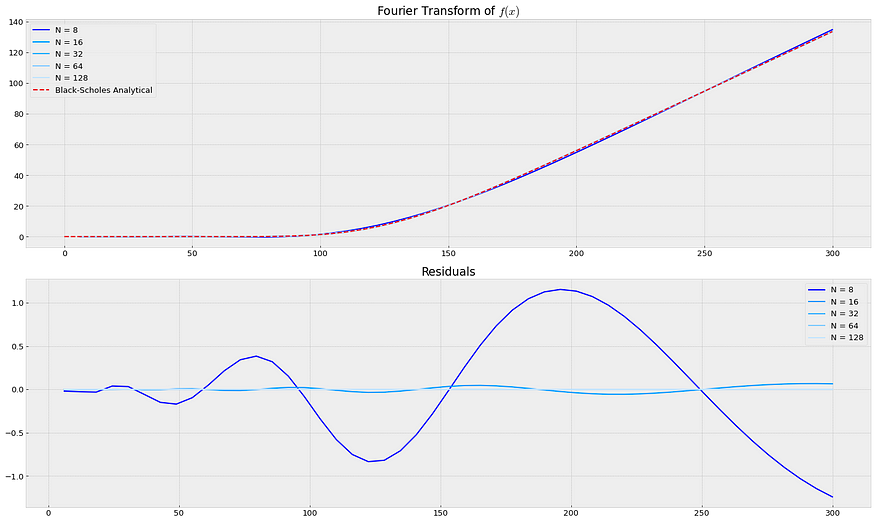
期权相对于不同执行价格的价格。S0=100, T=5Y, r=5%, 西格玛=10% — 来源: 笔记本
N avg_residuals Ex. Time
8 5.075343e-01 0.000185
16 2.556765e-02 0.000179
32 5.810656e-06 0.000265
64 2.319065e-14 0.000461
128 2.319066e-14 0.000787 5.5 评论
- 这种方法被证明是计算欧洲看跌期权价值的一种非常快速有效的方法
- 我们控制的唯一影响近似误差的因素是 N、项数和我们查看的 S(T) 值的区间 [a, b]。
六、选择正确的限制 [a, b]
下图说明了人们在使用傅里叶级数时需要了解的 2 件非常重要的事情。
1. 限制 [a=S_T(-z_score), b=S_T(z_score)] 需要涵盖所有可能的执行价格
2.随着西格玛的增加,近似误差也会增加

正确选择分布极限的图示以及近似误差如何随着较大的西格马而增加 — 来源:笔记本
在第一个子图中,您可以看到,如果我们的执行价格为 S(T) = 600,我们将无法正确定价,因为我们仅模拟了 S(-12) 到 S(12) 的值。因此,您可以在第二幅图中看到,这种执行价格的价值将非常错误!
在第三幅图中,您可以看到涵盖各种执行价格的西格玛。但是,由于收益的形状,很难用相同数量的项准确近似函数。因此,随着西格玛的增加,您可能需要增加项 N 的数量。
第一个子图的平均误差为:7.676e-12 第一个子图的平均误差为:2.830e-02
第一个子图的平均误差为:1.405e-03
*对于 N = 128
七、不同项数 N 的近似误差

近似欧洲看跌期权的解析解时出错 — 来源:笔记本
我做了一个简单的实验,看看如何在不同数量的术语上减少误差。您可以看到,我们有一个指数收敛,而计算成本是线性的。每个计算科学家的梦想。这意味着,当我们用赫斯顿模型替换特征函数时,我们不必付出蒙特卡罗数值积分的代价,其中误差随 N 的平方根而减小。
八、欧洲看跌期权所有可能输入值的错误分析
价值 100 欧元的股票。我模拟了看跌期权的定价条件,其中:
K = [0, 500]T = [0, 30Y]r = [-3%, 20%]sigma = [0.5%, 100%]
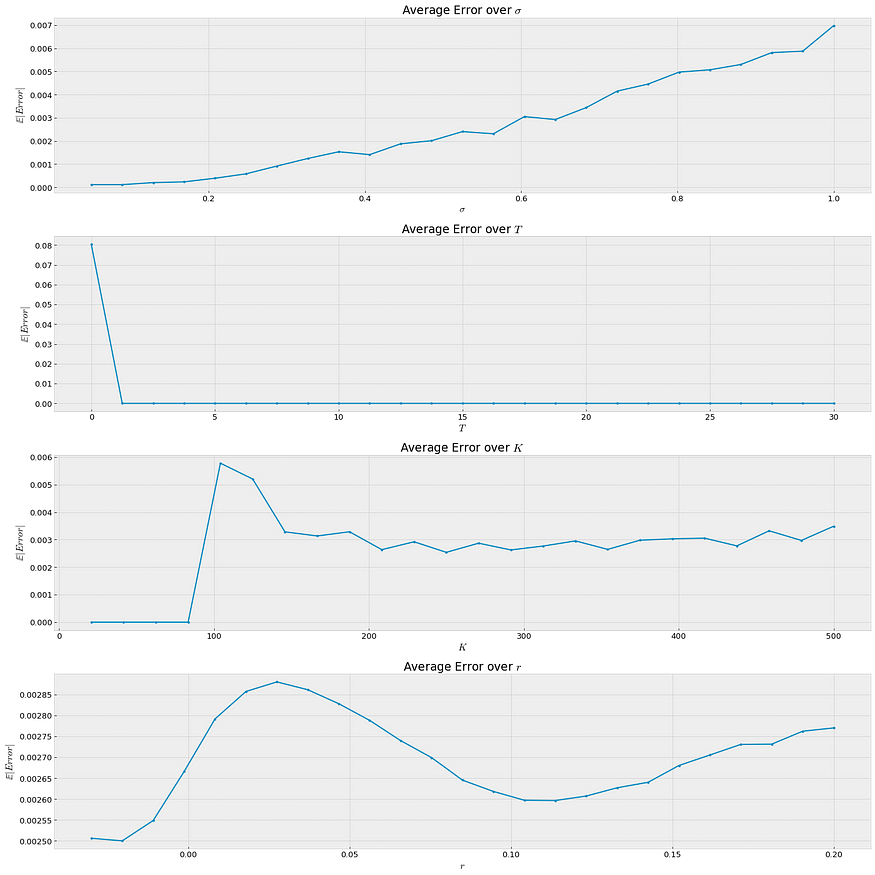
不同参数值的平均误差可视化 — 来源:笔记本
评论:
- 似乎对于到期 T=0 的期权,近似值增加了误差,但这归因于已知的收益,这是我在文章开头展示的线函数,它比曲线函数更具近似性。为了解决这个问题,可以使用更多的术语。
- Sigma 与近似误差呈线性关系,因为它将函数的形状更改为更难近似的形状。(如我之前所示)同样,为了解决这个问题,可以使用更多的术语。
总平均误差:0.00289 EUR,在我之前定义的所有给定值 K、T、r 和 sigma 范围内。
九、结论
我逐步解释了如何从一般的傅里叶变换转向用于计算欧洲看跌期权收益的定制函数。
但是,如果您想为收益不依赖于固定间隔的衍生品定价,则必须使用更复杂的数值技术。比如有限差分,或者蒙特卡洛。
尽管到目前为止这是一个“无用”的工具,但我们为使用Heston模型的定价选项奠定了基础,我们无法进行分析。希望您可以使用相同的原则进行定价选项
我希望您发现这篇文章有用,我希望在第 3/3 部分见到您,我们将看到如何将赫斯顿模型与傅里叶级数一起使用以及如何在期权链上校准它。






激光线扫描-光平面标定)







)





