1.函数、函数的傅里叶级数展开、傅里叶级数的和函数之间的关系
1.1 傅里叶级数中的系数公式推导
我们先来推导一下傅里叶级数中的系数公式,其实笔者已经写过一篇相关笔记,详见:为什么要把一个函数分解成三角函数?(傅利叶级数)



f ( x ) ∼ a 0 2 + ∑ n = 1 ∞ ( a n cos n π x l + b n sin n π x l ) ( x ∈ R ) f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n cos n π x l + b n sin n π x l ) ( − l < x < l ) a 0 = 1 l ∫ − l l f ( x ) d x = 2 l ∫ 0 l f ( x ) d x a n = 1 l ∫ − l l f ( x ) cos n π x l d x = 2 l ∫ 0 l f ( x ) cos n π x l d x b n = 1 l ∫ − l l f ( x ) sin n π x l d x = 2 l ∫ 0 l f ( x ) sin n π x l d x f(x)\sim \frac{a_0}{2}+\sum\limits_{n=1}^{\infty}(a_n\cos\frac{n\pi x}{l}+b_n\sin\frac{n\pi x}{l})(x\in \boldsymbol{R})\\ ~\\ f(x)= \frac{a_0}{2}+\sum\limits_{n=1}^{\infty}(a_n\cos\frac{n\pi x}{l}+b_n\sin\frac{n\pi x}{l})(-l\lt x\lt l)\\ ~\\ a_0=\frac{1}{l}\int_{-l}^{l}f(x)dx=\frac{2}{l}\int_{0}^{l}f(x)dx\\ ~\\ a_n=\frac{1}{l}\int_{-l}^{l}f(x)\cos\frac{n\pi x}{l}dx=\frac{2}{l}\int_{0}^{l}f(x)\cos\frac{n\pi x}{l}dx\\ ~\\ b_n=\frac{1}{l}\int_{-l}^{l}f(x)\sin\frac{n\pi x}{l}dx=\frac{2}{l}\int_{0}^{l}f(x)\sin\frac{n\pi x}{l}dx f(x)∼2a0+n=1∑∞(ancoslnπx+bnsinlnπx)(x∈R) f(x)=2a0+n=1∑∞(ancoslnπx+bnsinlnπx)(−l<x<l) a0=l1∫−llf(x)dx=l2∫0lf(x)dx an=l1∫−llf(x)coslnπxdx=l2∫0lf(x)coslnπxdx bn=l1∫−llf(x)sinlnπxdx=l2∫0lf(x)sinlnπxdx
如果上述公式中 l = π l=\pi l=π
f ( x ) ∼ a 0 2 + ∑ n = 1 ∞ ( a n cos n x + b n sin n x ) ( x ∈ R ) f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n cos n x + b n sin n x ) ( − π < x < π ) a 0 = 1 π ∫ − π π f ( x ) d x = 2 π ∫ 0 π f ( x ) d x a n = 1 π ∫ − π π f ( x ) cos n x d x = 2 π ∫ 0 π f ( x ) cos n x d x b n = 1 π ∫ − π π f ( x ) sin n x d x = 2 π ∫ 0 π f ( x ) sin n x d x f(x)\sim \frac{a_0}{2}+\sum\limits_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)(x\in \boldsymbol{R})\\ ~\\ f(x)= \frac{a_0}{2}+\sum\limits_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)(-\pi\lt x\lt \pi)\\ ~\\ a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx=\frac{2}{\pi}\int_{0}^{\pi}f(x)dx\\ ~\\ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx=\frac{2}{\pi}\int_{0}^{\pi}f(x)\cos nxdx\\ ~\\ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx=\frac{2}{\pi}\int_{0}^{\pi}f(x)\sin nxdx f(x)∼2a0+n=1∑∞(ancosnx+bnsinnx)(x∈R) f(x)=2a0+n=1∑∞(ancosnx+bnsinnx)(−π<x<π) a0=π1∫−ππf(x)dx=π2∫0πf(x)dx an=π1∫−ππf(x)cosnxdx=π2∫0πf(x)cosnxdx bn=π1∫−ππf(x)sinnxdx=π2∫0πf(x)sinnxdx
1.2将函数展开为傅里叶级数
2008年数一
将函数 f ( x ) = 1 − x 2 ( 0 ≤ x ≤ π ) f(x)=1-x^2(0\leq x\leq \pi) f(x)=1−x2(0≤x≤π) 展开成余弦形式的傅里叶级数,并求级数 ∑ n = 1 ∞ ( − 1 ) n − 1 n 2 \sum\limits_{n=1}^{\infty}\frac{(-1)^{n-1}}{n^2} n=1∑∞n2(−1)n−1的和
由于展开成余弦形式的傅里叶级数,故不含正弦级数且 b n = 0 b_n=0 bn=0
f ( x ) ∼ a 0 2 + ∑ n = 1 ∞ a n cos n x ( x ∈ R ) f ( x ) = a 0 2 + ∑ n = 1 ∞ a n cos n x ( − π ≤ x ≤ π ) a 0 = 1 π ∫ − π π 1 − x 2 d x = 2 π ∫ 0 π 1 − x 2 d x = 2 ( 1 − π 2 3 ) a n = 1 π ∫ − π π ( 1 − x 2 ) cos n x d x = 2 π ∫ 0 π ( 1 − x 2 ) cos n x d x = ( − 1 ) n + 1 ⋅ 4 n 2 f(x)\sim \frac{a_0}{2}+\sum\limits_{n=1}^{\infty}a_n\cos nx(x\in \boldsymbol{R})\\ ~\\ f(x)= \frac{a_0}{2}+\sum\limits_{n=1}^{\infty}a_n\cos nx(-\pi\leq x\leq \pi)\\ ~\\ a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}1-x^2dx=\frac{2}{\pi}\int_{0}^{\pi}1-x^2dx=2(1-\frac{\pi^2}{3})\\ ~\\ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}(1-x^2)\cos nxdx=\frac{2}{\pi}\int_{0}^{\pi}(1-x^2)\cos nxdx=\frac{(-1)^{n+1}\cdot4}{n^2} f(x)∼2a0+n=1∑∞ancosnx(x∈R) f(x)=2a0+n=1∑∞ancosnx(−π≤x≤π) a0=π1∫−ππ1−x2dx=π2∫0π1−x2dx=2(1−3π2) an=π1∫−ππ(1−x2)cosnxdx=π2∫0π(1−x2)cosnxdx=n2(−1)n+1⋅4
f ( x ) = 1 − π 2 3 + ∑ n = 1 ∞ ( − 1 ) n + 1 ⋅ 4 n 2 cos n x ( − π ≤ x ≤ π ) f ( 0 ) = 1 − π 2 3 + 4 ∑ n = 1 ∞ ( − 1 ) n + 1 n 2 ( − π ≤ x ≤ π ) f ( 0 ) = 1 − 0 2 = 1 1 = 1 − π 2 3 + 4 ∑ n = 1 ∞ ( − 1 ) n + 1 n 2 ( − π ≤ x ≤ π ) ∑ n = 1 ∞ ( − 1 ) n + 1 n 2 = π 2 12 f(x)= 1-\frac{\pi^2}{3}+\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}\cdot4}{n^2}\cos nx(-\pi\leq x\leq \pi)\\ ~\\ f(0)=1-\frac{\pi^2}{3}+4\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{n^2}(-\pi\leq x\leq \pi)\\ ~\\ f(0)=1-0^2=1\\ ~\\ 1=1-\frac{\pi^2}{3}+4\sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{n^2}(-\pi\leq x\leq \pi)\\ ~\\ \sum\limits_{n=1}^{\infty}\frac{(-1)^{n+1}}{n^2}=\frac{\pi^2}{12} f(x)=1−3π2+n=1∑∞n2(−1)n+1⋅4cosnx(−π≤x≤π) f(0)=1−3π2+4n=1∑∞n2(−1)n+1(−π≤x≤π) f(0)=1−02=1 1=1−3π2+4n=1∑∞n2(−1)n+1(−π≤x≤π) n=1∑∞n2(−1)n+1=12π2
1.3 函数、函数的傅里叶级数展开、傅里叶级数的和函数之间的关系的分析
作图过程如下:

函数 f ( x ) = 1 − x 2 ( 0 ≤ x ≤ π ) f(x)=1-x^2(0\leq x\leq \pi) f(x)=1−x2(0≤x≤π)

余弦级数中的部分余弦波
a n cos n x a_n\cos nx ancosnx
此图中 n n n只从1取到5,共5个余弦波

各个余弦波(绿色)叠加后形成余弦级数(橙色)
∑ n = 1 ∞ a n cos n x \sum\limits_{n=1}^{\infty}a_n\cos nx n=1∑∞ancosnx

余弦级数加 a 0 / 2 a_0/2 a0/2 的图像(蓝色)
a 0 2 + ∑ n = 1 ∞ a n cos n x \frac{a_0}{2}+\sum\limits_{n=1}^{\infty}a_n\cos nx 2a0+n=1∑∞ancosnx

函数 f ( x ) f(x) f(x)(红色)及将其展开成余弦形式的傅里叶级数的图像(蓝色)

上图中红色为函数、蓝色为函数的傅里叶级数展开、函数与函数的傅里叶级数展开重合部分为和函数,超过收敛域的部分函数与傅里叶级数的和函数不再相等
当n从1取得30时,傅里叶级数的和函数基本与函数完全吻合!!

作图过程总览
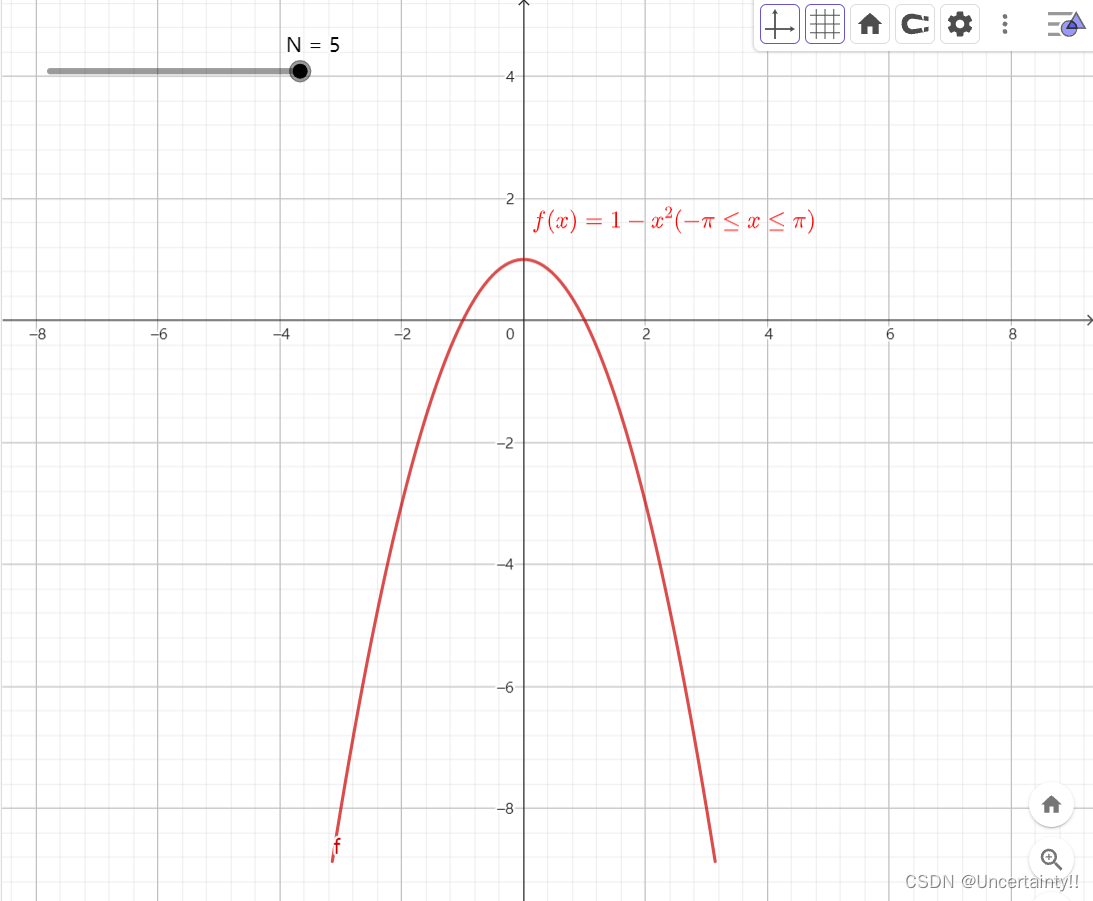 f(x) f(x) |  a_ncos(nx) a_ncos(nx) |
 余弦级数 余弦级数 |  函数及其余弦级数 函数及其余弦级数 |


![[React] 性能优化相关 (二)](http://pic.xiahunao.cn/[React] 性能优化相关 (二))



 | 包的使用)




)







