多目标平衡优化器黏菌算法(MOEOSMA)求解CEC2020多模式多目标优化

多目标平衡优化器黏菌算法（MOEOSMA）比现有的多目标黏菌算法具有更好的优化性能。在MOEOSMA中，动态系数用于调整勘探和开采趋势。采用精英存档机制来促进算法的收敛性。使用拥挤距离法来保持Pareto前沿的分布。采用平衡池策略模拟黏菌的协同觅食行为，有助于提高算法的探索能力。求解最新的CEC2020函数。

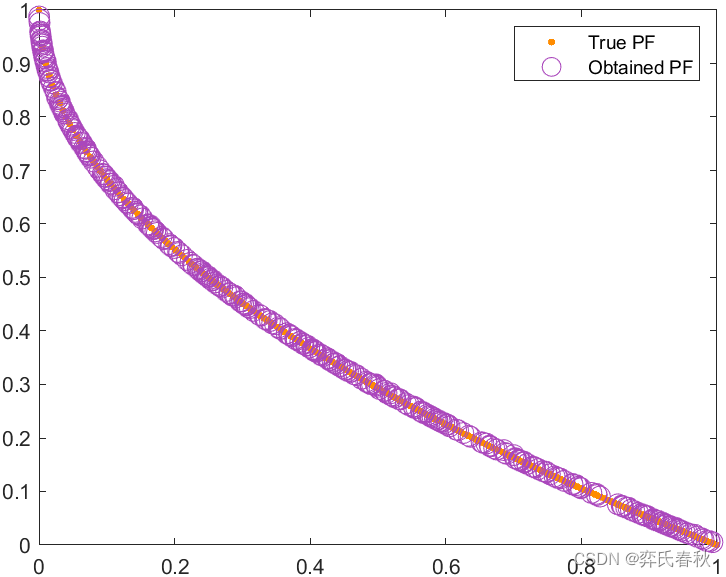
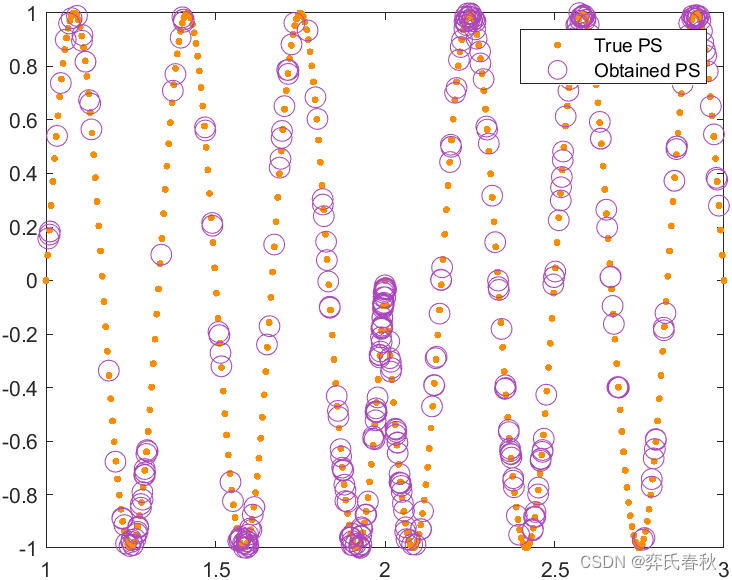
为了验证所提出的MOEOSMA的有效性，使用CEC2020函数来分析算法在目标空间和决策空间中的收敛行为。与以前的测试套件不同，CEC2020不仅包括每个测试问题的真实PF，还包括相关的局部和全局PS，使研究人员能够评估算法在目标空间和决策空间中的性能。由于CEC2020函数包含多个全局最优PS，因此算法在目标空间中的良好性能并不意味着可以找到多个全局优化PS。决策空间（IGDX）和目标空间（IGDF）中的IGD（Zhang等人，2008）分别用于评估获得的PS和PF的质量。在决策空间中，IGDX值越小，所获得的PS就越接近真实PS。在目标空间中，IGDF值越小。所获得的PF就越接近真正的PF。

1 CEC 2020多模式多目标优化特别会议的问题定义和评估标准：

在多目标优化问题中，可能存在两个或多个全局或局部帕累托最优集（PS），其中一些可能对应于相同的帕累托前沿（PF）。这些问题被定义为多模态多目标优化问题（MMOPs）。可以说，找到这些多个PS中的一个可能足以获得一些问题的可接受的解决方案。然而，未能识别多个PS可能会阻止决策者考虑可以提高性能的解决方案选项。最近，许多研究人员提出了不同的多模式多目标优化（MMO）算法。在CEC’2020的MMO测试套件中，设计了一组具有不同特征的MMO试验问题，如具有不同形状的PS和PF的问题、局部和全局PS共存的问题、PS的可扩展数量、决策变量和目标。此外，给出了一个公平、适当的评估标准和参考数据，以评估不同MMO算法的性能。

1.1 相关定义：

如果一个解不受任何其他解支配，则称为非支配解。非支配解集称为帕累托最优集（PS）。目标空间中与PS相对应的向量集称为Pareto前沿（PF）。

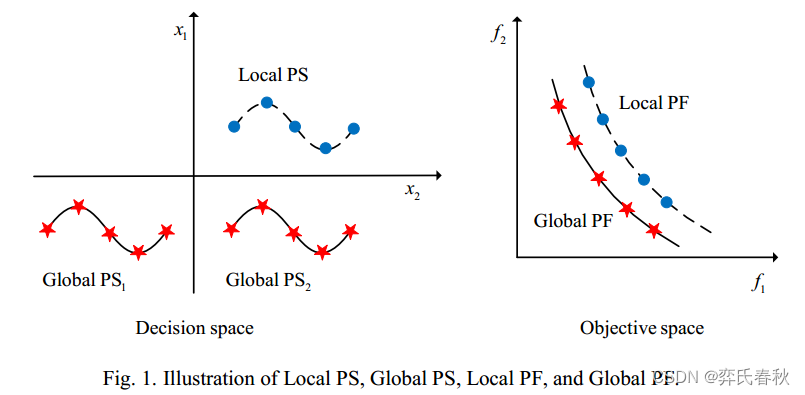
全局帕累托最优集（Global PS）：对于解集GP中的任意解，如果不存在支配该集GP中任何解的解，则称GP为全局帕累托优集。

全局Pareto Front（Global PF）：目标空间中与全局PS相对应的所有向量的集合被定义为全局Pareto Front。

局部Pareto最优集（局部PS）：对于任意解 $eq?%5Cvec%7Bx%7D$ 在解集 $eq?P_%7BL%7D$ 中，如果不存在邻域解 $eq?%5Cvec%7By%7D$ 满足 $eq?%5Cleft%20%5C%7C%20%5Cvec%7By%7D-%5Cvec%7Bx%7D%20%5Cright%20%5C%7C_%7B%5Cinfty%20%7D%5Cleq%20%5Csigma$ （ $eq?%5Csigma$ 是一个小正值），支配集合 $eq?P_%7BL%7D$ 中的任何解，则 $eq?P_%7BL%7D$ 称为局部Pareto最优集；

局部Pareto Front（局部PF）：目标空间中与局部PS相对应的所有向量的集合被定义为局部Pareto Front。

给出了判断给定多目标优化问题是否为MMO问题的方法。对于多目标优化问题，如果它满足以下条件之一，则它是MMO问题：

1）它至少有一个局部Pareto最优解；

2）它至少有两个全局Pareto最优解对应于PF上的同一点。

不受任何邻域解支配的解称为局部Pareto最优解。在可行空间中不受任何解支配的解称为全局Pareto最优解。

图1显示了具有两个全局PS和一个局部PS的双目标最小化问题。带星形的实线表示全局PS/PF，而带圆点的虚线表示局部PS/PF。注意，一个多模态多目标问题可能有几个局部PS和全局PS。

1.2 MOEOSMA求解CEC2020多模式多目标函数

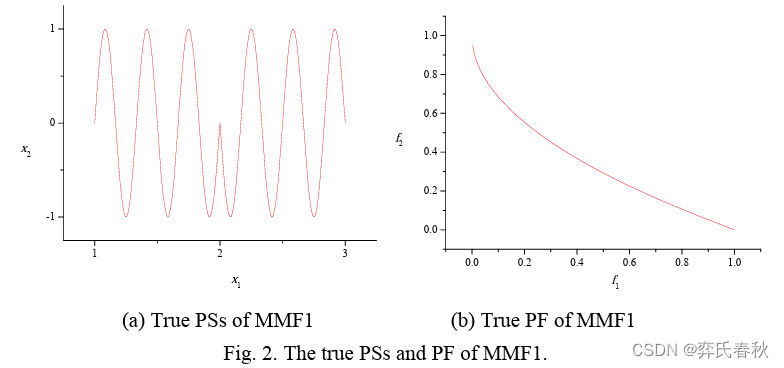
MMF1：

MMF5:

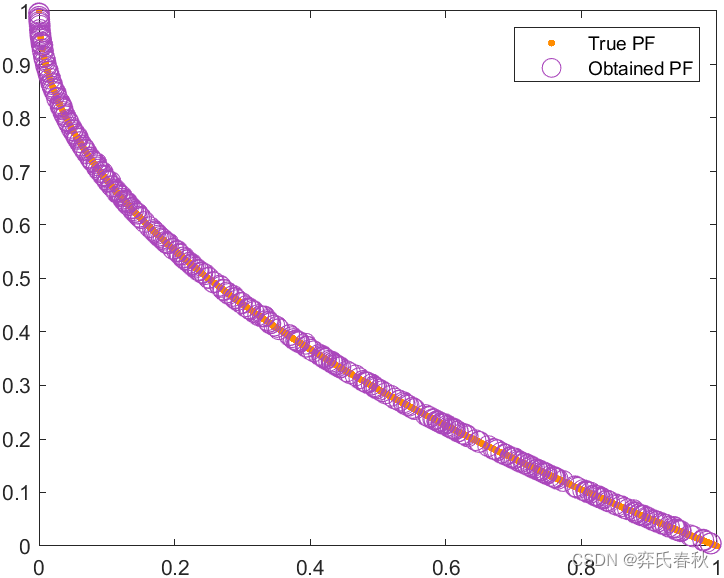
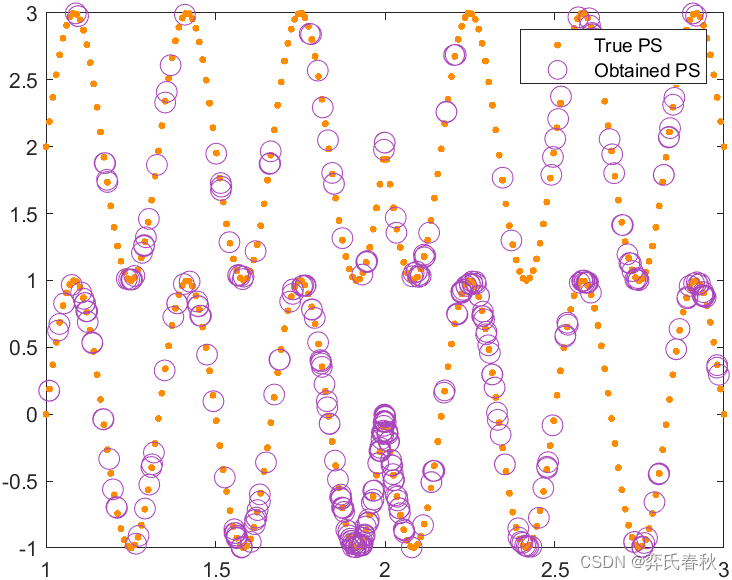
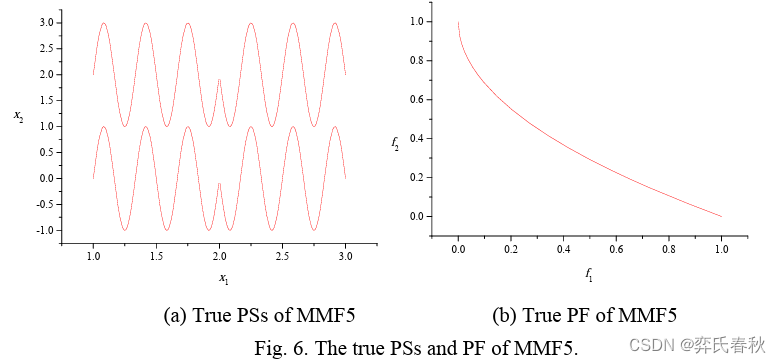
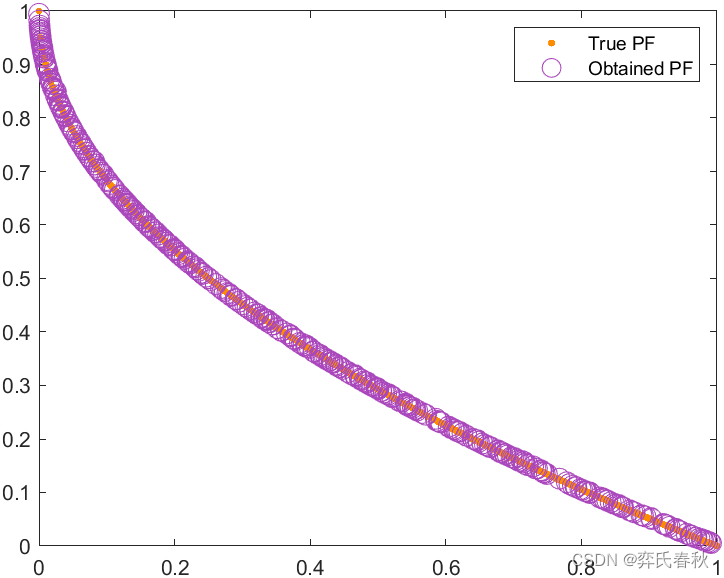
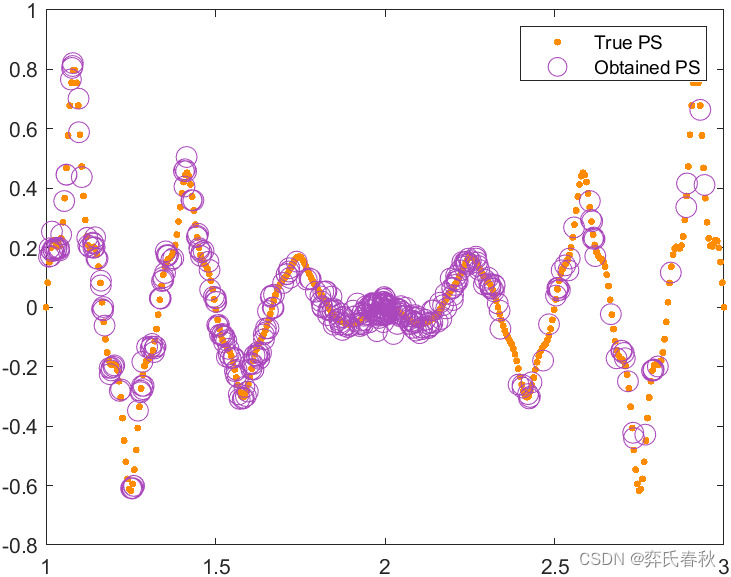
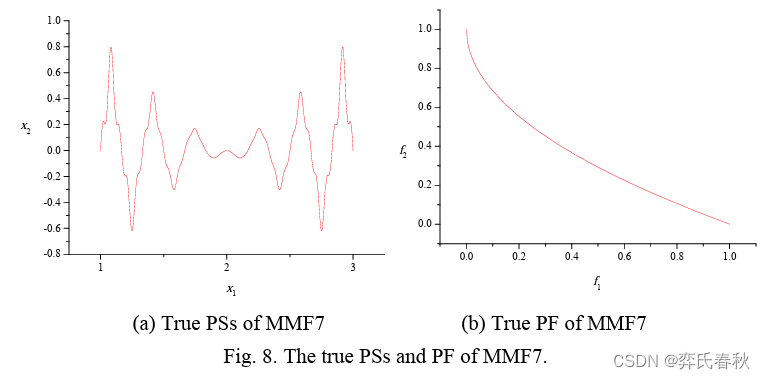
MMF7：

function [fname,xl,xu,n_obj,n_var,repoint,N_ops] = func_info(Func_num)
% func_info: input the number of CEC2020 function and return the information about the corresponding function
switch Func_numcase 1fname='MMF1';      % function namen_obj=2;           % the dimensions of the decision spacen_var=2;           % the dimensions of the objective spacexl=[1 -1];         % the low bounds of the decision variablesxu=[3 1];          % the up bounds of the decision variablesrepoint=[1.1,1.1]; % reference point used to calculate the hypervolume, it is set to 1.1*(max value of f_i)N_ops=2;           % the number of global PS and local PScase 2fname='MMF2';n_obj=2;n_var=2;xl=[0 0];xu=[1 2];repoint=[1.1,1.1];N_ops=2;.
.
.
.case 23fname='MMF16_l2';  % function namen_obj=3;n_var=3;xl=[0 0 0];xu=[1 1 1];repoint=[2.5,2.5,2.5];N_ops=3;case 24fname='MMF16_l3';  % function namen_obj=3;n_var=3;xl=[0 0 0];xu=[1 1 1];repoint=[2.5,2.5,2.5];N_ops=4;
end
end

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/93118.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！