目录

一、最大子段和

1、什么是最大子段和

2、暴力枚举

3、分治法

4、动态规划

二、最长公共子序列

1、什么是最长公共子序列

2、暴力枚举法

3、动态规划法

4、完整代码 

---

 

一、最大子段和

1、什么是最大子段和

        子段和就是数组中任意连续的一段序列的和，而最大子段和就是寻找子段和里最大的一个值。下面的解释中S[l,r]会用来表示l到r的子段和，l和r分别表示左值和右值。

        最大子段和一般有三种解决方案：暴力枚举法，分治法，动态规划法。下面将逐个介绍。

2、暴力枚举

        暴力枚举就是遍历所有的子段和，寻找最大的子段和，时间复杂度 。相对无脑，直接贴上代码。

    //暴力枚举法public static int maxsize_violate(ArrayList<Integer>arr,int left, int right){int max=-99999999;for(int i=left;i<=right;i++){int sum=0;for(int j=i;j<=right;j++){for(int k=i;k<=j;k++){sum+=arr.get(k);  //最大值来源}if(sum>max)max=sum;sum=0;}}return max;}

3、分治法

        将每个问题分解为三个小问题，左一半的子段和，右一半的子段和，（必须）跨区域的子段和。

        伪代码如下，可以看到左子段和与右子段和都是递归求解（3、4），跨区域的一定是左右两个子段和最大值的和（5、6、7），最后选择左子段和、右子段和、跨域子段和中最大的子段和（8、9）。

        完整代码：

    //分治法public static int maxsize(ArrayList<Integer>arr, int left, int right){int sum=0,midSum=0,leftSum=0,rightSum=0;int center,s1,s2,lefts,rights;//左右相等，返回左值if (left==right){    sum=arr.get(left);}//否则，分治法else {center=(left+right)/2;leftSum=maxsize(arr,left,center);         //left，l+r/2     //左区间最大值rightSum=maxsize(arr,center+1,right);     //l+r/2+1，right  //右区间最大值//后面都是在计算跨区域最大值（必须跨区域），一定是左区间贴近边界的最大值加右区间贴近边界的最大值相加。s1=0;lefts=0;                             //s1存左侧区间最大值，lefts作为tempfor (int i=center;i>=left;i--){lefts+=arr.get(i);if (lefts>s1){s1=lefts;}}s2=0;rights=0;                             //s2存右侧区间最大值，rights作为temp               for (int j=center+1;j<=right;j++){rights+=arr.get(j);if (rights>s2){s2=rights;}}midSum=s1+s2;                              //中间跨域的等于左侧加右侧的if (midSum<leftSum){sum=leftSum;}else {sum=midSum;}if (sum<rightSum){sum=rightSum;}}return sum;}

4、动态规划

        动态规划法是自底向上推导，假设为第i个数，为包含最后一个数的连续子段和，sum为最大子段和。

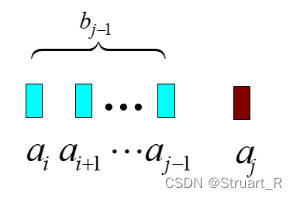
        建立于下面图这个关系，假设已经有到的子段和,那么加入后一个生成只有两种可能：

（1）,那么

（2）,那么

        对于的每一个，都要与sum取最大值，保证sum为到中最大的值，返回sum。

        完整代码： 

    //动态规划法public static int maxsum(ArrayList<Integer>arr, int n){int sum=-999999;int b=0;for(int i=0;i<=n;i++){if(b>0)b+=arr.get(i);else    b=arr.get(i);if(b>sum)sum=b;}return sum;}

二、最长公共子序列

1、什么是最长公共子序列

        子序列是指序列中任意不一定连续但顺序的若干个字符组成的序列。如下图中Z1={B,C,A}为X的子序列，B,C,A三个字符在X中顺序出现，且不一定连续。

        公共子序列就是指两个序列之间存在一个共同的子序列，而我们就是要找到最长的一个公共子序列。

2、暴力枚举法

        暴力枚举法，不仅占用了相当大的内存存放所有子序列，和所有公共子序列，而且浪费了巨大的时间，时间复杂度指数级。

3、动态规划法

        动态规划法仍然是这种自底向上的算法，讨论前一项的最长公共子序列通过比较两个序列下一个值，判定是否进入子序列。动态规划法的时间复杂度为O（mn）。

        使用c[i][j]数组记录和的最长公共子序列长度， b[i][j]数组记录子序列的产生情况。c数组存在下面的递归结构成立，与b数组的关系如下，根据这个递推式，可以写出c和b数组的生成函数。

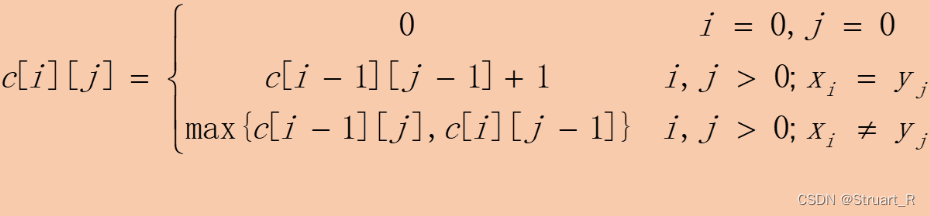
c[i][j]=c[i-1][j-1]+1	b[i][j]=1	↖
c[i][j]=c[i-1][j]	b[i][j]=2	↑
c[i][j]=c[i][j-1]	b[i][j]=3	←

 

如何构造最长子序列？

         就是根据b数组的指引，倒推子序列，所有b[i][j]=1，也就是b数组指引为左上箭头的，都是公共序列的值，将他们按顺序串接就得到了最大子序列。

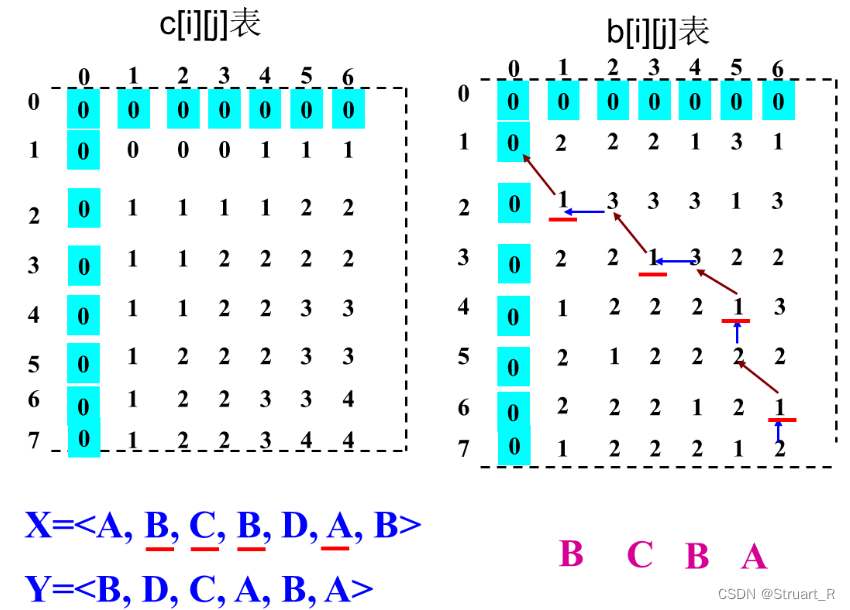
        注意一个问题，X序列是y轴方向的，Y序列是x轴方向的。 

4、完整代码

//最长公共子序列
import java.util.Scanner;
public class LCS {public static void main(String [] args){String x=new Scanner(System.in).nextLine();String y=new Scanner(System.in).nextLine();int m=x.length();int n=y.length();int [][]c=new int[m+1][n+1];int [][]b=new int[m+1][n+1];LCSLength(x, y, c, b);for(int i=0;i<m+1;i++){for(int j=0;j<n+1;j++){System.out.print(c[i][j]);System.out.print("\t");}System.out.println("");}BuildLCS(m,n,x,b);}//最长公共子序列生成c和b数组public static void LCSLength(String x,String y,int [][]c,int [][]b){int i,j;int m=x.length();int n=y.length();for(i=0;i<m+1;i++)c[i][0]=0;for(i=0;i<n+1;i++)c[0][i]=0;for(i=1;i<m+1;i++){for(j=1;j<n+1;j++){if(x.charAt(i-1)==y.charAt(j-1)){c[i][j]=c[i-1][j-1]+1;b[i][j]=1;}else if(c[i-1][j]>=c[i][j-1]){c[i][j]=c[i-1][j];b[i][j]=2;}else{c[i][j]=c[i][j-1];b[i][j]=3;}}}}//构造最长公共子序列public static void BuildLCS(int i,int j,String x,int[][]b){if(i==0|j==0){return;}if(b[i][j]==1){BuildLCS(i-1, j-1, x, b);System.out.print(x.charAt(i-1));}else if(b[i][j]==2){BuildLCS(i-1,j,x,b);}else{    BuildLCS(i, j-1, x, b);}}
}